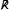Number Forms and Mathematical Symbols

Numbers

Symbol	Code
𝟬	<s:zerobold>
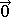	<s:0arrow>
	<s:0arrowbold>
	<s:0vecbold>
	<s:0hat>
½	<s:frac12>
¼	<s:frac14>
¾	<s:frac34>
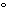	<s:naught>
⁰	<s:naught_hi>
₀	<s:naught_lo>
Ⅰ	<s:roman1>
Ⅹ	<s:roman10>
Ⅽ	<s:roman100>
Ⅿ	<s:roman1000>
ⅿ	<s:roman1000_sm>
ⅽ	<s:roman100_sm>
ⅹ	<s:roman10_sm>
ⅺ	<s:roman11_sm>
ⅻ	<s:roman12_sm>
ⅰ	<s:roman1_sm>
Ⅱ	<s:roman2>
ⅱ	<s:roman2_sm>
Ⅲ	<s:roman3>
ⅲ	<s:roman3_sm>
Ⅳ	<s:roman4>
ⅳ	<s:roman4_sm>
Ⅴ	<s:roman5>
Ⅼ	<s:roman50>
Ⅾ	<s:roman500>
ⅾ	<s:roman500_sm>
ⅼ	<s:roman50_sm>
ⅴ	<s:roman5_sm>
Ⅵ	<s:roman6>
ⅵ	<s:roman6_sm>
Ⅶ	<s:roman7>
ⅶ	<s:roman7_sm>
Ⅷ	<s:roman8>
ⅷ	<s:roman8_sm>
Ⅸ	<s:roman9>
ⅸ	<s:roman9_sm>
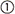	<s:circle1>
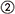	<s:circle2>
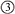	<s:circle3>
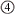	<s:circle4>
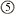	<s:circle5>
½	<s:half>
₀	<s:sub0>
₁	<s:sub1>
₂	<s:sub2>
₃	<s:sub3>
₄	<s:sub4>
₅	<s:sub5>
₆	<s:sub6>
₇	<s:sub7>
₈	<s:sub8>
₉	<s:sub9>
⁰	<s:sup0>
¹	<s:sup1>
²	<s:sup2>
³	<s:sup3>
⁴	<s:sup4>
⁵	<s:sup5>

Math

Symbol	Code
≊	<s:almostequal_equal>
≅	<s:approximate>
⊦	<s:assertion>
∵	<s:because>
⇔	<s:bicond>
⋈	<s:bowtie_op>
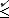	<s:checklteq>
∁	<s:complement>
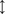	<s:correspondence>
≘	<s:corresponds>
≏	<s:difference>
≐	<s:doteq>
″	<s:doubleprime>
⊤	<s:downtack>
∎	<s:end_proof>
≌	<s:equal_all>
≑	<s:equal_geom>
⋝	<s:equal_greater>
⋜	<s:equal_less>
⋞	<s:equal_precedes>
⋟	<s:equal_succeeds>
≚	<s:equiangular>
⇌	<s:equilarrow>
≎	<s:equiv_geom>
≣	<s:equiv_strict>
≍	<s:equiv_to>
℮	<s:estimated>
≙	<s:estimates>
ℇ	<s:euler>
∃	<s:exists>
∀	<s:forall>
⊩	<s:forces>
∜	<s:fourthroot>
⁄	<s:fracslash>
⁄	<s:frasl>
›	<s:greaterthan_rq>
	<s:greenmultiply>
≡	<s:identical>
⇒	<s:implies>
∆	<s:increment>
⊺	<s:intercalate>
⊣	<s:lefttack>
‹	<s:lessthan_lq>
∡	<s:measuredangle>
⊧	<s:models>
⊼	<s:nand>
⋀	<s:nary_and>
∐	<s:nary_coproduct>
⋂	<s:nary_intersect>
∏	<s:nary_product>
∑	<s:nary_summation>
≇	<s:neither_approx>
⊽	<s:nor>
⊲	<s:norm_subgr>
⊴	<s:norm_subgr_equal>
¬	<s:not>
≉	<s:not_almostequal>
≆	<s:not_approx>
≄	<s:not_asymptotic>
∄	<s:not_exists>
⊮	<s:not_forces>
≯	<s:not_greater>
≢	<s:not_identical>
≮	<s:not_less>
∦	<s:not_parallel>
⊀	<s:not_precedes>
⊬	<s:not_proves>
⊁	<s:not_succeeds>
⊭	<s:not_true>
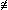	<s:notcongruent>
∤	<s:notdivides>
≠	<s:notequal>
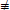	<s:notequiv>
≯	<s:notgreater>
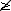	<s:notgreaterorequal>
≱	<s:notgreaterorequal2>
≮	<s:notless>
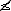	<s:notlessorequal>
≰	<s:notlessorequal2>
	<s:notmuchgreater>
	<s:notmuchless>
	<s:notrelated>
%	<s:percent>
≺	<s:precedes>
≼	<s:precedes_equal>
≾	<s:precedes_equiv>
⊰	<s:precedes_rel>
′	<s:prime>
∷	<s:proportion>
∝	<s:propto>
	<s:redmultiply>
±	<s:redplusminus>
⊢	<s:righttack>
⊾	<s:rt_angle_arc>
⋋	<s:semiprod_lf>
⋉	<s:semiprod_lf_norm>
⋌	<s:semiprod_rt>
⋊	<s:semiprod_rt_norm>
⊳	<s:subgr_norm_contains>
⊵	<s:subgr_norm_contains_equal>
≻	<s:succeeds>
≽	<s:succeeds_equal>
≿	<s:succeeds_equiv>
⊱	<s:succeeds_rel>
∴	<s:therefore_sm>
⁻	<s:supminus>
⁺	<s:supplus>
˜	<s:tilde_sm>
≋	<s:tilde_trp>
⊨	<s:true>
⊻	<s:xor>
∧	<s:and>
∠	<s:angle>
≈	<s:approx>
≃	<s:asymptotic>
/	<s:bigdiv>
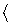	<s:bra>
⟨	<s:bra_acc>
⊖	<s:circleminus>
⊕	<s:circleplus>
⊜	<s:circleequals>
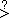	<s:ckgreater>
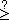	<s:ckgreaterequal>
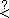	<s:ckless>
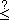	<s:cklessequal>
≟	<s:ckequal>
∘	<s:compose>
≌	<s:congruent>
⨯	<s:cross>
÷	<s:divide>
≟	<s:eqq>
≡	<s:equivalent>
≥	<s:greaterorequal>
>	<s:greaterthan>
∞	<s:infinity>
	<s:infinitysm>
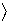	<s:ket>
⟩	<s:ket_acc>
⌈	<s:lceiling>
[[	<s:leftgrint>
≤	<s:lessorequal>
<	<s:lessthan>
⌊	<s:lfloor>
−	<s:minus>
∓	<s:minusplus>
≫	<s:muchgreaterthan>
≪	<s:muchlessthan>
✕	<s:multiply>
∨	<s:or>
⊥	<s:orthogonal>
∥	<s:parallel>
▰	<s:parallel_black>
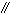	<s:parallel_s>
▱	<s:parallel_white>
±	<s:plusminus>
⌉	<s:rceiling>
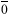	<s:repzero>
⌋	<s:rfloor>
∟	<s:rightangle>
]]	<s:rightgrint>
√	<s:sqrt>
√	<s:square_root>
	<s:squareminus>
	<s:squareplus>
∃	<s:thereexists>
∴	<s:therefore>
×	<s:times>
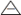	<s:triangleminus>
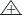	<s:triangleplus>
≻	<s:strictpref>
‴	<s:tripleprime>
≿	<s:weakpref>

Sets

Symbol	Code
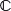	<s:complex>
∋	<s:contains>
∈	<s:element>
ℤ	<s:integers>
∩	<s:intersect>
⋁	<s:nary_or>
⋃	<s:nary_union>
∌	<s:not_contains>
∉	<s:not_element>
⊄	<s:not_subset>
⊈	<s:not_subset_neq>
⊅	<s:not_superset>
⊉	<s:not_supersetneq>
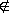	<s:notin>
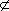	<s:notsubset>
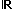	<s:Reals>
ℝ	<s:Reals2>
⊃	<s:superset>
⊇	<s:superseteq>
⊋	<s:supersetneq>
∪	<s:union>
∅	<s:empty_set>
⊂	<s:subset>
⊆	<s:subseteq>
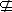	<s:subsetneq>
⊊	<s:subset_neq>

Vectors

Symbol	Code
↿	<s:leftupvector>
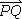	<s:PQvecitalic>
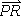	<s:PRvecitalic>
⇂	<s:rightdownvector>
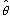	<s:vecthetahat>
‹	<s:vecstart>
›	<s:vecstop>

Calculus

Symbol	Code
⌡	<s:bottomintegral>
∮	<s:contourintegral>
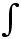	<s:intbig>
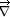	<s:nablaarrow>
∂	<s:partial>
∯	<s:surfaceintegral>
⌠	<s:topintegral>
∰	<s:volumeintegral>
∬	<s:doubleintegral>
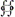	<s:doublelineint>
∫	<s:integral>
∳	<s:integral_anti_cont>
∱	<s:integral_clock>
∲	<s:integral_clock_cont>
∇	<s:nabla>
∭	<s:tripleintegral>
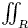	<s:doubleint_r>
	<s:fprimex_acc>
	<s:fx_acc>
	<s:gprimex_acc>
	<s:gx_acc>
	<s:hprimex_acc>
	<s:hx_acc>
	<s:lineint>
	<s:ointccw>
	<s:ointccw1>
	<s:ointccw2>
	<s:ointcw>