Lab 9: Optimization Problems

The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.

After you learn how to find the extrema of a function in calculus, you will be asked to do application problems involving absolute maxima and minima. The next few examples will help with some of the concepts needed in order to solve the calculus optimization problems. In optimization problems in calculus, you will have 2 equations, an objective function, which is the one that needs to be maximized or minimized, and a constraint equation, which is one that is used to put the objective function in terms of one variable. You may want to refer back to Lab 6 for some of the geometric formulas.

Often, an optimization problem will want you to minimize the cost of building something, such as a fence or a box. Let's discuss how to calculate the cost of making an object if you know the cost of the materials.

Example 9.1:

Suppose you want to fence a rectangular pasture (pictured below) and the cost of the fence is $10/foot.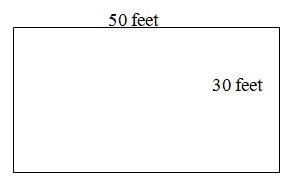

Since we want to fence in the entire pasture, we will need $2 \cdot (50 \text{ feet}) + 2 \cdot (30 \text{ feet}) = 160 \text{ feet}$ of fence. To find the cost of the fence, we will have $\text{Cost} = \text{ Cost per foot } \cdot \text{ Total number of feet}$. Using this formula, we get

$\text{Cost of fence } = \frac{\$10}{\text{foot}} \times 160 \text{ feet} = \$1,600$.

What if you are told that the longer sides of the fence cost \$12 per foot and the shorter sides cost $10 per foot? Then you would have

$\text{Cost of fence } = \frac{\$12}{\text{foot}} \times 2 \cdot (50 \text{ feet}) + \frac{\$10}{\text{foot}} \times 2 \cdot (30 \text{ feet}) = \$1,800$.

Example 9.2:

A rectangular storage container with a closed top is to have a volume of 24 m³. The length of its base is twice the width. Material for the top and the base costs \$9 per square meter. Material for the sides costs \$8 per square meter. Find the cost of materials for the cheapest such container. (Note: In this problem, minimizing the surface area is not the same as minimizing the cost!)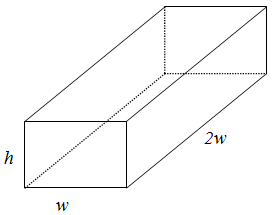

In the diagram, the width of the base is represented by w and since the length of the base is twice the width, the length is labeled as 2w, and the height of the box is given by h. In order to write the objective function, we need to read carefully and figure out what needs to be maximized or minimized. It looks like we need to minimize the cost of the box. Thus we need to write an equation for cost,

$\text{Cost}$	$ \;=\; 2$	$(9 \cdot 2w \cdot w)$	$\;+\; 2$	$(8 \cdot h \cdot w)$	$\;+\; 2$	$(8 \cdot h \cdot 2w)$.
The 2 in front of each cost takes into account that there are two of each of the sides.		Cost of bottom		Cost of front		Cost of one side

If we simplify this equation a bit, we get $\text{Cost} = 36w^{2} + 16hw + 32hw = 36w^{2} + 48hw$. Thus, we have our objective function, but it is an equation of two variables so we need to figure out the constraint equation so that we can eliminate one of the variables. What other information are we given in the problem? We were given a fixed volume for the box, so using the formula for the volume of a rectangular prism, we would have that $V = w \cdot 2w \cdot h = 2w^2h$. Since we know that the fixed volume is 24 cubic meters, our constraint equation is $2w^2h = 24$. Since we need to minimize the objective function, we need to have it as a function of one variable, instead of two. Should we solve the secondary equation for h or w? It would appear that h would be a better choice. We have that $h = \frac{12}{w^{2} }$ and then if we replace that for h in the cost equation, we get that $C = 36w^{2} + 48\left(\frac{12}{w^{2}}\right)w$.

Then we would simplify this function before taking the derivative to solve the calculus problem. In lab, we do not solve the calculus problem, we just focus on getting the objective function in terms of one variable.

Example 9.3:

A poster is to have an area of 54 in², with 1-inch margins on top and bottom, and 1 ½-inch margins on the sides. Find the dimensions of the poster that will allow the largest printed area.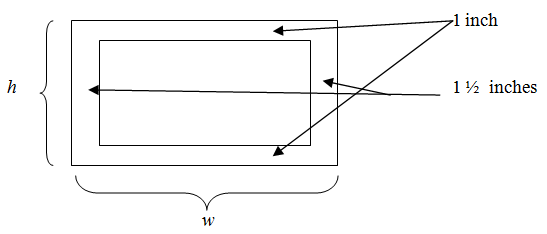

In the diagram, the height of the poster is represented by h and the width by w. The inside rectangle represents the printed area of the poster, which is the quantity that needs to be maximized so we need to find an equation that represents the area of this inside rectangle. Since we were given the margins for the poster, the printed area height should be 2 inches smaller than the height of the poster, $h - 2$.

The width of the printed area will be 3 inches smaller than the width of the poster, $w - 3$. Therefore, the objective function is $A = (h - 2)(w - 3)$. Now we need to find a constraint equation so that we can eliminate one of the variables in the objective function. In the problem, we were told that the area of the poster is 54 square inches. Thus, our constraint equation is $h \cdot w = 54$. Solving for w and substituting into the objective function can give you that $A = (h - 2)\left(\frac{54}{h} - 3\right)$. This is the equation that needs to be simplified before solving the calculus problem.