Lab 2: The Difference Quotient
The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.
One important use of combining functions in calculus is simplifying the difference quotient for a function f.
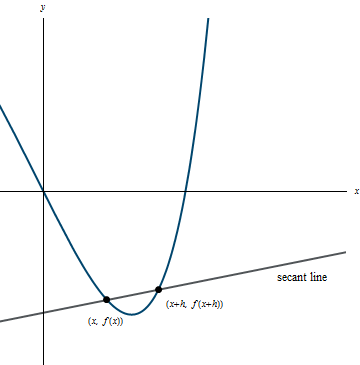
The difference quotient for f is defined as \frac{f(x \,+\, h) \,-\, f(x)}{h}. This represents the slope of the secant line of the curve y = f(x), through the points (x,\, f(x)) and (x + h,\, f(x + h)). Normally h is small with respect to x. We shall denote the secant line pictured in Figure 2.1 by Sl(x,\, h). Recall that the slope of the line is represented by the change in y divided by the change in x. In Figure 2.1, we find the slope of the secant line by evaluating m = \frac{\Delta y}{\Delta x} = \frac{f(x \,+\, h) \,-\, f(x)}{(x \,+\, h) \,-\, x} = \frac{f(x \,+\, h) \,-\, f(x)}{h}.
Understanding the difference quotient is vital in the study of calculus.
Figure 2.1
Example 2.1:
Simplify the difference quotient for f(x) = \frac{2}{x}.| \frac{f(x \,+\, h) \,-\, f(x)}{h} | = | \dfrac{\frac{2}{x \,+\, h} \,-\, \frac{2}{x}}{h} | First, we plug the function into the formula for the difference quotient. | |
| = | \dfrac{\frac{2x \,-\, 2(x \,+\, h)}{x(x \,+\, h)}}{h} | Then we get a common denominator in the numerator of the fraction. | ||
| = | \dfrac{\frac{2x \,-\, 2x \,-\, 2h}{x(x \,+\, h)}}{h} | Then we distribute and simplify the numerator of the numerator. | ||
| = | \dfrac{\frac{-2h}{x(x \,+\, h)}}{\frac{h}{1}} | |||
| = | \frac{-2h}{x(x \,+\, h)} \cdot \frac{1}{h} | When dividing by a fraction, we multiply by the reciprocal of the fraction in the denominator. | ||
| = | \frac{-2}{x(x \,+\, h)} |
Sometimes the slope of the secant line is given in a different form: m = \frac{f(a \,+\, h) \,-\, f(a)}{h}, where a is a specific x-value given in the problem. This form is used when trying to find the slope of the secant line through a specific point, (a,\, f(a)) and the nearby point (a \,+\, h,\, f(a \,+\, h)).
Example 2.2:
Find the slope of the secant line (using the second form) for the function f(x) = x^2 when a = 4. When a = 4, f(4) = 16 so we are looking for the slope of the secant line through the point (4,\, 16) and (4 \,+\,h,\, (4 \,+\, h)^2).| m | = | \frac{f(a \,+\, h) \,-\, f(a)}{h} | We use the formula for the slope of the secant line. | |
| = | \frac{f(4 \,+\, h) \,-\, f(4)}{h} | In this example, a = 4 so we substitute into the slope formula. | ||
| = | \frac{(4 \,+\, h)^2 \,-\, 16}{h} | Now we plug the function into the formula. | ||
| = | \frac{16 \,+\, 8h \,+\, h^2 \,-\, 16}{h} | Then we perform the algebraic operations and simplify. | ||
| = | \frac{8h \,+\, h^2}{h} | |||
| = | \frac{h(8 \,+\, h)}{h} = 8 + h | |||