Lab 8: Solving Various Types of Inequalities
The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.
In calculus you will learn that the derivatives can give you lots of information about the function and its graph. In this lab, we will focus on the algebra and trigonometry needed to help you extract this information. In order to do this, we need to be able to solve equations (Lab 7) and solve inequalities, which we will cover here.
Example 8.1:
Solve the inequality $x^2 - 5x - 24 \geq 0$.Before we can solve the inequality, we must solve the equation. Therefore, the first step in the solution process is to solve the equation $x^2 - 5x - 24 = 0$. The solution for this equation is given by the following.
Once you know when the expression equals zero, then you need to determine what happens with the expression for the other values of x in the domain of the function. We were asked to find out when the expression was greater than or equal to zero. We know that it equals zero when $x = 8$ and $x = -3$, but we need to determine when the expression is positive. There are a couple of different methods of determining when an expression is positive or negative. We will demonstrate both of them in this example. Both methods utilize the fact that the x-axis represents the set of all real numbers.
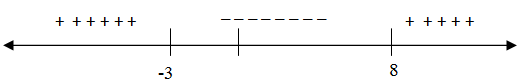
You can see that these two x-values split the number line into three sections. To figure out what is happening with our expression for other values of x, we need to pick test points in each section of the number line.
| If $x = -4$, then $(x - 8)(x + 3)$ | $=$ | $(-4 - 8)(-4 + 3)$ |
| $=$ | $(-12)(-1) = 12$. |
Since 12 is a positive number, our expression is positive so we put positive signs above that section of the number line.
| If $x = 0$, then $(x - 8)(x + 3)$ | $=$ | $(0 - 8)(0 + 3)$ |
| $=$ | $(-8)(3) = -24$. |
Since −24 is a negative, our expression is negative so we put negative signs above that section of the number line.
| If $x = 9$, then $(x - 8)(x + 3)$ | $=$ | $(9 - 8)(9 + 3)$ |
| $=$ | $(1)(12) = 12$. |
Since 12 is a positive number, our expression is positive so we put positive signs above that section of the number line.
Now we have enough information to solve the inequality. We were to find all x-values where the expression was greater than or equal to zero. Therefore, our solution set is $\{x | x \leq -3 \text{ or } x \geq 8\}$, or in interval notation, $(-\infty, -3] \cup [8, \infty)$.
The other method that will be demonstrated is very similar but uses a table instead of a number line. You will need to decide which method works best for you, but the number line will be used throughout this lab.
Once we have determined that the expression is 0 when $x = 8$ or when $x = -3$, then we create the following type of table.
| Interval | $(-\infty, -3)$ | $(-3, 8)$ | $(8, \infty)$ |
|---|---|---|---|
| Test Value | $-4$ | $0$ | $9$ |
| $(x - 8)$ | $-12 \;(-)$ | $-8 \;(-)$ | $1 \;(+)$ |
| $(x + 3)$ | $-1 \;(-)$ | $3 \;(+)$ | $12 \;(+)$ |
| $(x - 8)(x + 3)$ | $12 \;(+)$ | $-24 \;(-)$ | $12 \;(+)$ |
| Conclusion | $\text{positive}$ | $\text{negative}$ | $\text{positive}$ |
The solution set will be the same, but don't forget that the original problem asked when the expression was greater than or equal to zero so you need to include −3 and 8 in the intervals.
In either of the above methods, we do not really care what the numerical value of the expression is for the selected test value. We really only care if the test value yields a positive or negative number when entered into the expression. In the second method, you might see positive signs or negative signs in the table rather than actual numbers.
A simpler way to approach the problem that we were given would be to think about it graphically. We know that $f(x) = x^2 - 5x - 24$ is a parabola that opens upward. By visualizing the graph, we can see that the graph is above the x-axis (greater than zero) for x-values at the tails of the curve. This function would be greater than or equal to zero as x gets really small $(-\infty)$ or really large $(+\infty)$.
In Calculus I, you will encounter these types of problems when you are asked to determine where a function is increasing or decreasing. Often, the functions will be more complicated so let's now look at some complicated examples. So far in calculus your instructor may have not had you simplify your derivatives, but now if we are trying to determine where the function is increasing (first derivative is positive) or decreasing (first derivative is negative), we must first simplify the derivatives. Now would be a good time to review simplifying algebraic expressions from Lab 4.
Example 8.2:
Determine the x-values for which the derivative is positive and negative.Now that we are looking at a calculus problem rather than an algebra problem, we need to learn some calculus. The first thing that we must do is to find the critical numbers for the derivative. A critical number is defined as a number c in the domain of f where $f'(c) = 0$ or $f'(c)$ does not exist. Once you have the derivative, you need to determine the values for which the derivative is zero or where it is undefined. For this example, the critical numbers are $x = 4$, $x = 0$, and $x = 6$. These are the x-values that we need to place on our number line to divide it into sections. Then we pick test values in each section of the number line to determine if the derivative is positive or negative on that interval.
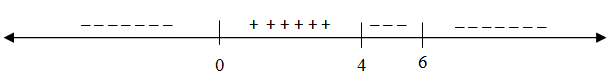
Choosing $x = -1$ as our test value in the first section of the number line, we can see that the numerator will be positive and the denominator will be negative so we can conclude that the derivative is negative on that interval.
Selecting $x = 1$ as our test value in the second section of the number line, we can see that the numerator will be positive and the denominator will be positive so we can conclude that the derivative is positive on that interval.
Picking $x = 5$ as our test value in the third section of the number line, we can see that the numerator will be negative and the denominator will be positive so we can conclude that the derivative is negative on that interval.
Selecting $x = 7$ as our test value in the final section of the number line, we can see that the numerator will be negative and the denominator will be positive so we can conclude that the derivative is negative on that interval.
Our solution is that $f'(x) > 0$ on $(0, 4)$ and $f'(x) < 0$ on $(-\infty, 0) \cup (4, 6) \cup (6, \infty)$. In calculus class, you will learn more about why we want this information.
Example 8.3:
Determine the x-values for which the derivative is positive and negative.We make a couple of observations:
- We were given the function, not the derivative.
- This function has a restricted domain, $[0, \infty)$.
First, this means that we need to take the derivative. Second, when we create our number line, it will not have arrows on both ends.
| $f(x)$ | $=$ | $\sqrt{x}e^{-x}$ | |
| $f'(x)$ | $=$ | $\sqrt{x}(-e^{-x}) + e^{-x}\left(\frac{1}{2}x^{-1/2}\right)$ | We must use the product rule for the derivative. |
| $=$ | $-x^{-1/2} \cdot e^{-x}\left(x - \frac{1}{2}\right)$ | We factor out the common factors of $-x^{-1/2}$ and $e^{-x}$. | |
| $=$ | $\dfrac{-\left(x \; - \; \frac{1}{2}\right)}{\sqrt{x} \; \cdot \; e^{x}}$ | Then we must rewrite the derivative with no negative exponents. |
Now that we have the derivative in simplified form, we can find the critical numbers. These are $x = 0$ and $x = \frac{1}{2}$. One observation that is worth making is that the $e^x$ portion of the derivative does not give us any critical numbers because $e^x$ is never 0; in fact, $e^x > 0$ for all x.

Choosing $x = \frac{1}{4}$ as our test value in the first section of the number line, we can see that the numerator will be positive and the denominator will be positive so we can conclude that the derivative is positive on that interval.
Picking $x = 1$ as our test value in the second section of the number line, we can see that the numerator will be negative and the denominator will be positive so we can conclude that the derivative is negative on that interval.
Our solution is that $f'(x) > 0$ on $\left(0, \frac{1}{2}\right)$ and $f'(x) < 0$ on $\left(\frac{1}{2}, \infty\right)$.
Example 8.4:
Determine the values of $\theta$ for which the derivative is positive and negative in the interval $[-2\pi, 2\pi]$.Again, we are given the function rather than the derivative and in this example, we are given the restricted interval. The derivative of the function is $f'(\theta) = 1 - \sin(\theta)$, which tells us that we will have a critical number when $\sin(\theta) = 1$, and this is true for two angles in the given interval $\theta = \frac{\pi}{2}$ and $\theta = \frac{-3\pi}{2}$. Since we were given a closed interval, those values are the endpoints of our number line.
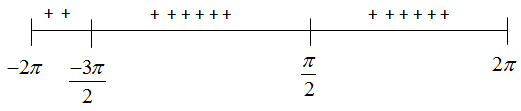
Choosing $\theta = \frac{-7\pi}{4}$ as our test value in the first section of the number line, we can conclude that the derivative is positive on that interval.
Selecting $\theta = 0$ as our test value in the second section of the number line, we can conclude that the derivative is positive on that interval.
Picking $\theta = \frac{3\pi}{4}$ as our test value in the last section of the number line, we can conclude that the derivative is positive on that interval.
Now looking at the derivative again and using our common sense, we can see that since $-1 \leq \sin(\theta) \leq 1$, then $f'(\theta) = 1 - \sin(\theta) \geq 0$ for all values of $\theta$.