Lab 3: Special Functions (Exponential, Logarithmic, and Trigonometric)

The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.

Trigonometric Functions

Trigonometry is important to the study of calculus. In addition to knowing the right triangle definitions of the six trigonometric functions, you should know the unit circle and some basic trig identities (see the Prerequisite Material reading section). In calculus, we always use radian measure instead of degree measure when referring to angles. Below are the graphs of the six basic trigonometric functions, along with their domains and ranges. As in the prerequisite material, the graphs with highlighted labels are ones that you should know.

Example 3.1

$f(x) = \sin(x)$

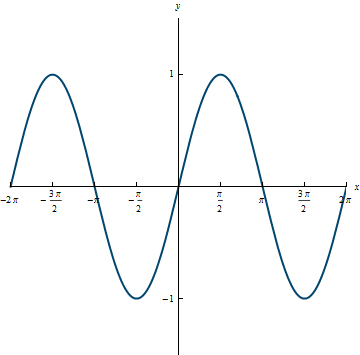
Domain: $(-\infty, \infty)$

Range: $[-1, 1] $

Example 3.2

$f(x) = \csc(x) = \frac{1}{\sin(x)}$

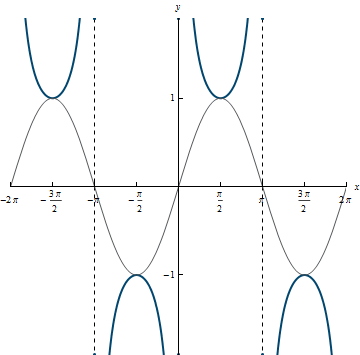
Domain: $\{x|x \ne k\pi, k \in \mathbb{Z}\}$

Range: $(-\infty, -1] \cup [1, \infty) $

Example 3.3

$f(x) = \cos(x)$

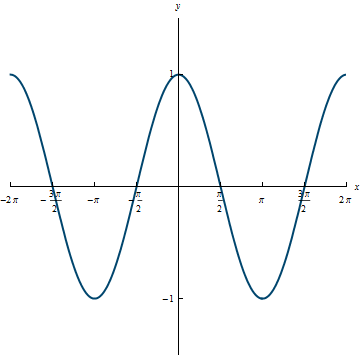
Domain: $(-\infty, \infty)$

Range: $[-1, 1] $

Example 3.4

$f(x) = \sec(x) = \frac{1}{\cos(x)}$

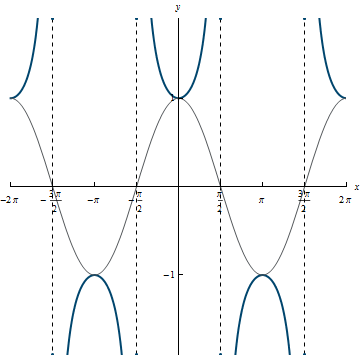
Domain: $\Big\{x|x \ne \frac{(2k \, + \, 1)\pi}{2}, k \in \mathbb{Z}\Big\}$

Range: $(-\infty, -1] \cup [1, \infty) $

Example 3.5

$f(x) = \tan(x)$

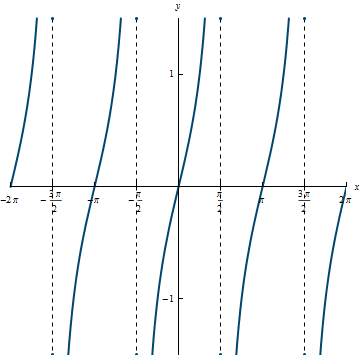
Domain: $\Big\{x|x \ne \frac{(2k \, + \, 1)\pi}{2}, k \in \mathbb{Z}\Big\}$

Range: $(-\infty, \infty) $

Example 3.6

$f(x) = \cot(x) = \frac{1}{\tan(x)}$

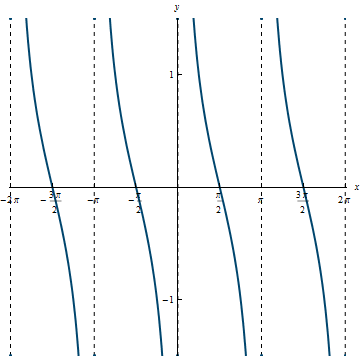
Domain: $\{x|x \ne k\pi, k \in \mathbb{Z}\}$

Range: $(-\infty, \infty) $

If you look back at the transformations of graphs in the prerequisite material and apply some of these transformations to the trigonometric functions, then you may see graphs such as the following examples.

Example 3.7

$y = \sin(2x)$

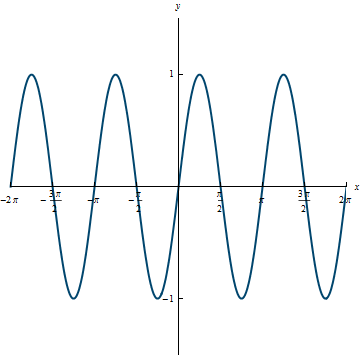
The number 2 in this equation changes the period of the sine curve so that it will repeat itself every $\pi$ units, instead of the standard $2\pi$ units.

Example 3.8

$y = \sin\!\left(\frac{1}{2}x\right)$

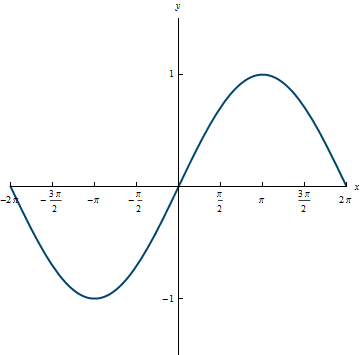
The fraction 1/2 in this equation changes the period of the sine curve so that it will repeat itself every $4\pi$ units instead of every $2\pi$ units.

If the coefficients are placed in front of the function instead of in front of the variable, the amplitude of the trigonometric function will change as seen in the following examples.

Example 3.9

$y = 2 \sin(x)$

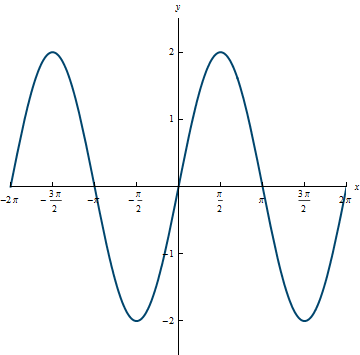
The number 2 in this equation changes the amplitude of the sine curve so that the range of this function is $[-2, 2]$ instead of $[-1, 1]$.

Example 3.10

$y = -3 \sin(x)$

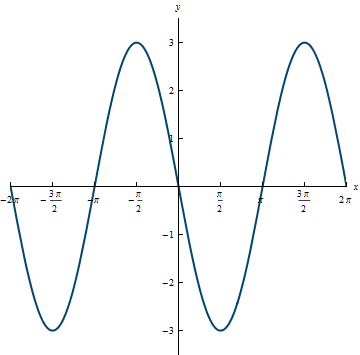
The number 3 in this equation changes the amplitude and the negative in front of the 3 reflects the graph across the x-axis.

Exponential Functions

An exponential function is a function of the form $f(x) = a^{x}$, where the base a is a positive constant not equal to 1. Some examples are given below. It is a good idea to review the laws of exponents (Basic Algebraic Operations lab) as these laws are useful when working with exponential functions.

Example 3.11

$f(x) = y = 2^x$

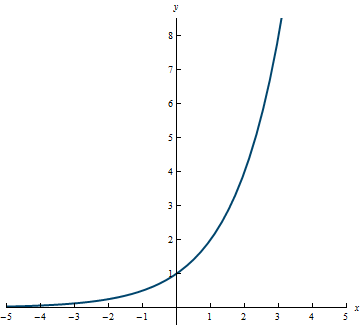
Domain: $(-\infty, \infty)$

Range: $(0, \infty)$

Example 3.12

$f(x) = y = \left(\frac{1}{2}\right)^x = 2^{-x}$

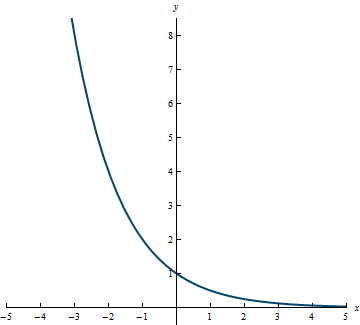
Domain: $(-\infty, \infty)$

Range: $(0, \infty)$

In calculus the most common exponential function that you will work with is $f(x) = e^x$. This exponential function is used in modeling population growth, radioactive decay, and Newton's Law of Cooling.

Example 3.13

$f(x) = y = e^x $

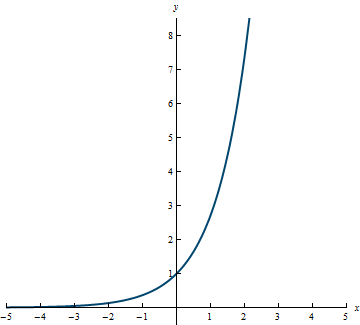
Domain: $(-\infty, \infty)$

Range: $(0, \infty)$

Example 3.14

$f(x) = y = e^{-x} $

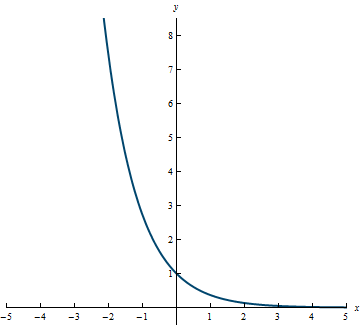
Domain: $(-\infty, \infty)$

Range: $(0, \infty)$

Inverse Functions

Before we introduce the next type of function, let’s review the concept of inverses. In order for a function to have an inverse that is also a function, the original function must be one-to-one.

One-to-one—A function f is called a one-to-one function if it never takes on the same value twice (i.e., for each output value (y-value) there is only one input value (x-value)).

One easy way to check to see if a function is one-to-one is to use the horizontal line test on the graph of the function.

Horizontal Line Test—A function is one-to-one if and only if any horizontal line intersects its graph at most once.
Inverse function—Given a one-to-one function f with domain D and range R, then its inverse function $f^{-1}$ has domain R and range D and is defined by $f^{-1}(y) = x \Leftrightarrow f(x) = y$ for any y in R.

Note:

$f^{-1}(x)$ is NOT the same as $\frac{1}{f(x)}$.

Example 3.15

$f(x) = x^2$

Not one-to-one, so its inverse is not a function.

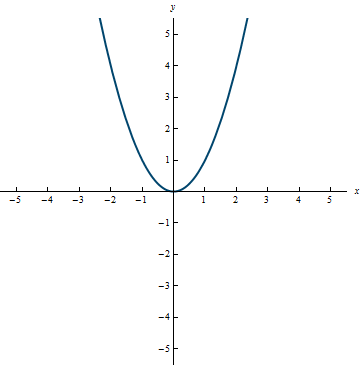
The graph of the inverse relation of $f(x) = x^2$ is shown here. Clearly, it is not a function because it doesn’t pass the vertical line test.

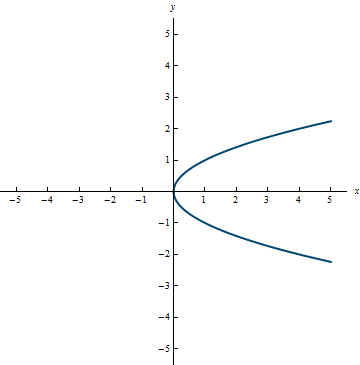
Example 3.16

$f(x) = x^3$

One-to-one, so its inverse is a function.

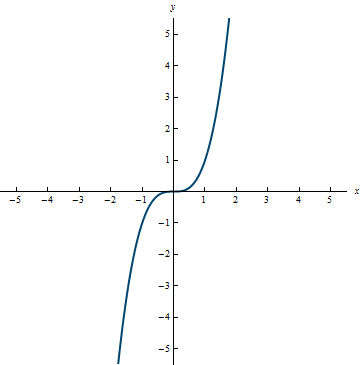
The graph of the inverse of $f(x) = x^3$ is shown here. Notice that it will pass the vertical line test so it is a function.

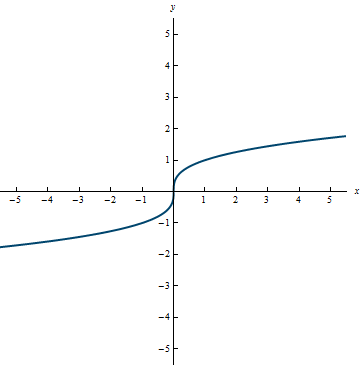
Notice that the function and the inverse function in Example 3.16 are familiar. The function $f(x) = x^3$ has an inverse of $f^{-1}(x) = \sqrt[3]{x}$.

One observation that you might make from the graphs in Example 3.16 is that it looks like the graph of $y = f^{-1}(x)$ can be obtained by flipping the graph of $y = f(x)$ across the line $y = x$. This is illustrated in the following examples.

Example 3.17:

Visual representation of $f(x) = x^3$ and its inverse $f^{-1}(x) = \sqrt[3]{x}$.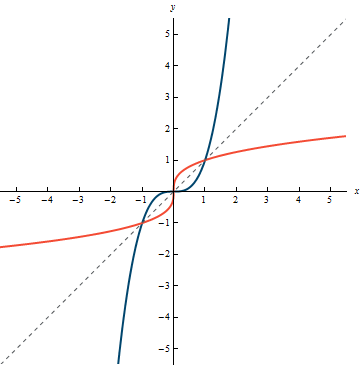

Example 3.18:

Visual representation of $f(x) = e^x$ and its inverse $f^{-1}(x) = \ln(x)$.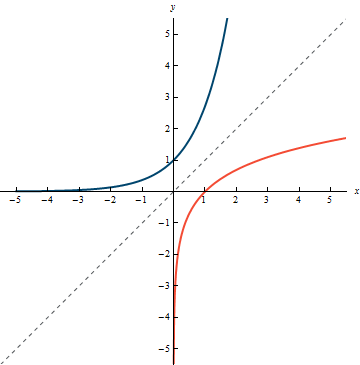

Compositions

Composition of f and g—Given two functions f and g, the composite function $f \circ g$ is defined by $(f \circ g)(x) = f(g(x))$.

When you compose a function and its inverse, you always get x for all x in the domain of the inside function. In other words, $(f^{-1} \circ f)(x) = x$ for all x in the domain of f. Likewise, $(f \circ f^{-1})(x) = x$ for all x in the domain of $f^{-1}$.

Example 3.19:

Determine whether or not the following functions are inverses of each other.

$f(x) = 3x - 5$ and $g(x) = \frac{1}{3}x + \frac{5}{3}$

One way to check to see if functions are inverses would be to graph both of these functions and see if they are reflections of each other in the line $y = x$. We will try to determine if they are inverses in two ways, both of which are algebraic.

Method 1: Find the inverse of one of the functions and see if that inverse is equal to the other function. Here, we will find the inverse of $f(x)$.

$f(x)$	$ = $	$ 3x - 5 $
$ y $	$= $	$ 3x - 5 $	We first replace f(x) with y.
$ x $	$= $	$3y - 5 $	Then we switch x and y around.
$ x + 5$	$ = $	$3y$	Now we solve the new equation for y in terms of x.
$ \frac{(x \, + \, 5)}{3}$	$ = $	$ y $	Now we solve the new equation for y in terms of x.

This gives us that $f^{-1}(x) = \frac{(x \, + \, 5)}{3} = \frac{1}{3}x + \frac{5}{3}$. Since this equals the function g(x) we were given, we have that f(x) and g(x) are inverses of each other.

Method 2: Compose the functions and see if the result of the composition is equal to x.

$(f \circ g)(x)$	$=$	$f(g(x))$
	$=$	$f\left(\frac{1}{3}x + \frac{5}{3}\right)$	We plug the function g(x) into f wherever there is an x.
	$=$	$3\left(\frac{1}{3}x + \frac{5}{3}\right) - 5$	We now simplify algebraically and the end result is x.
	$=$	$x + 5 - 5$	We now simplify algebraically and the end result is x.
	$=$	$x$
$(g \circ f)(x)$	$=$	$g(f(x))$
	$=$	$g(3x - 5)$
	$=$	$\frac{1}{3}(3x - 5) + \frac{5}{3}$
	$=$	$x - \frac{5}{3} + \frac{5}{3}$
	$=$	$x$

Since $(f \circ g)(x) = x$ and $(g \circ f)(x) = x$, we can determine that f(x) and g(x) are inverses of each other.

Composition of functions is also important in calculus because often we have to "decompose" a function into its parts. This idea is particularly important when performing the chain rule when taking derivatives of a function that is the composition of other functions. This idea of decomposing a function is illustrated in the next example.

Example 3.20:

Given $F(x) = \sqrt{\cos(x)}$ find f(x) and g(x) so that $F(x) = (f \circ g)(x)$.

Since we know that $(f \circ g)(x)$ is the same as $f(g(x))$, we know that g has to be the "inside" function so we let $g(x) = \cos(x)$, and since f has to be the "outside" function we let $f(x) = \sqrt{x}$. Now we need to check our answer, so using our selected f(x) and g(x), we need to make sure that we get the correct F(x).

$ \begin{array}{rcl} (f \circ g)(x) & = & f(g(x)) \\ & = & f(\cos(x)) \\ & = & \sqrt{\cos(x)} \\ & = & F(x) \end{array} $

Logarithmic Functions

For some functions, it is not possible to find an inverse using algebraic means, even though one exists. Therefore, we give the inverse function a name and define it in terms of the original function. For example, $f(x) = \log_a(x)$ is the inverse of the function $f(x) = a^x$. We say that $\log_a(x) = y$ when $a^y = x$.

A logarithmic function is a function of the form $f(x) = \log_a(x)$, where the base a is a positive constant not equal to 1. Logarithmic functions are inverses of exponential functions.

There are two types of logarithmic functions that are dealt with frequently. The common logarithm is defined as $f(x) = \log_{10}(x)$. On your calculator, the LOG key refers to the common logarithm. The natural logarithm is used more in calculus (and higher level mathematics). It is defined as $f(x) = \log_e(x) = \ln(x)$. On your calculator, the LN key refers to the natural logarithm.

The graph of $f(x) = \ln(x)$ is shown in Example 3.21. The graph should not be surprising since it is the inverse function of $y = e^x$.

Example 3.21

$f(x) = \ln(x)$

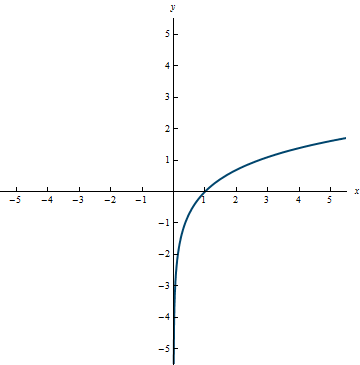
Domain: $(0, \infty)$

Range: $(−\infty, \infty)$

We know that Example 3.13 and Example 3.21 are inverses of each other. Some observations to notice are that the domain for Example 3.13 is the range for Example 3.21; and the range for Example 3.13 is the domain for Example 3.21. This is not a coincidence—it follows from the fact that they are inverses of each other.

Since we are talking about logarithmic functions, it might be a good time to review some properties of logarithms.

Properties of Logarithms—Given that a, x, and y are positive numbers, then the following are true.
1. $\log _{a}(xy) = \log_{a}(x) + \log_{a}(y)$
2. $\log_{a}\!\left(\frac{x}{y}\right) = \log_{a}(x) - \log_{a}(y) $
3. $\log_{a}(x^{r}) = r \log_{a}(x)$, where r is any real number and $x > 0$.
4. $\ln(e^{x}) = x$, $x \in \mathbb{R} $
5. $e^{\ln(x)} = x$, $x > 0$

Properties 4 and 5 follow directly from the fact that $f(x) = e^x$ and $f^{-1}(x) = \ln(x)$ are inverses of each other.