Lab 6: Review of Geometry and Algebra for Related Rate Problems
The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.
In first semester calculus you will encounter related rate problems, which require some special formulas and concepts from geometry, algebra, and trigonometry. In this lab, we will focus on reviewing some of these concepts. This will help you with setting up the equations that are needed to solve the related rate problems.
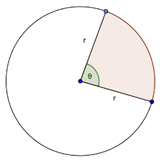
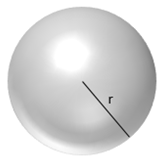
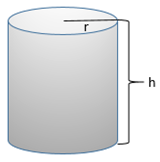
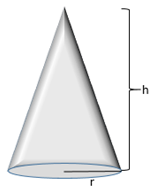
Some useful geometric formulas that you must know include the area of a sector of a circle, the volume and surface area of a sphere, the volume and surface area of a cylinder, and the volume of a cone. Note that the formula for the surface area of a cylinder depends on whether or not you include the top and bottom circles of the cylinder.
| Sector of a Circle | Sphere | Cylinder | Cone |
|---|---|---|---|
 |
 |
 |
 |
| A = \frac{1}{2}r^2\theta (\theta in radians) | V = \frac{4}{3}\pi r^3 A = 4\pi r^2 |
V = \pi r^2h A = 2\pi r^2 + 2\pi rh |
V = \frac{1}{3}\pi r^2h |
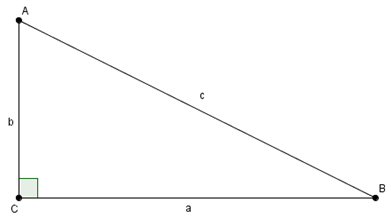
A couple other formulas that may appear in some of the word problems are the Pythagorean Theorem and the distance formula. You can see that the distance formula is really a special case of the Pythagorean Theorem.
| The Pythagorean Theorem | Distance Between Two Points P1 and P2 |
|---|---|
 |
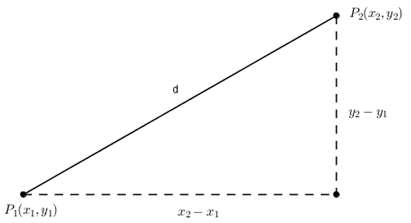 |
| a^2 + b^2 = c^2 | d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} |
It would also be a good idea to review some right triangle trigonometry, which can be found in Lab 0: Prerequisite Material. Another concept from geometry that is helpful in solving related rate problems is the concept of similar triangles.
- Definition of similar triangles—Two triangles are similar if corresponding angles are congruent and corresponding sides are proportional.
Looking at the triangles in Figure 6.1 below, we can see that the corresponding angles are congruent. To determine whether the corresponding sides are proportional, we need to look at each of the three ratios and determine whether the ratios are the same. If we look at the side opposite the 75° angle in the big triangle and the side opposite the 75° angle in the small triangle, we see that the ratio is \frac{10.8}{5.4} or \frac{2}{1}. If we do the same process for the other two sides, we see that the ratios are \frac{8.6}{4.3} or \frac{2}{1} and \frac{9.2}{4.6} or \frac{2}{1}. Since we get the same ratio every time, these two triangles are similar.
Figure 6.1
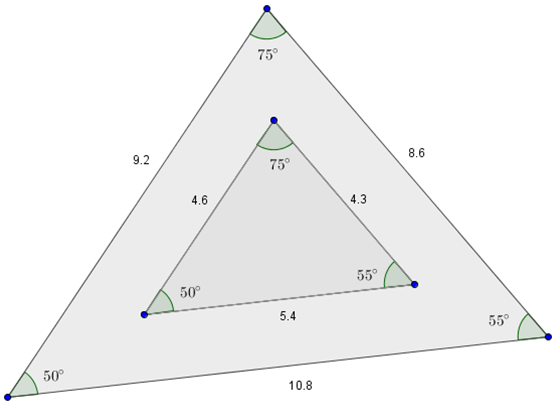
There are three theorems in geometry that help us prove that triangles are similar: AAA (Angle, Angle, Angle), SSS (Side, Side, Side), and SAS (Side, Angle, Side).
The following examples are types of related rate problems that you might encounter in calculus. While we are including the entire problem in the examples, we will only demonstrate the algebra and geometry behind setting up the problem so that it is ready to solve using calculus. We will not actually do the calculus part of the problem.
Example 6.1:
A ladder 10 meters long rests on horizontal ground and leans against a vertical wall. The foot of the ladder is pulled away from the wall at the rate of 0.5 m/sec. How fast is the top sliding down the wall when the foot of the ladder is 6 m from the wall?The first step in most of these types of problems is to draw a picture of the situation. Now looking at the picture, you notice that there is a right triangle. It is a good time to use the Pythagorean Theorem. This gives us the equation, x^2 + y^2 = 10^2. For lab, this is where we stop, but to finish the problem using calculus, you would first differentiate both sides of the equation implicitly with respect to time, t.
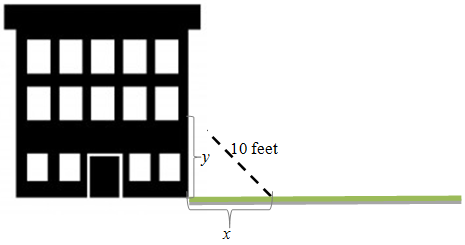
Example 6.2:
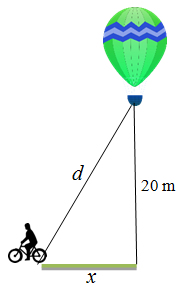
A balloon is at a height of 20 meters, and is rising at the constant rate of 5 m/sec. A bicyclist passes beneath it, traveling in a straight line at the constant speed of 10 m/sec. How fast is the distance between the bicyclist and the balloon increasing 2 seconds later?This problem is similar to the ladder problem in Example 6.1 as there is a right triangle involved with the problem. But in this picture the height of the balloon at the time of interest is fixed at 20 meters. So our equation is now x^2 + 20^2 = d^2.
Example 6.3:
A conical tank has height 3 m and radius 2 m at the top. Water flows in at a rate of 1.1 m3/min. How fast is the water level rising when it is 1.9 m from the bottom of the tank?Since we are given the rate at which the water flows into the tank, we realize that we need to use the volume of the cone. From our earlier information, we know that the volume of a cone is given by the formula, V = \frac{1}{3}\pi r^2h. By reading the problem, we know that we need to find out how fast the height (altitude) is changing at a specific moment. One thing to observe is that as the water level rises the radius of the circle found at the top of the water level will also change. So it appears that we have too many unknown variables in the related rate problem.
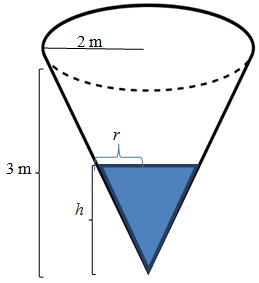
If you recall in the previous two examples, there were two unknowns in each one. Is there a way to eliminate one of the variables from the volume formula? If you read the problem carefully again, you notice that we are being asked to find how fast the water level is rising so we want to make sure that the variable h is left in our formula. Looking at the picture of the conical tank above, you notice that there appears to be similar figures. If we think of this picture in two dimensions instead of three, our picture would look like the one below.
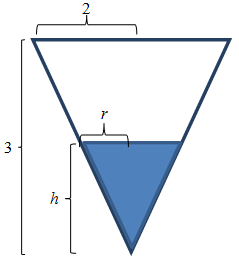
We have a pair of similar triangles so their side lengths are proportional. This gives us the following equation, \frac{h}{3} = \frac{r}{2}. Solving for r we have that r = \frac{2}{3}h. Now we substitute this equation into the volume formula and get v = \frac{1}{3}\pi \left(\frac{2}{3}h\right)^2h = \frac{4}{27}\pi h^3. Now we have the volume equation down to two variables. For lab, we will stop here and not solve the calculus problem.