Lab 5: Inverse Trigonometric Functions
The following material should be read prior to attending lab. You are responsible for preparing for lab so that you don't slow down your group.
Hopefully by now you are becoming more comfortable with trigonometry. Recall the graphs of the six trigonometric functions from Lab 3. We know that these functions are periodic (i.e., the graph repeats itself after a certain period of time). So, how can these trigonometric functions have inverse functions? We have a problem because we know that for a function to have an inverse function, the original function must be one-to-one and none of these graphs will pass the horizontal line test. So, in order to discuss inverse trigonometric functions, we must take the original six trigonometric functions and restrict their domains so that they are one-to-one; then we can talk about their inverse function.
Let's look at the sine curve first and how we should restrict the domain. As seen in the graph below, it seems that if we restrict the domain of the sine function to the interval \left[\frac{-\pi}{2}, \frac{\pi}{2}\right], then we can still get the entire range of the function, [-1, 1]. Thus, the sine function has an inverse function with this restricted domain. Also, we know that the domain and range of the inverse function correspond to the range and domain of the original function (again, information from Lab 3). The notation that we will use for the inverse function of f(x) = \sin(x) is f^{-1}(x) = \sin^{-1}(x) = \arcsin(x) = \text{asin}(x).
Figure 5.1
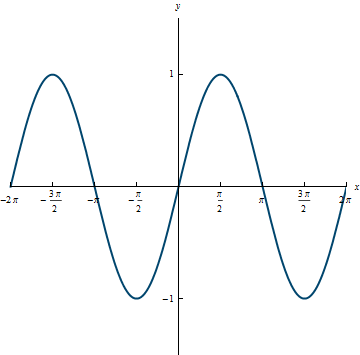
The graph is shown below in the darker color, with the graph of y = \sin(x) with restricted domain shown in the lighter color. Looking at these graphs, you can see that they are inverses of each other because the line y = x acts as a mirror for the two graphs.
Example 5.1
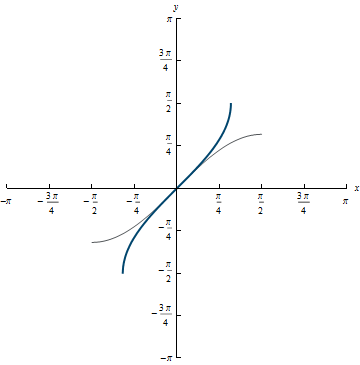
Domain: [-1, 1]
Range: \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]
This same process can be done for all six trigonometric functions so that they will be one-to-one and have inverse functions. The table below summarizes the six inverse trigonometric functions with their domain, range, and an illustration that may help you remember their range. The domain and range for arcsec(x) are not standard in all textbooks so you may have seen this differently somewhere else. Special thanks to my colleague and friend Sarah Clark for her suggestion on adding the illustration column to this table. It is helpful in remembering which quadrants form the range for each inverse function.
| Inverse Function | Domain | Range | Illustration of Range on the Unit Circle |
|---|---|---|---|
| \sin^{-1}(x) or \arcsin(x) | [-1, 1] | \left[- \frac{\pi}{2}, \frac{\pi}{2}\right] | 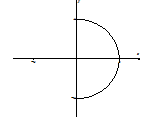 |
| \cos^{-1}(x) or \arccos(x) | [-1, 1] | [0, \pi] | 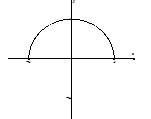 |
| \tan^{-1}(x) or \arctan(x) | (-\infty, \infty) | \left(- \frac{\pi}{2}, \frac{\pi}{2}\right) | 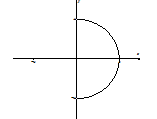 |
| \csc^{-1}(x) or \text{arccsc}(x) | (-\infty, -1] \cup [1, \infty) | \left(0, \frac{\pi}{2}\right] \cup \left(\pi, \frac{3\pi}{2}\right] | 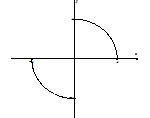 |
| \sec^{-1}(x) or \text{arcsec}(x) | (-\infty, -1] \cup [1, \infty) | \left[0, \frac{\pi}{2}\right) \cup \left[\pi, \frac{3\pi}{2}\right) | 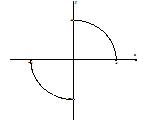 |
| \cot^{-1}(x) or \text{arccot}(x) | (-\infty, \infty) | (0, \pi) | 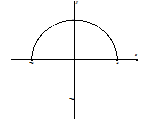 |
Let's look at two other important inverse trigonometric functions and their graphs. Both graphs contain the trigonometric function on a restricted domain so you can see that the two functions are inverses of each other.
Example 5.2
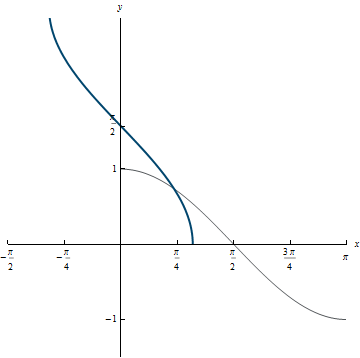
Domain: [-1, 1]
Range: [0, \pi]
Example 5.3
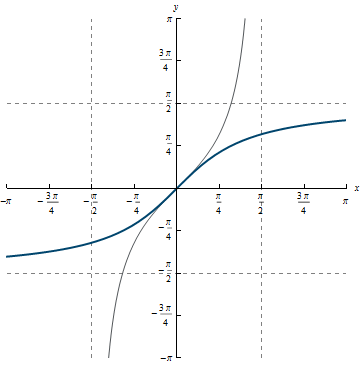
Domain: (-\infty, \infty)
Range: \left(- \frac{\pi}{2}, \frac{\pi}{2}\right)
Now let's work through a couple of problems involving inverse trigonometric functions so you feel more confident in your knowledge.
Example 5.4
Find the exact value of the expression \sin\!\left(\frac{\pi}{3}\right).This problem involves knowing your unit circle and is a review of information from Lab 0: Prerequisite Material. Essentially we need to find the y-coordinate of the point corresponding to the angle, \frac{\pi}{3}. So, our answer needs to be a number between −1 and 1 because that is the range of the sine function. Looking back at the unit circle in Lab 0, we see that the y-coordinate of the angle \frac{\pi}{3} is \frac{\sqrt{3}}{2}. This fact is something that you should NOT have to look up—you should know this answer without having to look at the unit circle. Since the sine of the angle corresponds to the y-coordinate of the point, we have \sin\!\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}.
In the next example, you are given information about the point on the unit circle and you need to find the angle that corresponds to this information. It is very important to pay attention to the range of the inverse trigonometric functions because it tells you which angles are allowed for your answers. The statement \sin^{-1}(x) = y that means that \sin(y) = x. For a trigonometric function, the input value is an angle and the output is a number, while for an inverse trigonometric function, the input is a number and the output is an angle.
Example 5.5:
Find the exact value of each expression.(a) \sin^{-1}\!\left(\frac{-1}{2}\right)
Let's reword this problem so we can understand what is being asked. It is asking you to find the angle on the unit circle that has a sine (or y-value) equal to −1/2. If you go back and look at your unit circle, you realize that there is more than one answer. This is where the range of the inverse sine function becomes very important. The angle that we give as an answer must lie in this range.
Now, you can see that there is only one answer in the range and it is \frac{-\pi}{6}. Therefore, \sin^{-1}\!\left(\frac{-1}{2}\right) = \frac{-\pi}{6}.
(b) \tan^{-1}(1)
This question is asking us to find the angle on the unit circle that has a tangent equal to 1. It might be easier for us to think about this in terms of sine and cosine. Recall that \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}, so the angle that we are looking for must be the angle \alpha where \frac{\sin(\alpha)}{\cos(\alpha)} = 1. This means that \sin(\alpha) = \cos(\alpha), and since we know from our unit circle that means the x- and y-coordinates of the point must be equal. You will notice that this occurs more than once, but remember that our answer has to lie in the range of the inverse tangent function. So, we can see that this happens when \alpha = \frac{\pi}{4}. Thus, we have that \tan^{-1}(1) = \frac{\pi}{4}.
In addition to these types of problems, you may also encounter other problems in calculus involving the inverse trigonometric functions. For example, you may be asked to find the exact value of \sin\!\left(\sin^{-1}\!\left(\frac{\sqrt{2}}{2}\right)\right). We need to follow the proper order of operations so we would look at the inside function first and determine that \sin^{-1}\!\left(\frac{\sqrt{2}}{2}\right) = \frac{\pi}{4}, so the problem then becomes \sin\!\left(\frac{\pi}{4}\right), which equals \frac{\sqrt{2}}{2}. This answer should not be surprising since the sine function and the inverse sine function are inverses of each other so the operations will "undo" each other and yield the quantity inside the parentheses. However, these types of problems are not always this easy, particularly when the inverse trig function is the outside quantity. Suppose we need to find the exact value of \sin^{-1}\!\left(\sin\!\left(\frac{7\pi}{6}\right)\right). Again, following the order of operations, we need to look at the inside quantity first and we discover that the angle is located in the 3rd quadrant and knowing our unit circle, we have that \sin\!\left(\frac{7\pi}{6}\right) = \frac{-1}{2}. Now replacing that in our original problem gives us that we want to find \sin^{-1}\!\left(\frac{-1}{2}\right) and using our knowledge gained in this section, we know that the desired angle is \frac{-\pi}{6}, which is in the 4th quadrant. Therefore, \sin^{-1}\!\left(\sin\!\left(\frac{7\pi}{6}\right)\right) = \frac{-\pi}{6}. The key to determining whether these problems are going to be fairly easy (as in the first example) or more difficult (as in the second example) is to look at which function is on the outside of the expression. If the inverse trig function is on the inside, then the problem will be much easier to solve.
As you are about to learn the derivatives for the inverse trig functions, it is important to discuss how these types of problems change when you are given an arbitrary angle, x. So, what does the expression \cos^{-1}(x) mean? We need to find the angle that has a cosine of x. This is easiest to understand if we think of a picture of a right triangle and use right triangle trigonometry. Let's label the angle in question, \alpha. Since \cos(\alpha) = x, then the picture can be labeled as in Figure 5.2. Then using the Pythagorean Theorem, we can determine the side opposite the angle \alpha as in Figure 5.3.
Figure 5.2
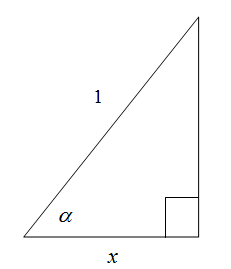
Figure 5.3
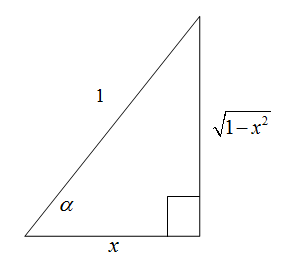
Using Figure 5.3, we can determine that \tan(\cos^{-1}(x)) = \frac{\sqrt{1 \, - \, x^2}}{x}.