Chapter 7 – States of Matter and Changes in State
Introduction
The materials we deal with every day exist in one of three states of matter: solid, liquid, or gas. The molecules in the liquid and solid phase are much closer to one another than are the molecules in the gas state. Consequently, the solid and liquid states are often called the condensed states. Some substances, such as water, are found in all three states under normal conditions (ice, water, and steam). However, most other substances are found in only one state under normal conditions. Thus, most of us have only encountered elemental iron as a solid, helium as a gas, and table salt as a solid. In this chapter, we examine the properties of the states of matter.7.1 Gases
Introduction
Gases are characterized by their volume (V), pressure (P), temperature (T), and the number of moles of particles (n). In this section, we discuss how the volume of a gas is affected by changes in its pressure, temperature, and number of moles. Finally, we consider mixtures of gases.Objectives
-
•Explain how a barometer is used to determine atmospheric pressure.
-
•Determine the pressure of a gas with a manometer reading and atmospheric pressure.
-
•Explain how the volume of a gas varies with its pressure (sketch V vs. P for an amount of gas at constant T).
-
•State Boyle's Law and use it to determine the volume of a gas at one pressure from its volume at a different pressure but at the same temperature.
-
•Explain how the volume of a gas varies with its temperature (sketch V vs. T for an amount of gas at constant pressure).
-
•Convert a temperature from the Celsius scale to the Kelvin scale and vice versa.
-
•State Charles's Law and use it to determine a volume of a gas at one temperature given its volume at a different temperature.
-
•State the Ideal Gas Law.
-
•Use the Ideal Gas Law.
-
•Define partial pressure.
-
•Determine the pressure of a mixture of gases from the partial pressures of the component gases.
-
•Define molarity and determine the molarity of a gas from its pressure and temperature or the number of moles of gas and its volume.
Boyle's Law and Pressure
7.1-1. Boyle's Law and Pressure
Barometric pressure is usually given by the height of a mercury column that the atmosphere will support.
-
•High: 809 mm = 31.9 in = 1.06 atm (Alaska, 1969)
-
•Low: 670 mm = 26.3 in = 0.88 atm (Florida, 1935)
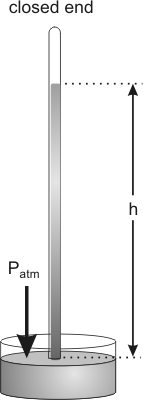
Figure 7.1: A Barometer
The pressure exerted by the weight of the mercury column of height h equals the pressure exerted by the weight of the atmosphere.
7.1-2. Measuring Pressure with a Manometer
The pressure of a gas in the laboratory is often found as the difference in heights of two columns of a liquid (most often mercury) in a manometer.
-
•Pgas = Patm + h if mercury level is higher on atmosphere side
-
•Pgas = Patm – h if mercury level is higher on gas side
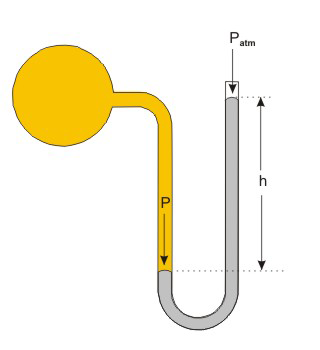
Figure 7.2: Determining Pressure with a Manometer
A manometer, which is used to measure the pressure of a gas: In the above experiment, the pressure of the gas (P) is greater than barometric pressure (Patm) by h mm of Hg, i.e.,
P = Patm + h.
P = Patm + h.
7.1-3. Barometer Exercise
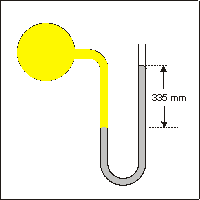
Exercise 7.1:
What is the pressure of the yellow gas in torr (mm Hg) if barometric pressure is 762 torr?
1097_0__
The pressure of the gas is greater than barometric pressure by 335 mm Hg because the column is higher on the atmosphere side. Thus, the pressure of the gas is P = Pbar + h = 762 + 335 = 1097 mm Hg or 1097 torr.
torr

What is the pressure of the yellow gas in atmospheres?
1.44_.04__
1 atm = 760 torr, so the pressure in atm is 1097 torr (1 atm/760 torr) = 1.44 atm.
atm

7.1-4. Boyle's Law
PV = k, where k is a constant that depends only upon the amount and temperature of the gas.
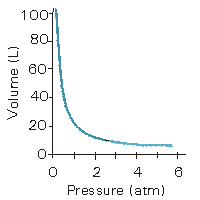
Figure 7.3: Volume of Gas vs. Pressure of Gas
The volume of one mole of a gas at 0 °C vs. the pressure of the gas is shown.
7.1-5 Boyle's Law Exercise
Exercise 7.2:
The pressure on 5.2 L of a gas is decreased from 1.0 to 0.75 atm at constant temperature. What is the new volume?
initial volume in liters
5.2___
The initial volume is the given volume, which is 5.2 L in this problem.
L

initial pressure in atmospheres
1___
The question indicates that the gas started at 1 atm, which is the initial pressure.
atm

final pressure in atmospheres
0.75___
The question indicates that the final pressure is 0.75 atm.
atm

final volume in liters
6.9___
The final volume is determined from the following: 
Vf = Vi ×
= (5.2 L) ×
= 6.9 L.
Note that the final volume equals the initial volume times a pressure change correction factor, which is a ratio of the pressures. Problems like this can be done with common sense rather than algebra if we recognize that pressure and volume must move in opposite directions. In this example, the pressure decreased, so we reason that the volume must increase, which means that the larger pressure must be in the numerator of the factor.
L
| Pf |
| Pi |
| 1.0 atm |
| 0.75 atm |
Temperature and Charles's Law
7.1-6. Charles's Law
V = kT, where k is a constant that depends on the amount and pressure of the gas, and T is the temperature in kelvins.
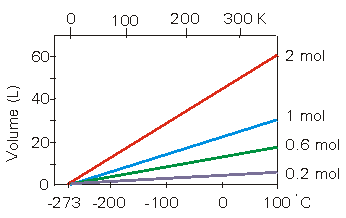
Figure 7.4: Charles's Law
The volume of the specified number of moles of gas as a funtion of temperature: The bottom scale is in degrees Celsius, and the top scale is the Kelvin scale.
7.1-7. Charles's Law Exercise
Exercise 7.3:
What is the volume of gas at 0 °C if the volume is 250 mL at 100 °C?
initial volume in milliliters
250_0__
The initial volume is the given volume, which is 250 mL in this problem. Note that the units of the answer will be the same as the units of the given volume, so it does not matter what those units are.
mL

initial temperature in kelvins
373___
The question indicates that the gas started at 100 °C, which must be converted to kelvins: K = 100 + 273 = 373 K.
K

final temperature in kelvins
273___
The question indicates that the gas started at 0 °C, which must be converted to kelvins: K = 0 + 273 = 273 K.
K

final volume in milliliters
182.98___
The final volume is determined from the following: 
Vf = Vi ×
= (250 mL) ×
= 183 mL.
Note that the final volume equals the initial volume times a temperature change correction factor, which is a ratio of the temperatures in kelvins. Problems like this can be done with common sense rather than algebra if we recognize that temperature and volume must move in the same direction. In this example, the temperature decreased, so we reason that the volume must also decrease, which means that the smaller temperature must be in the numerator of the factor.
mL
| Tf |
| Ti |
| 273 K |
| 373 K |
The Ideal Gas Law
7.1-8. Ideal Gas Law
PV = nRT is the ideal gas law.
| P | V | = | n | R | T |
| Pressure expressed in atmospheres: It can be expressed in other units, but that would change the value of R. | Volume of the gas expressed in liters: It can be expressed in other units, but that would change the value of R. | Number of moles of gas | R = 0.0821 L · atm · K–1 · mol–1: It is the gas law constant. | T is the absolute temperature in kelvins. |
Table 7.1
7.1-9. Ideal Gas Law Exercise
Exercise 7.4:
The ideal gas law can be used to solve for any one of the variables (P, V, n, or T) if the others are known. Things to remember when using R = 0.0821 L · atm · K–1 · mol–1:
-
•T is in kelvins.
-
•P is in atmospheres.
-
•V is in liters.
n =
0.45___
n = the number of moles, which is equal to the mass of He divided by the molar mass of He: 
1.8 g He ×
= 0.45 mol He.
mol
| 1 mol He |
| 4.0 g He |
R =
0.0821___
R = 0.0821 only when T is in K, P is in atm, and V is in L.
L · atm · K–1 · mol–1

T =
603___
Degrees Celsius must be converted to kelvins: T = 330 °C + 273.15 = 603.15 K.
K

V =
0.28_0__
V must be in liters: 
280 mL ×
= 0.28 L.
L
| 1 L |
| 1000 mL |
P =
79.66___
Solve PV = nRT for the pressure:
= 80 atm.
atm

| (0.45 mol)(0.0821 L · atm · K−1 · mol−1)(603 K) |
| 0.28 L |
Mixtures of Gases
7.1-10. Molarity
The molar concentration, or molarity, of a gas is the number of moles of gas present in 1 L.
7.1-11. Molarity Exercise
Exercise 7.5:
What is the concentration of fluorine (F2) in a 4.0-L flask that contains 4.2 g of fluorine?
1. Determine the number of moles of F2 (Mm = 38.00 g/mol).
n =
0.11___
The number of moles of F2 in the container is 
n = 4.2 g F2 ×
= 0.11 mol F2.
mol F2
| 1 mol F2 |
| 38.0 g F2 |
2. Calculate the molarity.

[F2]
=
0.028___
The concentration of fluorine in moles per liter (the molarity) is [F2] =
= 0.028 mol · L−1 = 0.028 M.
The fluorine concentration is 0.028 M (0.028 molar).
M
| 0.11 mol F2 |
| 4.0 L |
7.1-12. Partial Pressures
The pressure of a mixture of gases equals the sum of the partial pressures of the component gases.
PA =
to evaluate PA and PB, we obtain the following.
The total pressure of a mixture of gases equals the total number of moles of gas times RT/V.
| nART |
| V |
7.1-13. Partial Pressure Exercise
Exercise 7.6:
What are the partial pressures of Ne and He in a 6.0-L flask that contains 0.12 mol Ne and
0.19 mol He at 55 °C?
0.19 mol He at 55 °C?
PNe =
0.54___
The volume of each gas is V = 6.0 L, and the temperature of each gas is T = 273 + 55 = 328 K. Apply the Ideal Gas Law to each to obtain the following: 
PNe =
=
= 0.54 atm.
atm
| nNeRT |
| V |
| (0.12 mol)(0.0821 L · atm · K−1 · mol−1)(328 K) |
| 6.0 L |
PHe =
0.85___
The volume of each gas is V = 6.0 L, and the temperature of each gas is T = 273 + 55 = 328 K. Apply the Ideal Gas Law to each to obtain the following: 
PHe =
=
= 0.85 atm.
atm
| nHeRT |
| V |
| (0.19 mol)(0.0821 L · atm · K−1 · mol−1)(328 K) |
| 6.0 L |
What is the total pressure in the flask?
1.39___
The total pressure is the sum of the partial pressures: Ptot = 0.54 atm + 0.85 atm = 1.39 atm. Alternatively, the total pressure can be obtained from the Ideal Gas Law by using the total number of moles of gas, ntot = nNe + nHe = 0.12 mol + 0.19 mol = 0.31 mol: 
Ptot =
=
= 1.4 atm.
atm
| ntotRT |
| V |
| (0.31 mol)(0.0821 L · atm · K−1 · mol−1)(328 K) |
| 6.0 L |
7.1-14. Gas Law Exercise
Exercise 7.7:
A mixture contains 15 g Ne (AW = 20) and 10 g Ar (AW = 40) in a 5.0-L container at 30 °C.
Neon:
number of moles
0.75___
(15.0 g)(1 mol/20.0 g) = 0.75 mol Ne
mol Ne

molar concentration
0.15___
0.75 mol/5.0 L = 0.15 M Ne
M Ne

partial pressure in atm
3.7___
P = nRT/V = (0.75 mol)(0.0821 L · atm/K · mol)(303 K)/5.0 L = 3.7 atm Ne
atm Ne

Argon:
number of moles
0.25___
(10 g)(1 mol/40 g) = 0.25 mol Ar
mol Ar

molar concentration
0.050___
0.25 mol/5.0 L = 0.050 M Ar
M Ar

partial pressure in atm
1.244_0.044__
P = nRT/V = (0.25 mol)(0.0821 L · atm/K · mol)(303 K)/5.0 L = 1.2 atm Ar
atm Ar

What is the total pressure in the container?
4.9___
P = PNe + PAr = 3.7 + 1.2 = 4.9 atm
atm

7.2 Kinetic-Molecular Theory and Thermal Energy
Introduction
The ideal gas law applies only to gases that exhibit ideal gas behavior, which can deviate from real gas behavior. In this section, we examine the properties of ideal gases.Objectives
-
•Explain the meaning of temperature at the molecular level.
-
•Explain the meaning of thermal energy and determine the relative thermal energies of several gases.
7.2-1. Postulates
The behavior of gases is explained by kinetic-molecular theory, which is based on the four postulates provided below. Gases that obey all four postulates are called ideal gases.-
1The volume of the particles is negligible compared to the volume of the container. On average, the distances between gas particles are large compared to the size of the particles.
-
2The particles are in constant, random motion. Collisions are elastic, i.e., no kinetic energy is converted into potential energy.
-
3Particles in the gas phase do not interact with one another, i.e., there are no attractive forces between the particles, which is why the collisions are elastic (Postulate 2).
-
4The average kinetic energy of the molecules in a gas depends only on the absolute temperature of the gas. The kinetic energy of a particle isso hot molecules move faster than cold ones. This postulate provides the molecular definition of the absolute temperature:
mv2,1 2 -
•The absolute temperature of a system is a measure of the average kinetic energy of the molecules in the system.
-
7.2-2. Thermal Energy
Thermal energy, which is approximated as RT, is a measure of the average kinetic energy of the molecules.
-
•R = 8.31451 J · mol–1 · K–1 or
-
•R = 0.00831451 kJ · mol–1 · K–1
7.2-3. Thermal Energy Exercise
Exercise 7.8:
What is thermal energy at room temperature (25 °C)?
2.479___
First, convert temperature to kelvins: T = 273 + 25 = 298. Then, 
Ethermal ~ RT = (0.008314 kJ · mol−1 · K−1)(298 K) = 2.5 kJ · mol−1.
kJ/mol
What is thermal energy at 100 °C?
3.103___
T = 273 + 100 = 373, so 
Ethermal ~ RT = (0.008314 kJ · mol−1 · K−1)(373 K) = 3.1 kJ · mol−1.
kJ/mol
What is the approximate temperature at which Ethermal ~ 100 kJ/mol?
12027___
E ~ RT, so 
T ~
=
= 1.2 × 104 K.
K
| E |
| R |
| 100 × 103 J |
| 8.31 |
7.3 Intermolecular Interactions
Introduction
Why are some molecules gases, while others are liquids and solids at room conditions? Why does water expand upon freezing? The answers to both questions lie in the nature of the interaction between molecules, the topic of this section.Prerequisites
-
•1.7 Energy (Distinguish between kinetic and potential energy.)
-
•1.8 Electromagnetism and Coulomb's Law (Explain how the force of attraction of two opposite charges varies with their charge and the distance between them.)
-
•5.2 Bond Polarity (Represent the bond dipole with an arrow.)
-
•5.6 Determining Lewis Structures
Objectives
-
•Distinguish between intermolecular and intramolecular forces.
-
•Explain a temporary dipole and how it leads to dispersion forces.
-
•Describe a molecular dipole and represent it with an arrow.
-
•Use bond dipoles in a molecule to determine if there is a molecular dipole.
-
•Describe the hydrogen bond and state the requirements for it.
-
•Describe the structure of ice, explain why it has the structure it does, and use the structure to explain some physical properties of water.
7.3-1. Intermolecular Forces
Particles in the gas phase are relatively far apart, so their attractive forces are negligible compared to their thermal energy. However, the attractive forces between particles in the condensed states are strong enough to hold the particles in contact with one another. Ionic compounds are always solids at room temperature because their cations and anions are held in the solid network by strong electrostatic attractions called ionic bonds. However, molecular substances can occur as gases (O2), liquids (H2O), or solids (sugar) at room conditions. This diversity in states arises from a diversity in the strengths of the forces between the molecules. Whereas the strength of ionic bonds determines the physical properties of a salt crystal, the physical properties of molecular substances are not related to the strength of their covalent bonds. In molecular substances, we must distinguish between two different kinds of forces:-
1Intramolecular forces exist within a molecule. They are the bonds between atoms that hold the atoms together in the molecule.
-
2Intermolecular forces exist between molecules. They are the forces between different molecules that keep the molecules in the liquid and solid states.
Dispersion Forces
7.3-2. Dispersion Forces
Dispersion forces, which result from the interaction of induced dipoles, increase with molar mass.

Figure 7.5a: The Dispersion Force
Three molecules with no regions of charge have no way to interact.
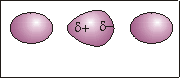
Figure 7.5b: The Dispersion Force
Random electron movement in the central molecule causes more electrons to be on one side and fewer on the other, which results in two charged regions.
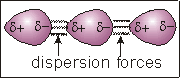
Figure 7.5c: The Dispersion Force
The charged regions on the central molecule induce charged regions on the adjacent molecules. The result is that the adjacent molecules have induced dipoles. The interaction of the opposite charges of the induced dipoles is called a dispersion force.
Molecular Dipoles
7.3-3. Dipolar Interactions
Dipolar forces act in addition to dispersion forces to increase the strength of the intermolecular interaction.
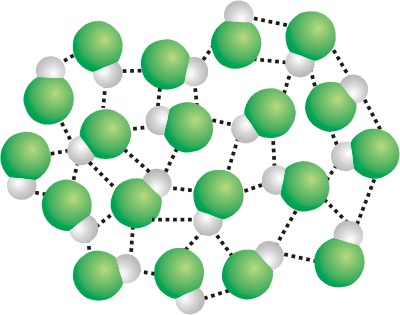
Figure 7.6: Dipolar interactions in HCl
Dipolar interactions (dotted lines) are between the chlorine atom (negative end of dipole) of one molecule and the hydrogen atom (positive end of dipole) on an adjacent molecule.
7.3-4. Charge Distribution
Molecules with a permanent asymmetric charge distribution are said to be polar or to have a molecular dipole.
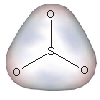
Figure 7.7a: Charge Distribution in SO3
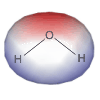
Figure 7.7b: Charge Distribution in H2O
7.3-5. Representing Molecular Dipoles
A molecular dipole is represented by an arrow that points from the positive pole toward the negative pole. A line is drawn through the arrow at the positive end to make "+" sign.
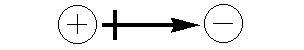
Figure 7.8
A molecule's permanent dipole is indicated by an arrow pointing from the center of positive charge toward the center of negative charge. A short line crosses the arrow forming a "+" at the positive end.
7.3-6. Effect of Geometry on Molecular Polarity
Molecular dipoles also depend upon molecular shape.
-
•Charge: The charge depends upon the electronegativity differences (strengths of the bond dipoles).
-
•Structure: The separation between dipoles depends upon the structure of the molecule. If the structure is such that the centers of negative and positive charge coincide, i.e., the separation is zero, the molecule is not polar.
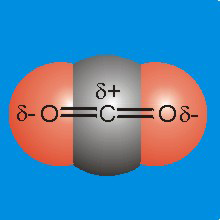
Figure 7.9a: Charge Distribution in CO2
-
•Charge: Oxygen (χ = 3.5) is more electronegative than carbon (χ = 2.5), so the oxygen atoms will carry some negative charge, while the carbon carries some positive charge.
-
•Structure: CO2 is linear, so the centers of positive and negative charge both reside on the carbon atom.
-
•Polarity: Since the centers of charge coincide, CO2 is not polar.
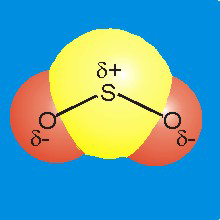
Figure 7.9b: Charge Distribution in SO2
-
•Charge: The electronegativity of sulfur is identical to that of carbon, so the charges carried by S and O in SO2 are identical to those carried by C and O in CO2.
-
•Structure: There is a lone pair on the sulfur atom, so sulfur dioxide is bent with an O–S–O bond angle of about 120°.
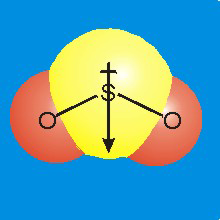
Figure 7.9c: Polarity in SO2
-
•Polarity: The center of positive charge is on the sulfur atom, but the center of negative charge lies at the midpoint of the line connecting the two oxygen atoms. Thus, the centers of positive and negative charge do not coincide, so SO2 is a polar molecule. The dipole points from the positive sulfur toward the center of negative charge between the two oxygen atoms.
7.3-7. Molecular Dipole of H2O
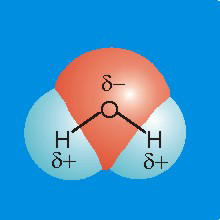
Figure 7.10a
-
•Charge: Oxygen is more electronegative than hydrogen, so it carries a partial negative charge, and the hydrogen atoms each carry a partial positive charge.
-
•Structure: There are two lone pairs on the oxygen atom, so water is bent with an H–O–H bond angle of about 109° (actually it is 104° due to a strong lp-lp interaction).
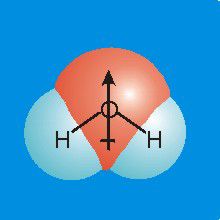
Figure 7.10b
-
•Polarity: The center of negative charge resides on the oxygen, while the center of positive charge resides on the line between the two hydrogen atoms. The two centers do not coincide, so water is a polar molecule (it contains a dipole). In fact, water is a very polar molecule. Its strong dipole plays an important role in its ability to dissolve ionic substances such as table salt.
7.3-8. Molecular Dipoles from Bond Dipoles
Molecular dipoles are the vector sum of the bond dipoles in a molecule.
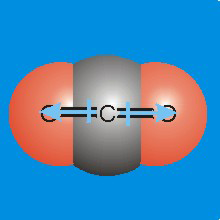
Figure 7.11a: Molecular dipoles are the sums of bond dipoles.
The bond dipole of each CO bond points from the carbon toward the oxygen. Because they point in opposite directions, they cancel one another, and CO2 does not have a molecular dipole, i.e., it is a nonpolar molecule.

Figure 7.11b: Molecular dipoles are the sums of bond dipoles.
Each SO bond has a bond dipole pointing from the sulfur toward the more electronegative oxygen. The sum of the two bond dipoles results in the molecular dipole represented by the red arrow.
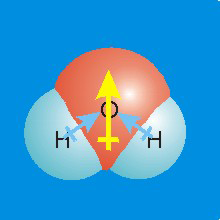
Figure 7.11c: Molecular dipoles are the sums of bond dipoles.
The OH bond dipoles (blue arrows) are at 104° angles. The resultant molecular dipole (yellow arrow) points from the center of the line connecting the hydrogens toward the oxygen.
7.3-9. Predicting Dipoles Exercise
Exercise 7.9:







Predict whether each of the following molecules is polar or nonpolar.
-
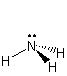
polar Each bond dipole points from a hydrogen to the more electronegative nitrogen, so the molecular dipole points from the center of the three hydrogen atoms toward the nitrogen.
-
nonpolar

-
polar
-
nonpolar CS2 is linear, so the bond dipoles, which point from the carbon to a sulfur, cancel. Consequently, CS2 is not polar.


-
polar HCN is linear, but the bond dipoles do not cancel because a C≡N bond is more polar than a C–H bond. Consequently, HCN is a polar molecule.
-
nonpolar


-
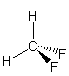
polar The bond dipoles do not cancel because the C–F bond is much more polar than the C–H bond. The molecular dipole points from the center of the hydrogen atoms toward the center of the fluorine atoms.
-
nonpolar

-
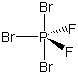
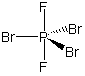
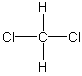
polar This is a commonly missed problem because the drawing is misleading. There are four electron groups around the carbon, so it is tetrahedral. None of the atoms in a tetrahedral structure are "opposite" one another as shown in the planar representation. See the preceding example for a better representation. As in the preceding example, the molecular dipole points from the center of the hydrogen atoms toward the center of the halogen atoms.
-
nonpolar

-
polar
-
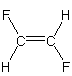
nonpolar We can neglect the C–H bonds as they are not polar. The bond dipoles of the two C–F bonds cancel, so the molecule is not polar.

-
polar We can neglect the C–H bonds as they are not polar. The bond dipoles of the two C–F bonds do not cancel, so the molecule is polar.
-
nonpolar

Hydrogen Bonding
7.3-10. Hydrogen Bonding
Hydrogen bonding is a strong dipolar force that can occur between a hydrogen atom and either a nitrogen, oxygen, or fluorine atom.
-
•Small size allows the interacting poles to get closer.
-
•Large electronegativity differences produce more charge on the poles.
-
•H–F bond: HF is the only molecule that contains an H–F bond.
-
•H–O bond: Water is a strong H-bonder, but there are many other molecules with O–H bonds.
-
•H–N bond: Ammonia is a strong hydrogen bonder, but there are many other compounds with H–N bonds.
7.3-11. H-bonding in Water
An oxygen atom in water can hydrogen bond to two hydrogen atoms on different water molecules.
Figure 7.12
7.3-12. Ice
In order to maximize the hydrogen bonding interactions, water molecules in ice orient relative to one another so that the two lone pairs on an oxygen interact with hydrogen atoms of two different water molecules. As a result, water crystallizes in a structure containing hexagonal channels (see Figure 7.13). These channels, which are created when water freezes, result in void space. The presence of the large amount of void space makes the solid less dense than the liquid. The following properties of ice are due to these channels.-
•Ice floats because the solid is less dense than the liquid.
-
•Pipes and radiators burst when water freezes in them because the water expands to create the channels.
-
•Ice crystallizes around the six-sided channels, so snowflakes are six-sided.
-
•Ice melts when pressure is applied because the pressure collapses the channels. One theory holds that ice skating is possible because the high pressure exerted by the skates melts the ice under them. The layer of liquid on top of the ice is what is actually slippery.
Figure 7.13: Structure of Ice
Predicting Relative Forces
7.3-13. Summary
As shown in Table 7.2, the relative strengths of the various interactions we have discussed overlap, so it is difficult to predict whether the interactions in a large nonpolar molecule are stronger or weaker than in a small polar molecule that hydrogen bonds. For example, I2 is a solid at room condition, while H2O is a liquid. Remember that dispersion forces are always present, so the interactions in a large polar molecule are probably stronger than in a small one. In the examples in Exercise 7.10, you will be asked to select the molecule in each pair that is expected to have the stronger interactions and the force responsible for the difference. Only one is responsible for the difference because the molecules have been chosen so that the other forces are comparable, not because they do not exist.| Type of Interaction | Energy of Interaction (kJ/mol) |
| Covalent Bond | 100–1000 |
| Hydrogen Bond | 10–50 |
| Dipolar Force | 5–25 |
| Dispersion | 1–50 |
Table 7.2: Relative Strengths of Interaction
7.3-14. Predicting Relative Strengths of Interaction Exercise
Exercise 7.10:








Predict the compound with the stronger interaction in each pair. Then indicate the force that is most responsible for the difference.
-
Compound:
-
CH3–O–CH3 No. The melting point of C2H5–O–H is much higher. The two compounds have the same formula but have very different melting points. Examine them carefully to determine the structural difference that would make their melting points so different.
-
C2H5–O–H Correct. The melting point of C2H5–O–H is much higher. The two compounds have the same formula but have very different melting points. Next, identify the force responsible for the difference.

-
Compound:
-
CH3–O–CH3 No. The compounds have similar structures, but different formulas. Use this fact to identify which of the three types of intermolecular forces is responsible for the difference.
-
C6H13–O–C6H13 Correct. The compounds have similar structures, but different formulas. Use this fact to identify which of the three types of intermolecular forces is responsible for the difference.

-
Compound:
-
NH4Cl Correct. PCl5 is a liquid at room conditions, while NH4Cl is a solid. Why?
-
PCl5 No. PCl5 is a liquid at room conditions, while NH4Cl is a solid. What is the difference between them?

-
Compound:
-
PH3 NH3 is a higher melting substance even though the compounds have similar structures and NH3 has a lower molar mass.
-
NH3 Correct. Now identify the force responsible.

-
Force:
-
dispersion The compounds have the same formula C2H6O, so they are expected to have very similar dispersion forces.
-
dipole-dipole C2H5–O–H is the more polar molecule, but dipole-dipole interactions are not the forces that are most responsible for the difference.
-
H-bonding The main difference between the intermolecular interactions of the two compounds is the H-bond. Remember that the requirement for a good H-bond is that H must be attached to an F, an O, or an N. The presence of an O–H bond in C2H5–O–H means that H-bonding is important in this molecule.
-
ionic bonding Neither compound is ionic.

-
Force:
-
dispersion Neither compound is very polar, and neither displays H-bonding, so the main difference between the two is their size. C6H13–O–C6H13 is the larger molecule, so it has the greater dispersion forces.
-
dipole-dipole Neither compound is very polar.
-
H-bonding There are no N–H, O–H, or F–H bonds.
-
ionic bonding Neither compound is ionic.

-
Force:
-
dispersion Dispersion forces are the most important forces in PCl5, but not in NH4Cl.
-
dipole-dipole The 5 P-Cl bond dipoles cancel, soPCl5 is not polar. NH4Cl is not a molecule so it cannot have dipole-dipole interactions.
-
H-bonding Although NH4Cl does have N–H bonds, it cannot display H-bonding because the nitrogen already has four electron regions.
-
ionic bonding Ammonium chloride is an ionic compound (NH41+ + Cl1–). As a general rule, ionic compounds are higher melting than molecular compounds because ionic bonds must be broken to melt ionic substances.

-
Force:
-
dispersion Dispersion forces are the most important forces in PCl5, but not in NH4Cl.
-
dipole-dipole Both compounds are polar, and ammonia is slightly more polar, but dipole-dipole interactions are not the main reason for the difference.
-
H-bonding Ammonia has N–H bonds, so it displays H-bonding.
-
ionic bonding Neither is ionic.

7.4 Solids
Introduction
Molecules in the solid and liquid states are much closer to one another than they are in the gas phase, so the solid and liquid states are referred to as the condensed states. Since the molecules are much closer, they interact much more strongly, and the strengths of those interactions dictate the properties of the substance.7.4-1. Introduction to Solids
The energy of interaction between particles in the solid state is much greater than thermal energy, so the particles in a solid sit in fixed positions relative to one another that maximize their interactions. Figure 7.14 shows the structure of NaCl, which has ions in each position. Each ion interacts with six ions of opposite charge, and the arrangement that is shown is the one that maximizes those interactions. Each particle has a fixed position, so solids have their own shape and volume, which are independent of the container. The kinetic (thermal) energy of each particle is in the form of oscillations about these positions. Thus, solids are characterized by an ordered array of particles, and that order allows us to understand their structures and properties. The structure/property relationships of solids are discussed in much more detail in the next chapter.
Figure 7.14
7.5 Liquids
Introduction
The intermolecular interactions in the liquid state are comparable to thermal energy, so the molecules remain relatively close to one another while undergoing random, but restricted, motion. This combination of hindered motion without fixed positions makes understanding liquids much more difficult than gases or solids. Liquids adopt the shape of the bottom of the container but maintain their own volume, which depends only slightly on the temperature. In this section, we introduce a few properties of liquids and relate them to the strengths of the intermolecular interactions.Objectives
-
•Describe the differences between solids, liquids, and gases.
7.5-1. Viscosity
Viscosity, which is the resistance of liquids to flow, depends upon the energy of interaction relative to thermal energy. In order for a liquid to flow, molecules must slide past one another, breaking and forming intermolecular interactions. If thermal energy is relatively low compared to the energy of interaction, flow is retarded and the liquid is viscous because the molecules cannot readily break the interactions. Thus, viscosity decreases as the liquid is heated. Viscosity also depends upon the shape of the molecule: viscosity increases as the ease with which molecules become entangled increases.7.5-2. Surface Tension
Molecules in a liquid minimize their energy by minimizing their surface area, and the surface tension is the energy required to increase the surface area of a liquid by a fixed amount.
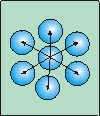
Figure 7.15a: Surface Tension
Molecules in bulk of a liquid experience forces in all directions, which cancel one another. Thus, there is no net force acting on the molecule.
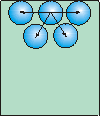
Figure 7.15b: Surface Tension
There are no molecules above one at the surface so there is no upward force to cancel the downward force. Thus, there is a net inward force exerted on molecules at the surface that causes liquid to minimize its surface area.
7.5-3. Meniscus
A meniscus is concave when the adhesive forces between a liquid and its container are strong, but it is convex when they are weak.

Figure 7.16a: Meniscus
Glass contains many Si–O bonds, and water can hydrogen bond to the oxygens on the surface of the wall. The strong adhesive forces between water and glass tend to draw the liquid up the walls of the glass and produce the concave shape of the meniscus.

Figure 7.16b: Meniscus
Mercury atoms do not interact well with glass, so the adhesive forces are very weak. Consequently, mercury forms a convex meniscus to maximize Hg-Hg interactions and minimize interactions with the walls of the container.
7.5-4. Summary of Properties
It is the interplay between thermal energy and the energy of interaction that dictates the state of a substance.
| Gas | Liquid | Solid | |
| Shape | shape and volume of the container | shape of the bottom of container, but have own volume | own shape and volume |
| Intermolecular Distance | great enough that intermolecular forces can be neglected | much smaller in a liquid than in a gas | similar to those in a liquid, but the molecules are oriented so as to optimize their interactions |
| Thermal vs. Interaction Energy | thermal >> interaction | thermal ~ interaction | thermal << interaction |
| Molecular Motion | straight line until a collision | random but restricted | oscillations about fixed positions |
Table 7.3: A Comparison of the Gas, Liquid, and Solid States
7.6 Changes in State
Introduction
We have all seen ice melt and liquid water boil as a result of increasing the temperature, but ice can also be melted by applying pressure, and liquid water can be made to boil by reducing the pressure. Thus, ice melts under a skater's weight, and water that boils in Denver will not boil at the same temperature at sea level. In this section, we discuss the various changes in state at a molecular level.Prerequisites
-
•1.7 Energy (Distinguish between kinetic and potential energy.)
-
•7.3 Intermolecular Interactions (Distinguish between intermolecular and intramolecular forces.)
Objectives
-
•Order the three states of matter in terms of their potential energies.
-
•Distinguish between the thermal energy and potential energy of interaction of a molecule.
-
•Define heat of fusion, heat of vaporization, and heat of sublimation.
-
•Define fusion.
-
•Describe melting and freezing at a molecular level.
-
•Define melting point.
-
•Predict whether the solid or liquid state is more dense from the slope of the solid
 line in a plot of P vs. T for the substance.
line in a plot of P vs. T for the substance.
-
•Define vapor pressure.
-
•Define boiling point and explain what is meant by the normal boiling point.
-
•Use a plot of vapor pressure versus temperature to determine whether a substance is a liquid or a vapor at a given set of conditions of T and P.
-
•Determine which of two substances has the stronger intermolecular forces based on their vapor pressures at some temperature or their boiling points at some pressure.
-
•Predict which of two compounds is expected to show stronger dispersion forces.
-
•Predict relative boiling points based on the relative strengths of the dispersion forces of the molecules.
-
•Explain the effect of permanent dipoles on boiling points.
-
•Explain the effect of hydrogen bonding on boiling points.
-
•Explain why bubbles form at the boiling point.
-
•Define sublimation and deposition.
-
•Use a phase diagram to determine which state of matter a substance is in at given conditions of temperature and pressure.
-
•Use a phase diagram to determine the melting point, the normal boiling point, and the triple point of a substance.
-
•Use a phase diagram to determine the vapor pressure at a given temperature or the temperature at which the vapor pressure has a given value.
Introductory Overview
7.6-1. Video on the Molecular View of Changes in State
View a video describing changes in state using kinetic molecular theory.- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
Energy Considerations
7.6-2. Heats of Change
The potential energy of a particle varies as solid < liquid << gas.
-
•the interactions in a solid are so strong that the solid has its own shape;
-
•the interactions in the liquid are not strong enough to retain a unique shape, but they are strong enough to keep the liquid in the bottom of the container and adopting that shape; and
-
•the interactions in gases are so weak that the molecules fill the container.
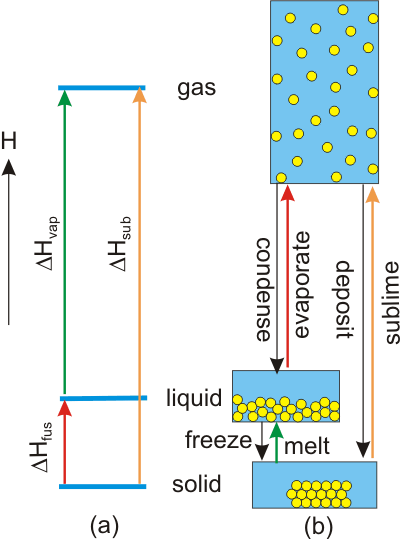
Figure 7.17: Relative Energies of the Vapor, Liquid, and Solid States
The solid and liquid states have similar energies, but the energy of the vapor is much higher.
7.6-3. Heats of State Changes Defined
The heats of fusion, vaporization, and sublimation are always positive.
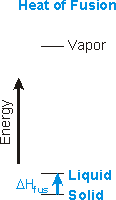
Figure 7.18a: Heat of Fusion
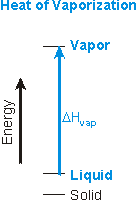
Figure 7.18b: Heat of Vaporization
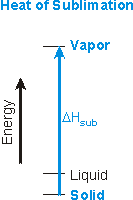
Figure 7.18c: Heat of Sublimation
Solid-Liquid Equilibria
7.6-4. Solid-Liquid Equilibria
The melting point is the temperature at which the solid and liquid are in equilibrium.

Figure 7.19
7.6-5. Graph of Solid-Liquid Equilibrium
The more dense phase can be determined from the slope of the P vs. T line for the solid-liquid equilibrium.
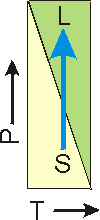
Figure 7.20a: Melting Point as a Function of Pressure
The slope of the line is negative, so increasing the pressure (indicated by the arrow) on the solid-liquid equilibrium converts the solid into the liquid (melts the solid). In this case, the liquid is the more dense state, which is the situation for water.
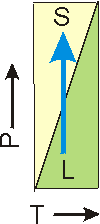
Figure 7.20b: Melting Point as a Function of Pressure
The slope of the line is positive, so increasing the pressure on the solid-liquid equilibrium converts liquid into solid (freezes the liquid). In this case, the solid is more dense than the liquid. This is the more common situation.
Liquid-Vapor Equilibria
7.6-6. Liquid-Vapor Equilibria
Vapor pressure increases with temperature and decreases with the strength of the intermolecular force.

Figure 7.21
7.6-7. Vapor Pressure of Water, Dew Point, and Relative Humidity
Table 7.4 gives the vapor pressure of water at various temperatures. Note that the vapor pressure increases with temperature, as it must for all substances. Weather reports normally indicate the partial pressure of water in the atmosphere in terms of the relative humidity or dew point. The relative humidity is 100% times the ratio of the observed partial pressure of water in the atmosphere to the vapor pressure of water at that temperature. The dew point is the temperature at which the atmospheric water would begin to condense, i.e., the temperature at which the vapor pressure of H2O equals its partial pressure in the atmosphere.Example:
For example, consider a day on which the temperature is 25 °C and the partial pressure of H2O is 12.8 torr. We note from Table 7.4 that the vapor pressure of water is 12.8 torr at 15 °C, so 15 °C is the dew point. The vapor pressure of water at 25 °C is 23.8 torr, so:
For example, consider a day on which the temperature is 25 °C and the partial pressure of H2O is 12.8 torr. We note from Table 7.4 that the vapor pressure of water is 12.8 torr at 15 °C, so 15 °C is the dew point. The vapor pressure of water at 25 °C is 23.8 torr, so:
relative humidity =
(100%) = 53.8%
 |
| 12.8 |
| 23.8 |
 |
| T (°C) |
P (torr) |
T (°C) |
P (torr) |
|
|---|---|---|---|---|
| 0 | 4.6 | 50 | 92.5 | |
| 5 | 6.5 | 55 | 118.0 | |
| 10 | 9.2 | 60 | 149.4 | |
| 15 | 12.8 | 65 | 187.5 | |
| 20 | 17.5 | 70 | 233.7 | |
| 25 | 23.8 | 75 | 289.1 | |
| 30 | 31.8 | 80 | 355.1 | |
| 35 | 41.2 | 85 | 433.6 | |
| 40 | 55.3 | 90 | 525.8 | |
| 45 | 71.9 | 95 | 633.9 |
Table 7.4: Vapor Pressure of Water at Various Temperatures
7.6-8. Graph of Liquid-Vapor Equilibrium
The vapor pressure of a compound at a given temperature depends upon the strengths of its intermolecular interactions. Compounds with stronger intermolecular interactions have lower vapor pressures than those that interact only weakly because stronger interactions favor the more condensed state. Figure 7.22 shows the vapor pressure of CCl4 and H2O as a function of temperature. From the graph, we can see that the vapor pressure of CCl4 is 760 torr at 77 °C, while H2O must be heated to 100 °C to obtain the same vapor pressure. We also note that the vapor pressure of H2O is less than that of CCl4 at every temperature, so the intermolecular interactions are stronger in H2O. Although the dispersion forces are greater in CCl4, water also has dipolar and hydrogen bonding forces, which results in its relatively low vapor pressure.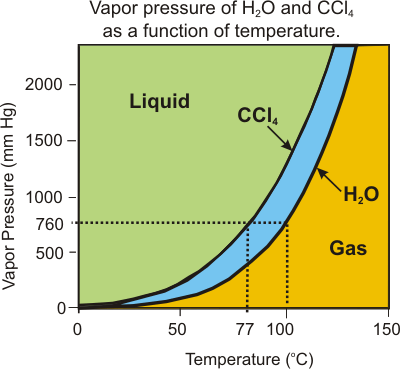
Figure 7.22: Vapor Pressure of CCl4 and H2O as a Function of Temperature
Both substances are liquids at temperatures and pressures in the green region and both are gases at conditions in the orange region. CCl4 is a gas while H2O is a liquid in the blue region.
7.6-9. Boiling Points
Molecules with sufficient kinetic energy escape into the gas phase if they are on the surface of the liquid, but what about those that are not on the surface? The highly energetic molecules in the bulk of the liquid also attempt to escape into the gas by aggregating into bubbles, but the bubbles cannot withstand pressures greater than the vapor pressure of the gas at that temperature, so the bubbles cannot form if the external pressure exceeds the vapor pressure. However, the bubbles are sustained at the temperature where the vapor pressure of the liquid equals the external pressure, so we define the boiling point as that temperature at which the vapor pressure equals the external pressure. A liquid can be made to boil at other temperatures by reducing the external pressure to the vapor pressure of the liquid at that temperature, so Table 7.4 and Figure 7.22 can also be viewed as the boiling points as a function of pressure. Thus, the boiling point of water at 4.6 torr is 0 °C, and at 23.8 torr, it is 25 °C. Typically, substances are boiled in a container open to the atmosphere, so the external pressure is 1 atm, and it is this boiling point that is assumed when a boiling point is given without reference to a pressure. We define the normal boiling point as the boiling point at 1 atm pressure. Whenever the boiling point of a substance is given without reference to an external pressure, it is assumed to be the normal boiling point. The normal boiling point of water is100 °C.
7.6-10. Normal Boiling Points and Intermolecular Interactions
The higher the boiling point of a substance, the stronger are its intermolecular interactions.
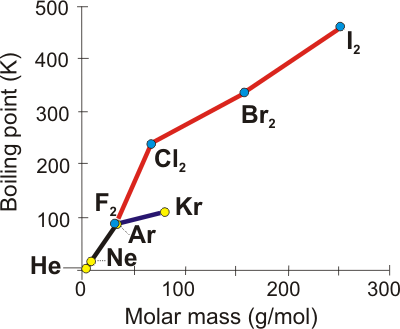
Figure 7.23: Boiling Points of the Halogens and the Noble Gases
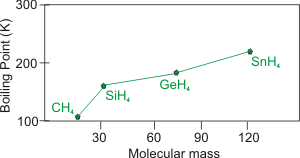
Figure 7.24a: Boiling Points of the Group 4 Hydrides as a Function of Molar Mass
Group 4A: None of the hydrides of Group 4A exhibit hydrogen bonding, so their boiling points decrease as their molar masses decrease.
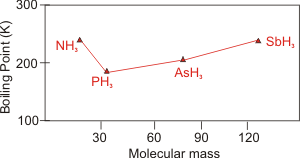
Figure 7.24b: Boiling Points of the Group 5 Hydrides as a Function of Molar Mass
Group 5A: Dispersion forces are the main differences between the intermolecular forces of SbH3, AsH3, and PH3, so their boiling points decrease with decreasing molar mass. However, NH3 exhibits hydrogen bonding, so its high boiling point is much higher than would be predicted based on the boiling points of the other members of the group.
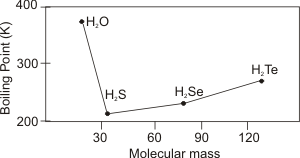
Figure 7.24c: Boiling Points of the Group 6 Hydrides as a Function of Molar Mass
Group 6A: Water can hydrogen bond through two hydrogen atoms. Consequently, its boiling point is much higher than that of H2S, which has stronger dispersion forces. Based solely on molar mass, water would be predicted to boil around 200 K rather than 373 K. Thus, water would be a gas rather than a liquid at normal conditions on Earth if it were not for the hydrogen bond.
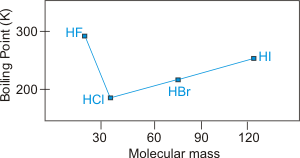
Figure 7.24d: Boiling Points of the Group 7 Hydrides as a Function of Molar Mass
Group 7A: Note that HF exhibits hydrogen bonding, but, based on the above graph, HCl does not. Chlorine is electronegative enough, but it is too large.
7.6-11. Predicting Relative Boiling Points Exercise
Exercise 7.11:



Indicate the molecule with the higher boiling point in each pair.
-
N2
-
CO Both molecules have the same molar mass, so the dispersion forces are similar. However, N2 is not polar, while CO is. Therefore, CO is predicted to have a higher boiling point because the dipole-dipole interactions are in addition to the dispersion forces.

-
CH2Cl2 Both molecules have the same molar mass, so the dispersion forces are similar. However, CF4 is not polar, so it has only dispersion forces, while CH2Cl2 is polar and displays both dispersion and dipole-dipole forces. Consequently, CH2Cl2 is predicted to have a higher boiling point because it has the stronger intermolecular interactions.
-
CF4

-
CS2 The molecules are both linear and are therefore not polar, so neither displays dipole-dipole interactions. The molar mass of CS2 is greater than that of CO2, so CS2 is predicted to have a higher boiling point due to stronger dispersion forces.
-
CO2

7.6-12. Critical Point
Liquid-vapor equilibria, like the one shown for CCl4 and H2O in Figure 7.22, are established in closed containers (the liquid would evaporate before establishing equilibrium in an open container). However, as the liquid-vapor equilibrium is heated, the density of the liquid decreases, while the density of the gas increases. At a temperature known as the critical temperature, Tc, the densities are the same, there is no longer a boundary between the two phases, and the liquid-vapor line ends. The pressure at this point is called the critical pressure, Pc. The point established by the critical temperature and pressure is called the critical point. Thus, the critical temperature is the highest temperature at which the liquid phase can exist, and the critical pressure is the pressure required to liquefy a gas at the critical temperature. The critical temperature is also a function of intermolecular forces and increases in the same manner as the boiling point. Above the critical point, the substance is neither a gas nor a liquid and has properties of both phases. Under these conditions, the substance is a supercritical fluid.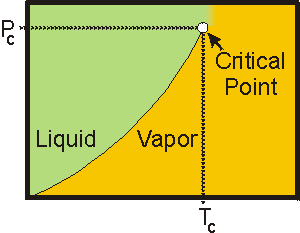
Figure 7.25
Solid-Vapor Equilibria
7.6-13. Solid-Vapor Equilibria
Under certain conditions, the vapor and solid states are in equilibrium. Sublimation is the process in which a solid is converted directly to a gas. The reverse process is called deposition. Ice sublimes slowly, which is why snow can disappear without melting when the temperature does not rise above 0 °C. A dynamic equilibrium is established when the rate of sublimation equals the rate of deposition.
Figure 7.26
 vapor equilibrium is established. Increasing the temperature increases the pressure of vapor above a solid, i.e., it causes the solid to sublime. Increasing the pressure of the gas at a point on the line causes more solid to deposit.
vapor equilibrium is established. Increasing the temperature increases the pressure of vapor above a solid, i.e., it causes the solid to sublime. Increasing the pressure of the gas at a point on the line causes more solid to deposit.
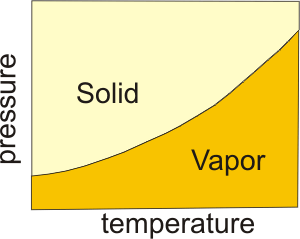
Figure 7.27: Sublimation Pressure as a Function of Temperature
Phase Diagrams
7.6-14. Phase Diagram of Water
A phase diagram shows the stable phases of a substance as a function of temperature and pressure. For example, consider the phase diagram of water shown in Figure 7.28. The lines separating the states represent the equilibria discussed in the previous sections.-
•Point A is on the solid
 liquid line. The pressure is 1 atm, or 760 torr, so the temperature (0 °C) is called the normal melting point, or simply the melting point. Increasing the pressure at point A moves the system into the liquid region (melts the solid), so liquid water is more dense than ice (the reason ice floats).
liquid line. The pressure is 1 atm, or 760 torr, so the temperature (0 °C) is called the normal melting point, or simply the melting point. Increasing the pressure at point A moves the system into the liquid region (melts the solid), so liquid water is more dense than ice (the reason ice floats).
-
•Point B is the triple point, which is the temperature and pressure at which all three states of matter coexist. The triple point of water is 0.0098 °C and 4.58 torr (0.006 atm). Reducing the pressure at this point would cause the ice water to boil.
-
•Point C represents room conditions (P = 760 torr and T = 298 K (25 °C)). It is well within the liquid range for water, consistent with water being a liquid under these conditions. However, in a closed container there would also be 24 torr (0.031 atm) of vapor above the liquid. If the pressure over the liquid were reduced to 24 torr at this temperature, the water would boil.
-
•Point D is on the liquid
 vapor line. The pressure is 760 torr, so the temperature (100 °C) is the normal boiling point. Increasing the temperature or decreasing the pressure drives the system into the vapor region, while decreasing the temperature or increasing the pressure of vapor causes steam to condense.
vapor line. The pressure is 760 torr, so the temperature (100 °C) is the normal boiling point. Increasing the temperature or decreasing the pressure drives the system into the vapor region, while decreasing the temperature or increasing the pressure of vapor causes steam to condense.
-
•Point E is the critical point. The critical temperature is Tc = 374 °C, and the critical pressure is Pc = 218 atm. Water is a supercritical fluid above this point.
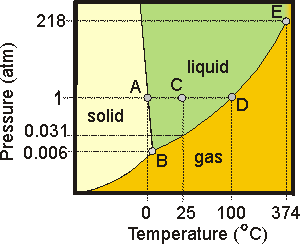
Figure 7.28: Phase Diagram of Water
The above phase diagram shows how the state of matter of water varies with conditions of temperature and pressure. Water is a solid in the yellow region, a liquid in the green region, and a gas or vapor in the orange region. The temperatures and pressures are not to scale.
7.6-15. Phase Diagram of Carbon Dioxide
Consider the phase diagram of CO2 shown in Figure 7.29.-
•Point A is on the solid
 vapor line and is the point where the partial pressure of the vapor in equilibrium with the solid is 1 atm. Thus, CO2 can be liquified at 1 atm by reducing its temperature to –78 °C.
vapor line and is the point where the partial pressure of the vapor in equilibrium with the solid is 1 atm. Thus, CO2 can be liquified at 1 atm by reducing its temperature to –78 °C.
-
•Point B is the triple point (5.1 atm and –56 °C).
-
•Point C represents room conditions. CO2 is a gas under these conditions.
-
•Point D shows that CO2 can be liquified at room temperature (25 °C) by increasing the pressure to 67 atm.
-
•Point E is the critical point. The critical temperature is Tc = 31 °C, and the critical pressure is Pc = 73 atm. Supercritical CO2 is used as a dry cleaning solvent.
 liquid line indicates that the solid is more dense than the liquid. Finally, carbon dioxide does not have a normal boiling point because the liquid does not exist at pressures below 5.1 atm (the triple point pressure).
liquid line indicates that the solid is more dense than the liquid. Finally, carbon dioxide does not have a normal boiling point because the liquid does not exist at pressures below 5.1 atm (the triple point pressure).
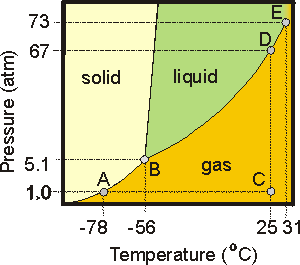
Figure 7.29: Phase Diagram of Carbon Dioxide
7.6-16. Phase Diagram Exercise
Exercise 7.12:





In the following exercises, give all temperatures to the nearest 25 °C and all pressures to the nearest
0.1 atm.
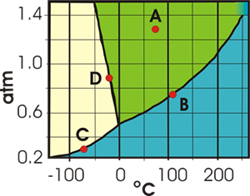
0.1 atm.

What is the normal boiling point of X in °C?
175___
The normal boiling point is the temperature at which the vapor pressure is 1 atm, which is
175 °C in the above graph. °C
175 °C in the above graph. °C
What is the melting point of X in °C?
-25___
The melting point is the temperature at which solid and liquid are in equilibrium at 1 atm pressure, which is –25 °C in the above graph.
°C

What is the temperature in °C at the triple point?
0___
The triple point is the temperature and pressure where the solid, liquid, and vapor are all in equilibrium. The temperature where this occurs in the above phase diagram is 0 °C.
°C

What is the pressure in atm at the triple point?
0.5___
The triple point is the temperature and pressure where the solid, liquid, and vapor are all in equilibrium. The pressure where this occurs in the above phase diagram is 0.5 atm.
atm

-
What state of matter is X in at point A?
-
solid
-
liquid The substance is in the liquid region at point A.
-
gas

-
What is the most dense state of X?
-
solid
-
liquid Increasing the pressure on the solid-liquid line moves the substance into the liquid region, so the liquid is the most dense state.
-
gas

What is the critical temperature of X in °C?
250___
The critical temperature is the temperature at the critical point, which is the end of the liquid-vapor line. In this example, it occurs at 250 °C.
°C

What is the critical pressure of X in atm?
1.4___
The critical pressure is the pressure at the critical point, which is the end of the liquid-vapor line. In this example, it occurs at 1.2 atm.
atm

Indicate the phase change that is caused by each of the following.
-
increasing T at point B
-
vaporization Increasing the temperature at point B moves the substance into the vapor region. Therefore, the substance vaporizes.
-
condensation Increasing the temperature moves the substance from the liquid-vapor line into the vapor region.
-
sublimation Increasing the temperature moves the substance from the liquid-vapor line into the vapor region.
-
deposition Increasing the temperature moves the substance from the liquid-vapor line into the vapor region.
-
melting Increasing the temperature moves the substance from the liquid-vapor line into the vapor region.
-
freezing Increasing the temperature moves the substance from the liquid-vapor line into the vapor region.

-
increasing T at point C
-
vaporization Increasing the temperature moves the substance from the solid-vapor line into the vapor region.
-
condensation Increasing the temperature moves the substance from the solid-vapor line into the vapor region.
-
sublimation Increasing the temperature moves the substance from the solid-vapor line into the vapor region, so the substance sublimes.
-
deposition Increasing the temperature moves the substance from the solid-vapor line into the vapor region.
-
melting Increasing the temperature moves the substance from the solid-vapor line into the vapor region.
-
freezing Increasing the temperature moves the substance from the solid-vapor line into the vapor region.

-
increasing P at point D
-
vaporization Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region.
-
condensation Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region.
-
sublimation Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region.
-
deposition Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region.
-
melting Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region, so the substance melts.
-
freezing Increasing the pressure moves the substance from the solid-liquid equilibrium into the liquid region.