Chapter 10 – Solutions
Introduction
Solutions are homogeneous mixtures, i.e., mixtures whose properties are uniform throughout. Solutions are all around us. We live in a solution of gases called the atmosphere. A carbonated beverage is a solution of a gas in a liquid. Brass and solder are solutions of a solid in a solid. Solutions that are predominately water are called aqueous solutions. Drinks, blood, and the ocean are all aqueous solutions. All of the reactions we discuss at the end of this chapter and in the following two chapters take place in aqueous solutions, and an understanding of solutions is necessary to understanding these reactions. In this chapter, we examine the properties of solutions, predict whether one substance will dissolve in another, and discuss the nature of aqueous solutions of ionic substances.10.1 Concentration
Introduction
The properties of a solution made from substances A and B depend upon the dominant type of interaction in the solution. The dominant interaction, A-A, B-B, or A-B, depends upon the relative number of each type of molecule, which is given by their concentrations. If the concentration of A is much greater than that of B, then A-A interactions dominate, and the solution properties are similar to those of A. Thus, the concentration of each substance in a solution is an important property of the solution. Although there are many ways to express concentration, we focus on the most common form used in the chemistry laboratory in this section.Prerequisites
Objectives
-
•Define the terms solution, solvent, and solute.
-
•Distinguish between homogeneous and heterogeneous mixtures.
-
•Determine the molarity of a solution given the amount of solute a given volume of solution contains.
-
•Determine the volume required to deliver a given number of moles of solute or the number of moles of solute in a given volume of a solution of known molarity.
10.1-1. Definitions
Solutions involving liquids are comprised of a solvent and at least one solute.
| homogeneous mixture | Homogeneous mixtures are mixtures that have constant composition throughout. A mixture made by mixing water and alcohol or by dissolving sugar in water is homogeneous because the alcohol, sugar, and water molecules are dispersed evenly throughout the mixture. Thus, the ratio of sugar or alcohol molecules to water molecules is the same no matter the location or size of the sample. Consequently, the properties of the mixture are also the same throughout. |
| heterogeneous mixture | Heterogeneous mixtures do not have uniform composition. Mixing table salt and sugar or water and oil produces a heterogeneous mixture because the properties of a sample of the mixture can vary from those of one substance to those of the other. |
| solution | A solution is a homogeneous mixture. A mixture of water and alcohol is a solution, as is a mixture made by dissolving sugar in water. |
| solvent | The component of a solution that dictates the phase of a solution. Water is the most common solvent. If more than one liquid is present, the liquid in greater amount is usually considered to be the solvent, but water is sometimes considered the solvent even if it is not present in the greatest amount. |
| solute | A solute is a component of a solution that is not the solvent. A solution is made by dissolving one or more solutes in a solvent. |
| concentration | The concentration of a solute is the ratio that relates the amount of the solute to the amount of either the solvent or the entire solution. |
Table 10.1: Some Definitions
10.1-2. Molarity
The molarity of a solute is the number of moles of that solute per liter of solution.
10.1-3. Molarity Exercise
Exercise 10.1:
100 mL of solution contains 4.8 g sugar. What is the molar concentration of sugar (sucrose) in the solution [C12H22O11]? How many mL of this solution would contain 0.0030 mol C12H22O11?
1. First compute the molar mass of sugar.
342___
Mm = (12 mol C)(12 g/mol) + (22 mol H)(1 g/mol) + (11 mol O)(16 g/mol) = 342 g/mol
g/mol

2. Next, determine the number of moles of sugar.
0.014___

4.8 g sugar ×
= 0.014 mol sugar
mol sugar
| 1 mol sugar |
| 342 g sugar |
3. Determine the molarity of the sugar as the number of moles of sugar divided by the number of liters of solution in which it is dissolved.
0.14___

M =
=
= 0.14 M
M
| mol sugar |
| liters of solution |
| 0.014 mol sugar |
| 0.100 L solution |
4. Use the molarity and the desired number of moles to determine the volume of solution required.
21___
moles of solute divided by molarity of solution = volume of solution mL sol'n
0.0030 mol C12H22O11 ×
×
= 21 mL sol'n
| 1 L of sol'n |
| 0.14 mol C12H22O11 |
| 1000 mL sol'n |
| 1 L sol'n |
moles of solute divided by molarity of solution = volume of solution mL sol'n
10.1-4. Solute to Solvent Ratio
Most of the solutions that we encounter are aqueous solutions, and their properties depend upon the ratio of solute to water particles. In this section, we examine the ratio of solute and solvent particles in a typical aqueous solution. We can determine the number of moles of solute present in a given volume of solution of known molarity, but, in order to determine the number of moles of solvent in a liter of solution, we must know the density of the solution, i.e., we must know the mass of a unit volume of the solution. The density of water is 1.0 g/mL, or 1.0 g/cm3. The density of a solution that is predominately water will be close to that of pure water.10.1-5. Solution Exercise
Exercise 10.2:
How many water molecules are present for each sugar molecule (C12H22O11, Mm = 342 g/mol) in a
0.1 M aqueous solution of sugar? Assume that the density of the solution is the same as pure water
(1.0 g/mL).
0.1 M aqueous solution of sugar? Assume that the density of the solution is the same as pure water
(1.0 g/mL).
Solution: We need to determine the ratio of moles of sugar to moles of water. We know there is 0.10 mol of sugar in a liter of solution, so we need to determine how many moles of water are in a liter of solution, which we can get from the mass of water in the solution since the mass of the solution = mass of water + mass of sugar.
1. First, we determine the mass of 1.0 L of solution.
1000___

1 L soln ×
×
= 1000 g soln
g soln
| 1000 mL soln |
| 1 L soln |
| 1 g soln |
| 1 mL soln |
2. Next, compute the mass of sugar in 1.0 L of solution.
34.2___

1 L soln ×
×
= 34.2 g sugar
g sugar
| 0.10 mol sugar |
| 1 L soln |
| 342 g sugar |
| 1 mol sugar |
3. Next, determine the mass of water in 1.0 L of solution.
966___
The mass of solution equals the mass of water plus the mass of sugar, so
mass of water = mass of solution – mass of sugar = 1000 g – 34 g = 966 g water. g H2O
mass of water = mass of solution – mass of sugar = 1000 g – 34 g = 966 g water. g H2O
4. Now, determine the number of moles of water in 1.0 L of solution.
53.7___

966 g H2O ×
= 53.7 mol H2O
mol H2O
| 1 mol H2O |
| 18.0 g H2O |
5. Finally, determine the ratio of water molecules to sugar molecules in the 0.10 M solution.
537___
1.0 L of a 0.10 M solution contains 0.10 mol sugar and 53.7 mol water, so 
ratio =
= 537 mol H2O/mol C12H22O11.
There are 537 water molecules for every sugar molecule.
mol water/mol sugar
| 53.7 mol H2O |
| 0.1 mol C12H22O11 |
The properties of the solution are much more like those of water than those of sugar because there are so many more water molecules present. Indeed, this is why the density of the solution is nearly the same as that of pure water.
10.2 Solution Process
Introduction
In this section, we break the solution process into steps and examine the energy requirements of each step.Prerequisites
-
•9.2 Enthalpy (definition of enthalpy)
-
•9.7 Free Energy (relationship between the standard free energy and the extent of a process)
-
•9.11 Equilibrium and the Equilibrium Constant
-
•9.5 Entropy (meaning of entropy)
Objectives
-
•Define the term solubility.
-
•Explain the three events involved in dissolving one substance in another and predict the sign of the enthalpy change for each.
10.2-1. Solubility
A substance is usually soluble when ΔH° of solution is negative or only slightly positive.
-
•soluble: A solute is soluble if its solubility is at least 0.1 M.
-
•slightly soluble: Substances with solubilities between 0.01 M and 0.1 M are slightly soluble.
-
•insoluble: Substances with solubilities less than 0.01 M are insoluble.
-
•miscible: Two liquids that are completely soluble in one another are said to be miscible. For example, alcohol and water are miscible, but water and gasoline are not.
| Substance | Solubility in Water at 25 °C |
Description | Substance | Solubility in Water at 25 °C |
Description | |
|---|---|---|---|---|---|---|
| NaCl | 6 M | soluble | CaSO4 | 0.02 M | slightly soluble | |
| MgO | 0.0003 M | insoluble | CuS | 10–18 M | insoluble |
Table 10.2: Some Solubilities
A solution in which the solute concentration is equal to its solubility is said to be saturated. When excess solid is added to a saturated solution, an equilibrium is established between the solid and the dissolved solute. For example, the following equilibrium is established when an excess of NaCl solid is added to water.
NaCl(s)  NaCl(aq)
NaCl(aq)
 NaCl(aq)
NaCl(aq)10.2-2. Solution Process for Dissolving a Polar Solute in H2O
To form a solution, the solute particles must be separated, cavities must be created in the solvent, and the solute particles must enter the cavities.
-
•ΔHsolute is the energy required to separate the solute particles.
-
•ΔHsolvent is the energy required to create the cavities in the solvent that will accommodate the solute particles.
-
•ΔHmixing is the energy change produced when the solute particles enter the cavities in the solvent.
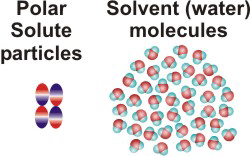
Figure 10.1a: Solution Process: Initial Conditions
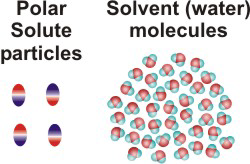
Figure 10.1b: Solution Process: ΔHsolute
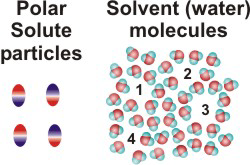
Figure 10.1c: Solution Process: ΔHsolvent
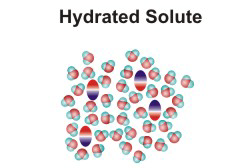
Figure 10.1d: Solution Process: ΔHmixing
10.2-3. Solvation
Solvation involves the creation of cavities in the solvent and solute particles entering those cavities.
-
•Ionic and polar solutes are soluble in polar solvents.
-
•Nonpolar molecules are soluble in nonpolar solvents.
10.2-4. Like Dissolves Like Exercise
Exercise 10.3:



Use the rule that like dissolves like to answer the following.
-
Which of the following is more soluble in water?
-
HBr HBr is polar while Br2 is not. Polar substances are more soluble in polar solvents like water, so HBr is more soluble in water.
-
Br2 Br2 is not polar but water is. Nonpolar molecules are not soluble in polar solvents like water.

-
Which of the following is a better solvent for I2?
-
CS2 I2 is not polar, so it is more soluble in nonpolar solvents. CS2 is linear and nonpolar, so CS2 is the better solvent for I2.
-
H2O I2 is not polar, so it is more soluble in nonpolar solvents. H2O is very polar. I2 is not very soluble in water.

-
In which of the following solvents would KCl be more soluble?
-
CCl4
-
H2O KCl is ionic, and ionic substances are more soluble in polar solvents like water. CCl4 is tetrahedral and nonpolar, so KCl is more soluble in water.

10.3 Organic Compounds
Introduction
We concluded the last section with "like dissolves like." That is, polar solutes tend to be soluble in polar solvents such as water, while nonpolar molecules tend to be soluble in nonpolar solvents and insoluble in polar solvents such as water. However, large molecules can have both polar and nonpolar regions. In this section, we examine the solubility of such molecules in water.Prerequisites
Objectives
-
•Distinguish between hydrophobic and hydrophilic and explain the hydrophobic effect.
-
•Relate the solubility of a substance in water to the relative sizes of its hydrophilic and hydrophobic regions.
10.3-1. Organic Compounds
Regions of a molecule that interact well with water are hydrophilic, while regions that do not are hydrophobic.
10.3-2. Hydrophobic and Hydrophilic Examples
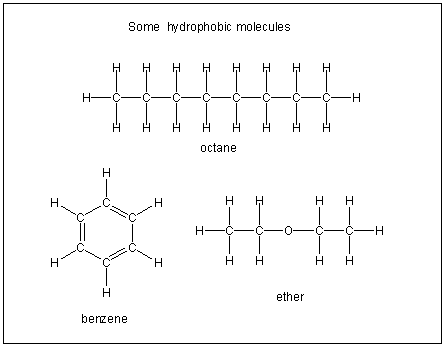
Figure 10.2a: Hydrophobic Molecules
Hydrophobic molecules are not soluble in water because they contain many C–H bonds and are not very polar.
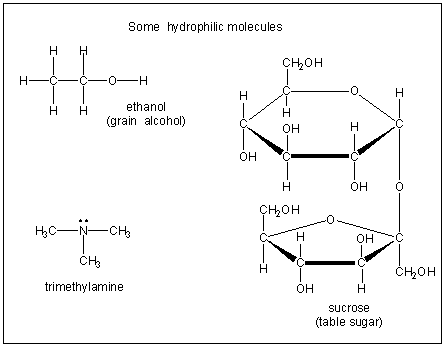
Figure 10.2b: Hydrophilic Molecules
Hydrophilic compounds are water soluble because they contain O–H groups or a nitrogen lone pair that can interact strongly with water.
10.3-3. Acetone
Acetone, (CH3)2C=O, is a common laboratory solvent because many organic substances are soluble in it, and it is miscible with water. Acetone contains CH3 groups that interact with other organic compounds through dispersion forces, so many organic substances dissolve in acetone. However, it also contains a polar C=O group, which makes the molecule hydrophilic. As with alcohols, the water solubility of compounds like this depends upon the lengths of the carbon chains; as the hydrophobic portion of the molecule increases, its solubility in water decreases. For example, (CH3CH2CH2CH2)2C=O is only slightly soluble in water.
Figure 10.3: Ball-and-Stick Model of Acetone
10.3-4. Alcohols
The solubility of alcohols decreases as the hydrophobic region gets larger.
| Solvent | ||
|---|---|---|
| Alcohol | H2O | C6H14 |
| CH3OH | ∞ | 0.12 M |
| CH3CH2OH | ∞ | ∞ |
| CH3(CH2)2OH | ∞ | ∞ |
| CH3(CH2)3OH | 0.91 M | ∞ |
| CH3(CH2)4OH | 0.31 M | ∞ |
| CH3(CH2)5OH | 0.059 M | ∞ |
| CH3(CH2)6OH | 0.015 M | ∞ |
Table 10.3: Solubilities of Some Alcohols
10.3-5. Ether or Water Exercise
Ether is a common solvent that contains hydrophobic regions and is not very polar, but water is a very polar solvent with no hydrophobic regions.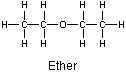
Figure 10.4
Exercise 10.4:


Are each of the following more soluble in water or in ether?
-
water Decane is a hydrophobic molecule with no hydrophilic (polar) regions. Consequently, it is soluble in ether but not in water.
-
ether
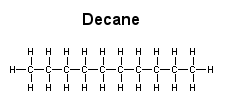

-
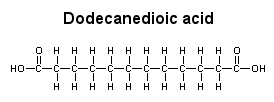
water Dodecanedioic acid has two hydrophilic regions, the COOH groups at either end, and it also has a large hydrophobic region (ten CH2 groups) in the center. In this case, the hydrophobic region dominates, and the acid is soluble in ether, but not in water.
-
ether

10.4. Detergents and Micelles
Introduction
Grease and stains are hydrophobic, but we remove them by washing our dishes and clothing in water. We can do this because of the special properties of detergents, the topic of this section.Prerequisites
Objectives
-
•Describe a detergent and identify its head and tail.
-
•Describe monolayers and explain why they form.
-
•Describe micelles and explain how they function to dissolve hydrophobic materials in water.
10.4-1. Detergents and Soaps
Detergents and soaps each have a hydrophilic (polar) head and a long hydrophobic tail.
-
1space-filling
-
2ball-and-stick
-
3condensed structure that does not show C–H bonds explicitly
-
4common abbreviation that is a skeletal drawing that indicates carbon atoms in the tail as the junction of two or more lines; the polar head is represented by a circle
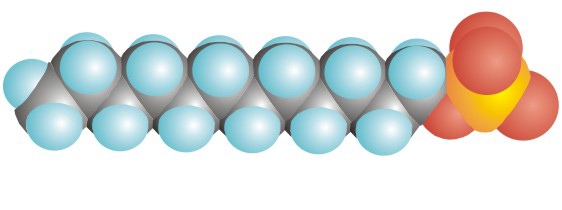
Figure 10.5a: Space-Filling Representation of SDS, a Detergent
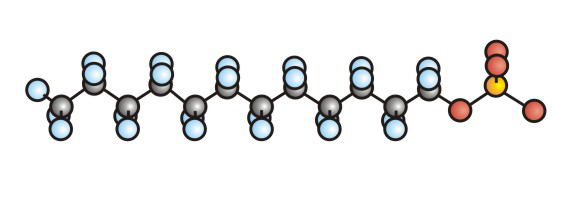
Figure 10.5b: Ball-and-Stick Representation of SDS, a Detergent
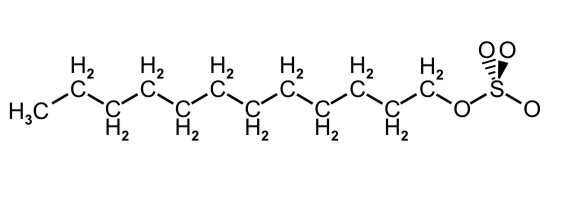
Figure 10.5c: Condensed Structure Representation of SDS, a Detergent
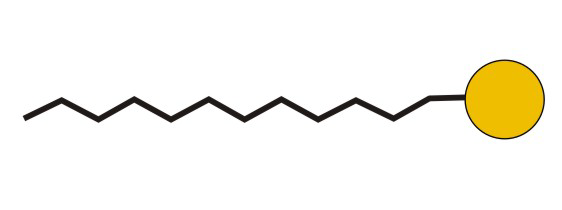
Figure 10.5d: Common Abbreviation Representation of SDS, a Detergent
10.4-2. Monolayers
At low concentrations, detergents form monolayers in which the tails extend out of solution.

Figure 10.6: SDS Monolayer
At small concentrations, SDS forms a monolayer (a layer that is one molecule thick) on the surface of the water. The hydrophobic tails stick up out of the water, while the hydrophilic heads enter the water.
10.4-3. Micelles
Micelles, which are composed of many detergent molecules, contain a hydrophobic center and a hydrophilic shell.
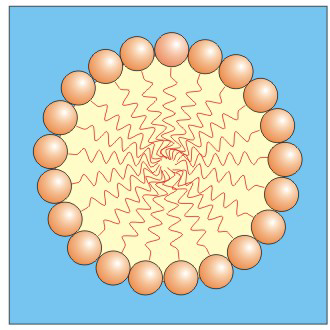
Figure 10.7: A Cross-Sectional View of a Micelle
The polar heads are in direct contact with the aqueous environment and form a spherical shell around the hydrophobic interior.
10.5 Electrolytes
Introduction
Ionic compounds are not soluble in most solvents, but water is so polar that some ionic compounds do dissolve in it. Blood contains many ions, and the concentrations of those ions are critical to our well-being. Ions in water are responsible for water "hardness." In this section, we examine the nature of aqueous solutions of ionic compounds.Prerequisites
Objectives
-
•Indicate whether a substance is an electrolyte or a nonelectrolyte.
10.5-1. Definitions
Aqueous solutions of electrolytes conduct electricity due to the presence of ions in solution. Ionic compounds, acids, and bases are electrolytes.
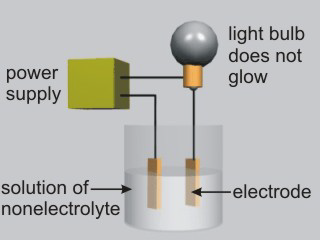
Figure 10.8a: Solutions of Nonelectrolytes Do Not Conduct Electricity
-
•Molecular compounds that are not acids or bases are nonelectrolytes. H2O and most organic compounds are nonelectrolytes.
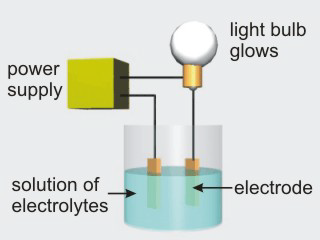
Figure 10.8b: Solutions of Electrolytes Do Conduct Electricity
-
•Ionic compounds dissolve to produce metal cations and nonmetal anions. The ions can also be derived from polyatomic ions, such as ammonium or sulfate ions.
-
•Acids are compounds that produce H1+ when they dissolve in water. Production of the H1+ also produces a cation. For example, an aqueous solution of HCl is hydrochloric acid: HCl → H1+ + Cl1–. Since ions are produced when acids dissolve in water, acids are electrolytes. However, not all hydrogen-containing compounds are acids. Acids are those compounds whose formulas begin with an H. For example, HNO3, HClO4, and H2SO4 are some other common acids, while CH4 is not an acid.
| Solution | Glow | Solution Type | Solution Particles |
|---|---|---|---|
| water | none | nonelectrolyte | H2O molecules |
| table salt | bright | strong electrolyte | Na1+ + Cl1– ions |
| HCl | bright | strong electrolyte | HCl → H1+ + Cl1– is extensive. |
| HF | dim | weak electrolyte | HF → H1+ + F1– is NOT extensive. |
| table sugar | none | nonelectrolyte | C12H22O11 molecules |
| NaNO3 | bright | strong electrolyte | Na1+ + NO31– ions |
| NaOH | bright | strong electrolyte | Na1+ + OH1– ions |
| rubbing alcohol | none | nonelectrolyte | C3H5OH molecules |
| ammonia | dim | weak electrolyte | NH3 + H2O → NH41+ + OH1– is NOT extensive. |
Table 10.4: Conduction Properties of Some Aqueous Solutions
10.5-2. Ionic Compounds as Electrolytes
Ionic compounds are strong electrolytes, so when a solid ionic compound is dissolved in water, it goes into solution completely as ions. We will no longer use (aq) to indicate that an ion is in solution because isolated ions in chemcial equations are always in solution. Consider the following dissociations.NaCl(s) → Na1+ + Cl1− MgCl2(s) → Mg2+ + 2 Cl1− K2S(s) → 2 K1+ + S2−
NaNO3(s) → Na1+ + NO31– MgSO4(s) → Mg2+ + SO42– K3PO4 → 3 K1+ + PO43–
10.5-3. Acids and Bases as Electrolytes
Ionic compounds are not the only class of compounds that are electrolytes; acids and bases are electrolytes as well. The first chemical definition of acids and bases was made by Svante Arrhenius. An Arrhenius acid is a substance that produces H1+ ions when dissolved in water, and an Arrhenius base is a substance that produces OH1– ions when dissolved in water. Acids can be identified because the acidic protons are usually written first in their chemical formulas. For example, H2S is an acid, so the protons appear first in its formula, but NH3 is not, so the protons do not appear first in its formula. In Arrhenius theory, acids ionize in water in a manner similar to ionic substances, but only strong acids ionize completely. The common strong acids are HCl, HBr, HI, HNO3, HClO4, and H2SO4. For example, the following chemical equations represent the Arrhenius view of dissolving three strong acids in water.HCl(g) → H1+ + Cl1– HNO3(l) → H1+ + NO31– HClO4(l) → H1+ + ClO41–
HF(aq)  H1+ + F1– HNO2(aq)
H1+ + F1– HNO2(aq)  H1+ + NO21– HClO2(aq)
H1+ + NO21– HClO2(aq)  H1+ + ClO21–
H1+ + ClO21–
 H1+ + F1– HNO2(aq)
H1+ + F1– HNO2(aq)  H1+ + NO21– HClO2(aq)
H1+ + NO21– HClO2(aq)  H1+ + ClO21–
H1+ + ClO21–NaOH(s) → Na1+ + OH1− Ba(OH)2(s) → Ba2+ + 2 OH1−
F1– + H2O  HF(aq) + OH1– NO21– + H2O
HF(aq) + OH1– NO21– + H2O  HNO2(aq) + OH1–
HNO2(aq) + OH1–
 HF(aq) + OH1– NO21– + H2O
HF(aq) + OH1– NO21– + H2O  HNO2(aq) + OH1–
HNO2(aq) + OH1– NH3(aq) + H2O  NH41+ + OH1–
NH41+ + OH1–
 NH41+ + OH1–
NH41+ + OH1–10.5-4. Nonelectrolytes
Nonelectrolytes retain their molecular identity in solution.
C12H22O11(s) → C12H22O11(aq)
10.5-5. Distinguishing Strong Electrolytes and Nonelectrolytes Exercise
Exercise 10.5:







Indicate whether each substance is an electrolyte or a nonelectrolyte.
-
H2O
-
electrolyte
-
nonelectrolyte

Water is a nonelectrolyte. The light bulb does not glow, which means that the particles in liquid water are predominantly H2O molecules, not ions.

-
C12H22O11
-
electrolyte
-
nonelectrolyte

Like most organic compounds, sugar is a nonelectrolyte. The light bulb does not glow, which means that the sugar particles in solution are C12H22O11 molecules.

-
NaCl
-
electrolyte

NaCl is an electrolyte, as are all ionic compounds. The light bulb glows, which means that an aqueous solution of sodium chloride consists of Na1+ and Cl1– ions, not NaCl molecules. -
nonelectrolyte

-
NaNO3
-
electrolyte

NaNO3 is an electrolyte because it is ionic. Charge flows through the solution, so an aqueous solution of sodium nitrate consists of Na1+ and NO31– ions, not NaNO3 molecules. -
nonelectrolyte

-
HCl
-
electrolyte

HCl is an electrolyte because it is an acid. The light bulb glows, so the particles in solution are H1+ and Cl1– ions. However, the H–Cl bond is covalent, so HCl is not an ionic compound. According to the Arrhenius definition, acids are substances that contain H atoms and produce H1+ ions when added to water. Acids can be identified from their chemical formula because the H is written first. Thus, HCl is an acid, but NH3 is not. -
nonelectrolyte

-
NaOH
-
electrolyte

NaOH is an electrolyte. The solution conducts electricity, so the particles in solution are Na1+ and OH1– ions. NaOH is an Arrhenius base, i.e., a substance that produces hydroxide ions when added to water. -
nonelectrolyte

-
CH3OH
-
electrolyte
-
nonelectrolyte

CH3OH is a nonelectrolyte. No charge flows through the solution, so the particles in solution are CH3OH molecules, not ions. Note that CH3OH contains H atoms and an OH group, but it is neither an Arrhenius acid (see HCl) nor an Arrhenius base (see NaOH). It is an organic molecule, and organic molecules are not ordinarily electrolytes.

10.5-6. Distinguishing Strong and Weak Electrolytes Exercise
Exercise 10.6:




Indicate whether each substance is a strong electrolyte or a weak electrolyte.
-
H2SO3
-
strong H2SO3 is an acid, but it is not one of the six strong acids.
-
weak

-
HNO3
-
strong
-
weak HNO3 is one of the six strong acids.

-
KF
-
strong
-
weak F1– is a weak base, but KF is an ionic compound.

-
NH3
-
strong NH3 is a weak base.
-
weak

10.5-7. Ion Concentrations in Solutions of Strong Electrolytes
Ionic compounds, such as NaCl, are strong electrolytes because all of the solid NaCl that dissolves dissociates into ions. Thus, a solution labeled 0.10 M NaCl contains Na1+ and Cl1– ions, but no NaCl molecules. The ions react independently of one another; a chloride ion in a solution of NaCl is the same as one in a solution of KCl or MgCl2. Thus, it is the concentration of the ion, not the parent compound, that is important in solution chemistry. To convert from the concentration of the parent compound to that of any ion requires the stoichiometry of the chemical equation for the dissociation, which is given by the stoichiometry of the compound.Example:
For example, to determine the concentration of chloride ions in a 0.10 M MgCl2 solution, we recognize that there are two moles of chloride ions for every one mole of MgCl2 and write the following.
An aqueous solution that is labeled 0.10 M MgCl2 is 0.10 M in Mg2+ ions and 0.20 M in Cl1– ions, but it contains no MgCl2!
For example, to determine the concentration of chloride ions in a 0.10 M MgCl2 solution, we recognize that there are two moles of chloride ions for every one mole of MgCl2 and write the following.
[Cl1−] =
×
=
= 0.20 M
| 0.10 mol MgCl2 |
| 1 L solution |
| 2 mol Cl1− |
| 1 mol MgCl2 |
| 0.20 mol Cl1− |
| 1 L solution |
10.5-8. Ion Concentration Exercise
Exercise 10.7:
What are the concentrations of the ions in the following solutions?
0.0364 M BaCl2


[
Ba2+]
=
0.0364___
[Ba2+] =
×
=
= 0.0364 M
M
| 0.0364 mol BaCl2 |
| 1 L solution |
| 1 mol Ba2+ |
| 1 mol BaCl2 |
| 0.0364 mol Ba2+ |
| 1 L solution |
[
Cl1–]
=
0.0728___
[Cl1−] =
×
=
= 0.0728 M
M
| 0.0364 mol BaCl2 |
| 1 L solution |
| 2 mol Cl1− |
| 1 mol BaCl2 |
| 0.0728 mol Cl1− |
| 1 L solution |
0.108 M K3PO4


[
K1+]
=
0.324___
[K1+] =
×
=
= 0.324 M
M
| 0.108 mol K3PO4 |
| 1 L solution |
| 3 mol K1+ |
| 1 mol K3PO4 |
| 0.324 mol K1+ |
| 1 L solution |
[
PO43–]
=
0.108___
[K1+] =
×
=
= 0.108 M
M
| 0.108 mol K3PO4 |
| 1 L solution |
| 1 mol PO43− |
| 1 mol K3PO4 |
| 0.108 mol PO43− |
| 1 L solution |
10.6 Electrolyte Solutions
Introduction
Electrolytes are hydrated in aqueous solution. In this section, you can view an animation showing a crystal of NaCl dissolving in water.Objectives
-
•Describe how a crystal of sodium chloride dissolves in water.
10.6-1. The Water Dipole
Ionic bonds must be broken when an ionic substance dissolves, but ionic bonds are strong interactions, so ΔHsolute is large and positive. Thus, ΔHsolvation, the enthalpy of solvation (hydration in this case because the solvent is water), must be large and negative for an ionic substance to dissolve in water. In other words, the interaction between the water molecules and the ions must be very strong. This strong interaction arises because water has a strong dipole, which points from the center of the hydrogen atoms toward the electronegative oxygen atom. The large dipole of water also increases its dielectric constant (ε in Coulomb's Law), so water effectively shields each ion from the charge of surrounding ions.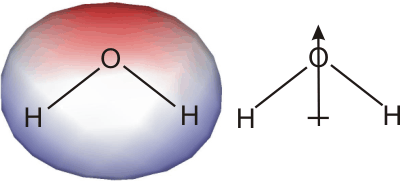
Figure 10.9: Water Dipole
10.6-2. The Solution Process
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.

Figure 10.10: Dissolving Sodium Chloride in Water
-
•The sodium and chloride ions in a crystal adopt the sodium chloride structure with each sodium ion (represented by the blue spheres) surrounded by six chloride ions (represented by the green spheres) and each chloride ion surrounded by six sodium ions. Water is a very polar molecule with the center of positive charge residing between the two hydrogen atoms, and the negative charge centered on the oxygen atom. Only a small fraction of the water molecules are shown. There would be hundreds of water molecules for each ion in a typical solution, and the water molecules would be in contact with each other.
-
•The positive ends of the water dipoles interact with the chloride anions (green) on the surface of the crystal, while the negative ends interact with the sodium cations (blue) at the surface. The interactions are sufficiently strong to pull the ions on the surface of the crystal out into the solution.
-
•Six strongly interacting water molecules solvate (or hydrate in this case) each chloride ion in solution. There are many layers of water molecules around each ion. Note that the positive end of the dipole of each water molecule faces the chloride ion.
-
•The sodium ion is hydrated in the same manner as the chloride ion, except that it is the negative end of the water dipole that faces the cation. As in the case of the anion, the cation is surrounded by several layers of water molecules. The two oppositely charged ions do not recombine because the dipoles of the intervening water molecules arrange themselves in such a way as to insulate the two charges.
10.7 Dissolution of Ionic Substances
Introduction
Not all ionic substances are soluble in water. Indeed, most are not. In this section, we examine the factors that dictate the solubility of ionic substances in water and develop some simple rules to help us predict solubilities.Prerequisites
-
•1.8 Electromagnetism and Coulomb's Law (Describe the factors that dictate the force of attraction of two opposite charges suspended in some medium.)
-
•4.5 Polyatomic Ions (Identify polyatomic ions.)
Objectives
-
•Relate solubility to the charge on the ions.
10.7-1. Dissolution and Coulomb's Law
The process whereby an ionic substance dissolves in water is called dissolution. The chemical equation for the dissolution of calcium carbonate is CaCO3(s) → Ca2+ + CO32–. As an approximation, we assume that an ionic substance is soluble when the force of attraction between its ions in solution is small enough that the ions can exist separately in solution, i.e., the force is not great enough that the separated ions attract one another to reverse the dissolution process. The force of attraction is described by Coulomb's Law. Although the solubility of ionic compounds is more complicated than a simple Coulombic attraction of the ions, we can still use Coulomb's Law to understand the process qualitatively by examining the factors that dictate the strength of the force of attraction. Thus, an ionic compound is likely soluble in water if the following are true.-
•r is very large. r is a property of the solution because it is the distance between the ions in the solution. r depends only upon concentration; ions in concentrated solutions are closer than ions in dilute solutions. If a substance is soluble, then the force of attraction cannot be great even at moderate concentration, so r cannot be very large.
-
•ε is large. ε is the dielectric constant of the solvent and measures how well the solvent screens the charges in solution. The dielectric constant of water is about 40 times greater than that of a nonpolar solvent such as hexane (C6H14). This means that the force of attraction of two oppositely charged ions separated by the same distance is 40 times greater in C6H14 than in water, so the ions are much less likely to recombine in water. The dielectric constants of several common solvents are given in Table 10.5.
-
•q1q2 is small. The product of the charges on the ions is the only factor that is a property of the ionic solute. Recall that the charges on ions typically fall in the range of –3 to +3; thus, q1q2 lies between 1 and 9. If the magnitude of the charge on either ion is 1, the magnitude of q1q2 cannot exceed 3, but if neither charge is 1, then the magnitude of q1q2 cannot be less than 4. Consequently, we expect that ionic compounds containing highly charged ions will not be as soluble in water as those containing +1 and –1 ions because the force of attraction between highly charged ions is too strong.
In general, ionic substances that contain a +1 and/or a –1 ion are more soluble than those that do not.
| Solvent Name | Formula | ε | Solvent Name | Formula | ε | |
|---|---|---|---|---|---|---|
| acetic acid | CH3COOH | 6.20 | acetone | (CH3)2C=O | 21.0 | |
| benzene | C6H6 | 2.28 | carbon disulfide | CS2 | 2.63 | |
| carbon tetrachloride | CCl4 | 2.24 | dimethyl sulfoxide | (CH3)2S=O | 47.2 | |
| ether | (C2H5)2O | 4.27 | ethanol | C2H5OH | 25.3 | |
| hexane | C6H14 | 1.89 | methanol | CH3OH | 33.0 | |
| water | H2O | 80.10 | ||||
Table 10.5: Dielectric Constants of Selected Solvents at 20 °C
10.7-2. Dissolution and Coulomb's Law Exercise
Exercise 10.8:



Use the rule that compounds with lower q1q2 products are more soluble than those with high q1q2 products to select the more soluble compound in each pair.
-
CsI q1q2 = –1 for CsI. This is the lowest possible magnitude, and CsI is very soluble in water.
-
AlPO4 q1q2 = (+3)(–3) = –9 for AlPO4. This is the largest possible magnitude because the magnitude of the charge on an ion seldom exceeds 3. Thus, AlPO4 is insoluble in water.

-
CaS The magnitude of q1q2 is
(2)(2) = 4 for CaS, which is the same as for MgO. CaS, like MgO, is insoluble in water. -
NH4NO3 The magnitude of q1q2 is
(1)(1) = –1 for NH4NO3, which is the same as for NaCl. NH4NO3, like NaCl, is very soluble in water.

-
CaCl2 The magnitude of
q1q2 = (2)(1) = 2 for a Ca2+-Cl1– interaction, which is less than the 6 obtained for the Al3+-O2– interaction. CaCl2 is soluble in water. -
Al2O3 The magnitude of q1q2 is
(3)(2) = 6 for a Al3+-O2– interaction, which is greater than the 2 obtained for the Ca2+-Cl1– interaction. Al2O3 is insoluble in water.

10.7-3. Solubility Rules
The solubility rules offer only a rough guideline to the solubility of ionic compounds; there are many exceptions.
| Rule 1 | Compounds of NH41+ and Group 1A ions are soluble. | Compounds containing a +1 and/or –1 ion are probably soluble. Hydroxides (OH1–) are insoluble except by Rule 1, so they are a common exception. |
| Rule 2 | Compounds of NO31–, ClO41–, ClO31–, and C2H3O21– are soluble. | |
| Rule 3 | Compounds of Cl1–, Br1–, and I1– are soluble except those of Ag1+, Cu1+, Tl1+, Hg22+, and Pb2+. | The insoluble halides appear to violate the +1/–1 rule for solubility, but these metals are late metals that are fairly electronegative, so their halides are not very ionic. For example, the Ag–Cl bond is only 30% ionic, and the Pb–Cl bond is only 15% ionic (see Chapter 5.2-5 Exceptions). Consequently, Coulomb's Law doesn't really apply here. |
| Rule 4 | Compounds of SO42– are soluble except those of Ca2+, Sr2+, Ba2+, and Pb2+. | Sulfates are the only soluble compounds that do not have to contain an +1 or –1 ion. |
| Rule 5 | Most others are NOT soluble in water. | If an ionic substance is not soluble by Rules 1 through 4, then it is probably not soluble in water. |
Table 10.6: Solubility Rules for Ionic Substances in Water
10.7-4. Solubility is a Matter of Degree
Solubilities vary from very soluble to very insoluble, but no ionic solid is completely soluble in water and none is completely insoluble. As is usually the case in chemistry, it is a matter of degree. Consider the following solubilities of some sulfates.| Compound | Molar Solubility |
| BaSO4 | 0.000013 |
| PbSO4 | 0.00014 |
| SrSO4 | 0.00073 |
| Hg2SO4 | 0.00010 |
| CaSO4 | 0.015 |
| Ag2SO4 | 0.027 |
| Al2(SO4)4 | 1.1 |
| FeSO4 | 1.9 |
| MgSO4 | 3.0 |
| MnSO4 | 4.2 |
Table 10.7
In general, the solubilities in Table 10.7 are consistent with the solubility rules. However, our definition of soluble was that the solubility of the substance had to be at least 0.1 M, and a slightly soluble substance had to have a solubility between 0.01 and 0.1 M, so the following are inconsistencies in the solubility rules.
-
•CaSO4 is slightly soluble, not insoluble.
-
•Ag2SO4 is slightly soluble, not soluble.
-
•Hg2SO4 is insoluble, not soluble.
10.7-5. Predicting Solubility Exercise
Exercise 10.9:


-
Which of the following compounds can be used to make a solution that is 0.1 M in Pb2+ ions?
-
PbSO4 PbSO4 is not soluble. (Rule 4)
-
Pb(NO3)2 Pb(NO3)2 is soluble. (Rule 2)
-
PbI2 PbI2 is not soluble. (Rule 3)
-
Pb(OH)2 PbOH2 is not soluble. (Rule 5)

-
Which of the following compounds can be used to make a solution that is 0.1 M in CrO42– ions?
-
K2CrO4 K2CrO4 is soluble. (Rule 1)
-
BaCrO4 BaCrO4 is not soluble. (Rule 5)
-
FeCrO4 FeCrO4 is not soluble. (Rule 5)
-
Ag2CrO4 Ag2CrO4 is not soluble. (Rule 5)

10.8 Precipitation of Ionic Substances
Introduction
Most reactions between ionic compounds take place in aqueous solutions, but not all of the species present in the solutions necessarily take part in the reactions. A net ionic equation, or simply net equation, is one that shows only those ions that are involved in the reaction. In this section, we learn how to predict which ions are involved in precipitation reactions and how to write net ionic equations for their reaction.Prerequisites
Objectives
-
•Write the net ionic equation for a simple precipitation reaction.
-
•Use the solubility rules to predict whether an ionic compound is expected to be soluble in water.
-
•Write a net ionic equation for the precipitation of an ionic compound from solution.
-
•Use the solubility rules to predict whether mixing two solutions will produce a precipitate.
10.8-1. Formation of AgCl
A net ionic equation shows only the ions involved in the precipitation. Spectator ions are not included.
-
•Na1+ + NO31–
-
•Ag1+ + Cl1–
| Ag1+ + Cl1– | → | AgCl |
 |
→ |  |
| The aqueous solution on the right contains Ag1+ and NO31– ions. The aqueous solution on the left contains Na1+ and Cl1– ions. | → | NaNO3 is soluble by Rules 1 and 2, and AgCl is insoluble by Rule 3. Thus, mixing the two solutions produces a solution of Na1+ and NO31– ions as well as a white precipitate of AgCl. |
10.8-2. Video on the AgCl Precipitation Process
The precipitation of AgCl
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
-
•When the two cations or the two anions encounter one another, the force is repulsive.
-
•When Ag1+ and NO31– encounter one another, the force of attraction is weak enough that the shielding of the intervening water molecules (dielectric) prevents reaction.
-
•When Ag1+ encounters Cl1–, the driving force to form a bond (mostly covalent in nature) is sufficient to overcome the shielding from water, and AgCl precipitates from solution.
10.8-3. Predicting a Precipitate
Exercise 10.10:

Write the net ionic equation that describes the formation of a yellow precipitate when solutions of lead acetate and potassium iodide are mixed.
 |
→ |  |
| K1+ + I1– and Pb2+ + C2H3O21– | → | ? |
-
First, determine which pair of ions reacts.
-
Pb2+ + K1+ Combinations between ions of like charge can be ignored.
-
Pb2+ + I1– PbI2 is insoluble by Rule 3, so there is a reaction between Pb2+ and I1–.
-
C2H3O21– + Cl1– Combinations between ions of like charge can be ignored.
-
C2H3O21– + K1+ This combination produces a soluble substance according to both Rules 1 and 2.

Write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)
o_Pb^2+_s

+ One PbI2 contains 2 iodide ions, so a coefficient of "2" must be placed in front of the I1– to balance the equation.
| Pb2+ | + | 2 I1− | → | PbI2 |
| Cation | + | Anion | → | Precipitate |
o_2I^1-_s

→ One PbI2 contains 2 iodide ions, so a coefficient of "2" must be placed in front of the I1– to balance the equation.
| Pb2+ | + | 2 I1− | → | PbI2 |
| Cation | + | Anion | → | Precipitate |
o_PbI_2_s

One PbI2 contains 2 iodide ions, so a coefficient of "2" must be placed in front of the I1– to balance the equation.
| Pb2+ | + | 2 I1− | → | PbI2 |
| Cation | + | Anion | → | Precipitate |
10.8-4. Practice
Exercise 10.11:






Use the method developed previously and Table 10.6 to determine whether a reaction occurs when aqueous solutions containing the following are mixed. If a reaction does occur, write the balanced equation.
-
Select the reacting ions or "no reaction."
-
Na1+ + Ag1+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
Na1+ + NO31– There is no reaction between Na1+ + NO31–, see Rules 1 and 2.
-
PO43– + Ag1+

According to Rule 5, there is a reaction between PO43– + Ag1+. Silver phosphate is a yellow solid. -
PO43– + NO31– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction Try again, there is a reaction.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_3Ag^1+_s
3 Ag1+ + PO43– → Ag3PO4

+
o_PO_4^3-_s
3 Ag1+ + PO43– → Ag3PO4

→
o_Ag_3PO_4_s
3 Ag1+ + PO43– → Ag3PO4

-
Select the reacting ions or "no reaction."
-
NH41+ + Na1+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
NH41+ + PO43– There is no reaction between NH41+ + PO43– according to Rule 1.
-
SO42– + Na1+ There is no reaction between SO42– + Na1+ according to Rules 1 and 4.
-
SO42– + PO43– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction

There is no reaction as evidenced by the clear solution that results.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_NONE_ins
There is no reaction.

+
o_NONE_ins
There is no reaction.

→
o_NONE_ins
There is no reaction.

-
Select the reacting ions or "no reaction."
-
Pb2+ + K1+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
Pb2+ + CrO42–

There is a reaction between Pb2+ and CrO42– using Rule 5. Lead chromate is a yellow solid. -
NO31– + K1+ There is no reaction between NO31– and K1+ because of Rules 1 and 2.
-
NO31– + CrO42– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction Try again, there is a reaction.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_Pb^2+_s
Pb2+ + CrO42– → PbCrO4(s)

+
o_CrO_4^2-_s
Pb2+ + CrO42– → PbCrO4(s)

→
o_PbCrO_4_s
Pb2+ + CrO42– → PbCrO4(s)

-
Select the reacting ions or "no reaction."
-
Ba2+ + NH41+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
Ba2+ + SO42–

There is a reaction between Ba2+ and SO42–, based on Rule 4. Barium sulfate is a white solid. -
C2H3O21– + NH41+ There is no reaction between C2H3O21– and NH41+, according to Rules 1 and 2.
-
C2H3O21– + SO42– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction Try again, there is a reaction.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_Ba^2+_s
Ba2+ + SO42– → BaSO4

+
o_SO_4^2-_s
Ba2+ + SO42– → BaSO4

→
o_BaSO_4_s
Ba2+ + SO42– → BaSO4

-
Select the reacting ions or "no reaction."
-
Co2+ + Na1+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
Co2+ + PO43–

There is a reaction between Co2+ and PO43–, see Rule 5. Cobalt(II) phosphate is a purple solid. -
Cl1– + Na1+ There is no reaction between Cl1– and Na1+ because of Rules 1 and 3.
-
Cl1– + PO43– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction Try again, there is a reaction.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_3Co^2+_s
3 Co2+ + 2 PO43– → Co3(PO4)2

+
o_2PO_4^3-_s
3 Co2+ + 2 PO43– → Co3(PO4)2

→
o_Co_3(PO_4)_2_s
3 Co2+ + 2 PO43– → Co3(PO4)2

-
Select the reacting ions or "no reaction."
-
NH41+ + Ag1+ The pair must contain an anion (negative charge) and a cation (positive charge).
-
NH41+ + NO31– There is no reaction between NH41+ and NO31– based on Rules 1 and 2.
-
SO42– + Ag1+ There is no reaction between SO42– and Ag1+ because of Rule 4.
-
SO42– + NO31– The pair must contain an anion (negative charge) and a cation (positive charge).
-
no reaction

There is no reaction as is shown by the clear solution that is produced.

If there is a reaction, write the balanced equation (Cation + Anion → Precipitate). (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces. Enter NONE in each answer box if there is no reaction.)
o_NONE_ins
There is no reaction.

+
o_NONE_ins
There is no reaction.

→
o_NONE_ins
There is no reaction.

10.9 Solubility Equilibria
Introduction
A precipitate is in equilibrium with its ions in solution, and, in this section, we show how to treat that equilibrium quantitatively.Prerequisites
-
•9.11 Equilibrium and the Equilibrium Constant (Write the equilibrium constant expression for a reaction involving solids and solutes.)
Objectives
-
•Write the chemical equation to which the solubility product constant applies and write the solubility product constant expression for a compound.
-
•Determine the concentration of an ion in equilibrium with another ion of known concentration in a saturated solution of a compound composed of the ions.
10.9-1. Solubility Equilibria
When the amount of solid that is added to water exceeds the amount that is soluble in water at that temperature, the solid reaches equilibrium with the ions. For example, when solid AgCl is added to water, only a small amount of the solid dissolves as it reaches equilibrium with its ions.AgCl(s)  Ag1+ + Cl1−
Ag1+ + Cl1−
 Ag1+ + Cl1−
Ag1+ + Cl1−Ksp = [Ag1+][Cl1−] = 1.8 × 10−10
| Compound | Ksp expression | Ksp value |
|---|---|---|
| AgCl | [Ag1+][Cl1–] | 1.8 × 10–10 |
| Ag2CrO4 | [Ag1+]2[CrO42–] | 1.1 × 10–12 |
| AgI | [Ag1+][I1–] | 8.3 × 10–17 |
| Ag2S | [Ag1+]2[S2–] | 6.3 × 10–50 |
| Ag3PO4 | [Ag1+]3[PO43–] | 2.6 × 10–18 |
Table 10.8: Solubility Product Constant Values and Expressions for Some Compounds of Silver
10.9-2. Exercise
Exercise 10.12:
The solubility product constant is given for a substance, but it applies to a process. Check your understanding by answering the following questions.
- Ksp of zinc carbonate is 1.0 x 10–10.
Write the process to which this number applies. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)

o_ZnCO_3_s
Process: ZnCO3  Zn2+ + CO32–
Zn2+ + CO32–

 Zn2+ + CO32–
Zn2+ + CO32–

o_Zn^2+_s
Process: ZnCO3  Zn2+ + CO32–
Zn2+ + CO32–

+  Zn2+ + CO32–
Zn2+ + CO32–
o_CO_3^2-_s
Process: ZnCO3  Zn2+ + CO32–
Zn2+ + CO32–

 Zn2+ + CO32–
Zn2+ + CO32–
Write the expression to which it applies. Specify the cation concentration first in the expression. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)
Ksp =
o_[Zn^2+][CO_3^2-]_s
Ksp = [Zn2+][CO32–] = 1.0 × 10–10

- Ksp of iron(III) hydroxide is 1.6 × 10–39.
Write the process to which this number applies. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)

o_Fe(OH)_3_s
Process: Fe(OH)3  Fe3+ + 3 OH1–
Fe3+ + 3 OH1–

 Fe3+ + 3 OH1–
Fe3+ + 3 OH1–

o_Fe^3+_s
Process: Fe(OH)3  Fe3+ + 3 OH1–
Fe3+ + 3 OH1–

+  Fe3+ + 3 OH1–
Fe3+ + 3 OH1–
o_3OH^1-_s
Process: Fe(OH)3  Fe3+ + 3 OH1–
Fe3+ + 3 OH1–

 Fe3+ + 3 OH1–
Fe3+ + 3 OH1–
Write the expression to which it applies. Specify the cation concentration first in the expression. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)
Ksp =
o_[Fe^3+][OH^1-]^3_s
Ksp = [Fe3+][OH1–]3 = 1.6 × 10–39

10.9-3. Determining Equilibrium Concentrations
Exercise 10.13:
Solubility product constants can be used to determine the equilibrium concentrations of the ions present. The following example shows how this is done.
What is maximum [Fe3+] that can exist in a solution in which [OH1–] = 1.0 × 10–7 M?
- The Ksp of iron(III) hydroxide is 1.6 × 10–39.
First, write the process to which the solubility product constant applies. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)

o_Fe(OH)_3_s
Fe3+ + 3 OH1–  Fe(OH)3
Fe(OH)3

 Fe(OH)3
Fe(OH)3

o_Fe^3+_s
Fe3+ + 3 OH1–  Fe(OH)3
Fe(OH)3

+  Fe(OH)3
Fe(OH)3
o_3OH^1-_s
Fe3+ + 3 OH1–  Fe(OH)3
Fe(OH)3

 Fe(OH)3
Fe(OH)3
Next, write the solubility product constant expression for the process with the cation concentration specified first. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a carat (^). For example, NH_4^1+ for NH41+. Omit any spaces.)
Ksp =
o_[Fe^3+][OH^1-]^3_s
Ksp = [Fe3+][OH1–]3

Substitute the known values for Ksp and [OH1–] into the solubility product constant expression and solve for [Fe3+].
o_1.6e-18_s

[Fe3+] =
=
= 1.6 × 10−18 M
M
| Ksp |
| [OH1−]3 |
| 1.6 × 10−39 |
| (1.0 × 10−7)3 |







