Chapter 3 – Atomic Structure and Properties
Introduction
The nuclear atom and quantum theory are the accepted theories for the atom. In this chapter, we demonstrate their utility by using them to explain trends in atomic properties.3.1 Valence Electrons
Introduction
Most of the properties of an atom are related to the nature of its electron cloud and how strongly the electrons interact with the nucleus. In this section, we identify the electrons that are most important in determining atomic properties.Prerequisites
-
•2.7 Electron Configurations (Write electron configurations for atoms.)
Objectives
-
•Distinguish between core and valence electrons.
-
•Determine the number of valence electrons in an atom.
-
•Write valence electron configurations of main group atoms.
3.1-1. Valence Electrons Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
3.1-2. Valence Electron Definition
Valence electrons consist of those electrons in the outermost s sublevel and those in any unfilled sublevel.
-
•Core electrons are the tightly bound electrons that are unaffected by chemical reactions. Core electrons reside in filled sublevels and form a spherical shell of negative charge around the nucleus that affects the amount of nuclear charge that the outermost electrons experience.
-
•Valence electrons are those outermost electrons that dictate the properties of the atom and are involved in chemical bonding. The valence electrons are those in the outermost s sublevel and any unfilled sublevels.
The number of valence electrons in an atom equals the group number of the atom.
3.1-3. Valence Electron Configurations of Main Group Elements
All of the elements in a group have the same number of valence electrons (Group number), and their valence electron configurations are the same except for the value of the n quantum number (the period). Thus, the periodicity of chemical properties is due to the periodicity of the valence electron configurations. The table shows the generic valence electron configurations of the elements in each group of the main group elements and the specific configurations of the second period.| Group | 1A | 2A | 3A | 4A | 5A | 6A | 7A |
| Configuration | ns1 | ns2 | ns2np1 | ns2np2 | ns2np3 | ns2np4 | ns2np5 |
| 2nd Period Element | Li | Be | B | C | N | O | F |
| Configuration | 2s1 | 2s2 | 2s22p1 | 2s22p2 | 2s22p3 | 2s22p4 | 2s22p5 |
Table 3.1: Valence Electron Configurations
3.1-4. Valence Electron Configurations of Transition Elements
The valence electron configuration of the first row transition elements has the form 4s23db, where b is the position of the element in the d block. Cr and Cu are the two exceptions because they each promote one of their 4s electrons into the 3d sublevel to obtain half-filled and completely filled 3d sublevels. Zinc is often considered a transition element because of its location, but its d sublevel is full, and its chemistry is more like that of a Group 2A metal than a transition metal. Thus, its valence electron configuration is 4s2, in keeping with its Group number of 2B. Similarly, Cu is 4s13d10, and the fact that it is a 1B element would lead you to think that its valence electron configuration should be 4s1. However, unlike zinc, copper does use its d orbitals in bonding. Indeed, the most common ion formed by copper is the Cu2+ ion. Thus, copper's chemistry is dictated by its d electrons, and its valence electron configuration is 4s13d10.3.1-5. Practice with Valence Electrons
Valence electrons and valence electron configurations are very important in chemistry. Practice determining the valence electron configurations for atoms and then check your answer by clicking on the element in the periodic table below.| 1 1A |
2 2A |
3 3B |
4 4B |
5 5B |
6 6B |
7 7B |
8 8B |
9 8B |
10 8B |
11 1B |
12 2B |
13 3A |
14 4A |
15 5A |
16 6A |
17 7A |
18 8A |
| H |
He |
||||||||||||||||
| Li |
Be |
B |
C |
N |
O |
F |
Ne |
||||||||||
| Na |
Mg |
Al |
Si |
P |
S |
Cl |
Ar |
||||||||||
| K |
Ca |
Sc |
Ti |
V |
Cr |
Mn |
Fe |
Co |
Ni |
Cu |
Zn |
Ga |
Ge |
As |
Se |
Br |
Kr |
| Rb |
Sr |
||||||||||||||||
3.1-6. Core vs. Valence Electrons Exercise
Exercise 3.1:
Use the facts that all of the electrons in an atom are either core or valence electrons, and the number of valence equals the group number of the
element to determine the number of valence and core electrons in each of the following atoms.
O
Valence =
6___
Oxygen is 1s2 2s2 2p4. The valence
electrons are the four in the unfilled sublevel (2p) and the two in the
outermost s sublevel (2s), so oxygen has six valence electrons: 2 + 4.
Alternatively, oxygen is a 6A nonmetal, so it contains six
valence electrons.

Core =
2___
Only the two 1s electrons are core electrons.

Ca
Valence =
2___
The electron configuration of calcium is [Ar] 4s2. It contains no
unfilled sublevels, so only the outermost s electrons are valence
electrons. Thus, calcium has two valence electrons, the two 4s electrons.
Alternatively, calcium is a 2A metal, so it contains two valence electrons.

Core =
18___
The electron configuration of calcium is [Ar] 4s2.
The argon core, [Ar], is composed of the core electrons in calcium. Argon contains
18 electrons, so calcium contains 18 core electrons. Note that the valence
electrons are often all of those after the noble gas core, but not always.

Sn
Valence =
4___
The electron configuration of tin is [Kr] 5s2 4d10 5p2.
The 5p sublevel is unfilled, so the 5p and 5s sublevels contain the
valence electrons. Thus, tin has four valence electrons. Alternatively,
tin is a 4A metal, so it must contain four valence electrons.

Core =
46___
The core electrons come from the filled 4d sublevel and the krypton core, so
there are 46 (10 + 36) core electrons in Sn. This is an example of an atom
whose valence electrons are not all of those beyond the noble gas core.

3.1-7. Main Group Valence Configurations Exercise
Exercise 3.2:
Write the valence electron configuration of each of the following main
group elements.(Separate all terms by a single space and indicate all superscripts with a carat (^). For example, 2s^2 2p^2 for 2s2 2p2.)
Si (Z = 14)
o_3s^2 3p^2_s
Silicon is a Group 4A element, so it has four valence electrons. It is
in the third period, so its valence electron configuration is
3s2 3p2.

K (Z = 19)
o_4s^1_s
Potassium is a Group 1A element, so it has only one valence electron.
It is in the fourth period, so its valence electron configuration is
4s1.

Tl (Z = 81)
o_6s^2 6p^1_s
Thallium is a Group 3A element, so it has three valence electrons. It is
in the sixth period, so its valence electron configuration is
6s2 6p1. Note that the 5d and 4f sublevels are full,
so those electrons are not valence electrons.

Br (Z = 35)
o_4s^2 4p^5_s
Bromine is a Group 7A element, so it has seven valence electrons. It is
in the fourth period, so its valence electron configuration is
4s2 4p5.

3.1-8. Transition Metal Valence Configurations Exercise
Exercise 3.3:
Write the valence electron configuration for each of the following
transition elements.(Separate all terms by a single space and indicate all superscripts with a carat (^). For example, 2s^2 2p^2 for 2s2 2p2.)
Ti
o_4s^2 3d^2_s
Titanium is the second member of the d block, so its valence electron
configuration is 4s2 3d2.

Fe
o_4s^2 3d^6_s
Iron is the sixth member of the d block, so its valence electron
configuration is 4s2 3d6.

Cu
o_4s^1 3d^10_s
Copper is the ninth member of the d block, but it is one of the two
exceptions. Its valence electron configuration is 4s1 3d10.

3.1-9. More Valence Electron Configuration Exercises
Exercise 3.4:
Use the periodic table to help you write valence electron configurations for the following atoms. (Separate all terms by a single space and indicate all superscripts with a carat (^). For example, 2s^2 2p^2 for 2s2 2p2.)

Sc
o_4s^2 3d^1_s
The valence electron configuration of scandium is 4s2 3d1.

N
o_2s^2 2p^3_s
The valence electron configuration of nitrogen is 2s2 2p3.

Co
o_4s^2 3d^7_s
The valence electron configuration of cobalt is 4s2 3d7.

Bi
o_6s^2 6p^3_s
The 4f and 5d blocks are filled, so they are not valence electrons. The valence electron configuration of bismuth is 6s2 6p3. Note the configuration shows five valence electrons, consistent with the fact that bismuth is in Group 5A.

Sr
o_5s^2_s
Strontium is 5s2.

Mn
o_4s^2 3d^5_s
Manganese is 4s2 3d5.

3.2 Shielding and Effective Nuclear Charge
Introduction
In this section, you will learn how to predict the relative strengths with which the valence electrons interact with the nucleus.3.2-1. Effective Nuclear Charge Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
3.2-2. Shielding and Effective Nuclear Charge
Core electrons shield valence electrons better than do other valence electrons.

Figure 3.1a
In the absence of any electrons, the full nuclear charge (as shown by the red color) is observed. The nuclear charge is +Z, where Z is the atomic number (the number of protons in the nucleus). If this were a calcium nucleus, the resulting charge would be +20.
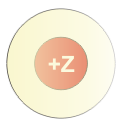
Figure 3.1b
The nuclear charge is shielded by the negative charge of the core electrons (yellow sphere). Thus, only a portion of the nuclear charge can be felt through the core electrons as shown by the fact that the red color is greatly reduced by the yellow sphere. If this were a Group 2A element, the charge that would result would be +2 as the two valence electrons are not included. Thus, the
charge has been reduced from +40 to +2 by the core electrons.

Figure 3.1c
Addition of the valence electrons (green sphere) results in the atom. Essentially none of the nuclear charge is felt outside the neutral atom.
3.2-3. Trends in Zeff
Effective nuclear charge increases going from left to right in a period.
-
1Z = 3for Li, which is 1s22s1. Zeff ~ 1 according to Figure 3.2. Thus, the two 1s electrons exert a shielding ofσ ~ 3 − 1 = 2.
-
2Z = 9for F, which is 1s22s22p5, but Zeff ~ 5. Thus, the shielding is σ ~ 9 – 5 = 4.
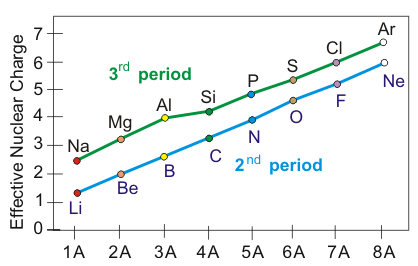
Figure 3.2
Effective Nuclear Charges of the Elements in the 2nd and 3rd Periods
n = 2
electrons do not shield as well as the n = 1
electrons.
This effect opposes that of changing the n quantum number because increasing n increases the energy of the valence levels, but increasing the effective nuclear charge lowers the energy of the valence levels. The effect of increasing n is the more important because the energies of the valence levels do increase going down a group.
3.2-4. Effective Nuclear Charge Exercise
Exercise 3.5:




Select the electron in each pair that experiences the greater effective nuclear charge.
-
2p in Cl
-
2p in F The Cl nucleus has eight more protons and eight more electrons, but most of the additional electrons are in then = 3level, so they do not shield the 2p very will. Thus, the 2p in Cl experiences a higher nuclear charge than do the 2p in F.

-
3p in Cl
-
3p in P Effective nuclear charge increases going across a period.

-
4p in Br The p orbitals have a nodal plane at the nucleus, but s orbitals do not. Thus, s orbitals screen the p orbitals better than the p orbitals screen the s.
-
4s in Br

-
5s in Rb
-
4s in K Effective nuclear charge experienced by the valence electrons increases slightly going down a group.

3.3 Relative Atomic Size
Introduction
Atoms are not hard spheres with well defined boundaries, so the term "atomic radius" is somewhat vague and there are several definitions of what the atomic radius is. Consequently, atomic radii are not measured directly. Rather, they are inferred from the distances between atoms in molecules, which can be readily determined with several techniques. However, a discussion of how atomic radii are defined requires an understanding of chemical bonding and the solid state, so a detailed discussion of the different types of radii and their values is postponed until Chapter 8. In this section, we restrict our discussion to trends in the relative sizes of atoms.Prerequisites
-
•1.8 Electromagnetism and Coulomb's Law
-
•1.11 Dimitri Mendeleev and The Periodic Law
-
•2.3 Bohr Model (Use the Bohr model to relate the size of an orbital to its n quantum number and atomic number.)
Objectives
-
•Explain the periodicity in the size of valence orbitals.
-
•Determine the relative sizes of atoms based on their positions in the periodic table.
3.3-1. The Bohr Model and Atomic Size
The size of the atom is given by the size of its valence electron clouds. Although the orbits of fixed radii suggested in the Bohr model are not correct, the conclusions of the model can still be used to gain a qualitative understanding of trends in atomic radii by substituting the effective nuclear charge for the atomic number in Equation 2.4 to obtain the following:-
•The average size of an orbital increases as its n quantum number increases.
-
•The size of the electron cloud decreases as the effective nuclear charge it experiences increases.
3.3-2. Atomic Size
Atomic radii increase going down a group and decrease going across a period.
-
•atomic radii increase going down a group because the n quantum number of the outermost orbitals increases, and
-
•atomic radii decrease going from left to right in a period because Zeff increases.
0.37 Å
and 2.11 Å,
respectively.
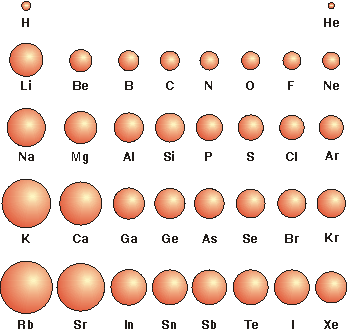
Figure 3.3
Relative Atomic Radii
3.3-3. Atomic Size Exercise
Exercise 3.6:



-
Cl Atomic radii increase going down a group.
-
F Atomic radii increase going down a group.
-
I

-
Na
-
S Atomic radii decrease going across a period.
-
Al Atomic radii decrease going across a period.

-
Br Atomic radii decrease going across a period.
-
K
-
Ge Atomic radii decrease going across a period.

3.4 Relative Orbital Energies
Introduction
The relative energy of the valence orbitals in an atom is an important characteristic of the atom as it dictates both properties of the atom and the manner and strength of its interaction with other atoms. Indeed, we will invoke relative orbital energies in making predictions about chemical processes throughout the remainder of this course. In this section, we use the Bohr model to predict the relative energies of the valence orbitals in some small atoms.Prerequisites
-
•1.8 Electromagnetism and Coulomb's Law
-
•1.11 Dimitri Mendeleev and The Periodic Law
-
•2.3 Bohr Model (Use the Bohr model to relate the energy of an orbital to its n quantum number and atomic number.)
Objectives
-
•Determine the relative energies of electrons based on their n quantum number and the effective nuclear charge they experience.
3.4-1. Orbital Energies Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
3.4-2. The Bohr Model and Orbital/Electron Energy
The ease with which an electron is lost from an atom is given by how strongly the electron is bound to the atom, which, in turn, is given by the energy of the electron in the atom. We again use the conclusions of the Bohr model in a qualitative way to understand trends in valence electron energies by substituting the effective nuclear charge for the atomic number in Equation 2.5 to obtain Equation 3.2. Ex is the energy of a valence orbital on atom X, and n is the principle quantum number of its valence shell. While Equation 3.2 is only a very rough approximation, it is useful in demonstrating how the relative orbital energies of the valence electrons in the atoms of the first three periods are related. We conclude that-
1The energy of an electron increases (becomes less negative and is bound less tightly) as its n quantum number increases.
-
2The energy of an electron decreases (becomes more negative and is bound more tightly) as the effective nuclear charge increases.
3.4-3. Relative Energies, an Example
The valence orbitals of nonmetals are relatively low in energy, while those of metals are relatively high.
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
Ex ∝ −
and the values in the table to conclude the following.
| Zeff2 |
| n2 |
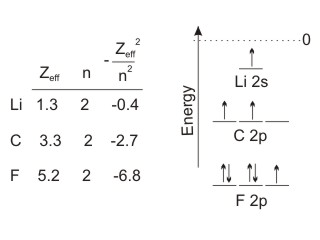
Figure 3.4
-
•The five 2p valence electrons of fluorine experience a highly positive effective nuclear charge of 5.2 and a very low n quantum number, so the value foris quite large. Thus, the energy of the valence orbitals of fluorine is very low. Indeed, they are the lowest-energy valence orbitals of any atom. Nonmetals are all characterized by low-energy valence orbitals.
Zeff2 n2 -
•The two 2p electrons of carbon experience an effective nuclear charge of +3.3 and the same n quantum number as fluorine, so the value ofis less than that of fluorine. Thus, the valence electrons of carbon are not bound as tightly as those on fluorine and the carbon valence orbitals are higher in energy than those of fluorine. However, carbon is a nonmetal, and the energy of its valence orbitals is still relatively low.
Zeff2 n2 -
•Lithium is a metal, and its 2s valence electron experiences an effective nuclear charge of only +1.3, which produces a very low value for Zeff squared over n squared. Consequently, the valence electron on a lithium atom is bound only weakly, and its valence orbital energy is quite high. Indeed, metals are all characterized by high-energy valence orbitals.
3.4-4. Predicting Relative Energy Exercise
Exercise 3.7:




Use the effective nuclear charges (Figure 3.2) and the n quantum number of the valence electrons of chlorine, oxygen, sulfur, and silicon in Equation 3.2
to those for Li (0.4), C (2.7), and F (6.8).
Ex ∝ −
to predict the relative energies of their valence orbitals. Compare to the values of | Zeff2 |
| n2 |
| Zeff2 |
| n2 |
-
Chlorine (Zeff = 6.1)
-
above Liwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place Cl above F.
=Zeff2 n2
= 4.1,6.12 32
Li - - - - - - -
-
between Li and Cwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place Cl above F.
=Zeff2 n2
= 4.1,6.12 32
C - - - - - - -
-
between C and F
F - - - - - - -
-
below Fwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place Cl above F.
=Zeff2 n2
= 4.1,6.12 32

-
Oxygen (Zeff = 4.6)
-
above Liwhich places it between F and C. Note that the valence orbitals of oxygen are lower than those of chlorine.
=Zeff2 n2
= 5.3,4.62 32
Li - - - - - - -
-
between Li and Cwhich places it between F and C. Note that the valence orbitals of oxygen are lower than those of chlorine.
=Zeff2 n2
= 5.3,4.62 32
C - - - - - - -
-
between C and F
F - - - - - - -
-
below Fwhich places it between F and C. Note that the valence orbitals of oxygen are lower than those of chlorine.
=Zeff2 n2
= 5.3,4.62 32

-
Sulfur (Zeff = 5.5)
-
above Liwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place S above O.
=Zeff2 n2
= 3.4,5.52 32
Li - - - - - - -
-
between Li and Cwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place S above O.
=Zeff2 n2
= 3.4,5.52 32
C - - - - - - -
-
between C and F
F - - - - - - -
-
below Fwhich places it between F and C. As expected, the n quantum number dominates the trends in a group to place S above O.
=Zeff2 n2
= 3.4,5.52 32

-
Silicon (Zeff = 4.3)
-
above Liwhich places it between C and Li. Note that this is also above C as expected for two elements in the same group.
=Zeff2 n2
= 2.1,4.32 32
Li - - - - - - -
-
between Li and C
C - - - - - - -
-
between C and Fwhich places it between C and Li. Note that this is also above C as expected for two elements in the same group.
=Zeff2 n2
= 2.1,4.32 32
F - - - - - - -
-
below Fwhich places it between C and Li. Note that this is also above C as expected for two elements in the same group.
=Zeff2 n2
= 2.1,4.32 32

3.4-5. Relative Valence Orbital Energies for Several Atoms
Before leaving our discussion of relative orbital energies, we add H (Zeff = 1) and O (Zeff = 4.5) to our energy diagram to obtain the following diagram that contains eight elements of the first three periods.
Figure 3.5
The relative energies of the valence orbitals of some atoms studied in the first three periods. Values of
−
are given to the right.
| Zeff2 |
| n2 |
-
1Orbital energies decrease (become more negative) going across a period because Zeff increases. Thus,Li > C > O > F.
-
2Orbital energies increase (become less negative) going down a group because n increases. Thus,Si > C;S > O;andCl > F.
3.4-6. Orbital Energy Exercise
Exercise 3.8:


Consider the following valence orbital energy diagram that we have constructed to this point.
Where would the valence orbitals of the following atoms be placed? Give the letter of the location.
| a |
| Li (–0.4) |
| b |
| H (–1.0) |
| c |
| Si (–2.0) |
| d |
| C (–2.5) |
| e |
| S (–3.3) |
| f |
| Cl (–4.2) |
| g |
| O (–5.0) |
| h |
| F (–6.5) |
-
(a) N (Zeff = 3.83)
-
a−Zeff2/n2 = −3.7
-
b−Zeff2/n2 = −3.7
-
c−Zeff2/n2 = −3.7
-
d−Zeff2/n2 = −3.7
-
e−Zeff2/n2 = −3.7
-
f
-
g−Zeff2/n2 = −3.7
-
h−Zeff2/n2 = −3.7

-
(b) P (Zeff = 4.89)
-
a−Zeff2/n2 = −2.7
-
b−Zeff2/n2 = −2.7
-
c−Zeff2/n2 = −2.7
-
d−Zeff2/n2 = −2.7
-
e
-
f−Zeff2/n2 = −2.7
-
g−Zeff2/n2 = −2.7
-
h−Zeff2/n2 = −2.7

3.4-7. Core vs. Valence Orbital Energies Exercise
The energies of the valence orbitals of all atoms lie in a relatively narrow range due to the periodicity in Zeff and an increasing n quantum number. Core electrons, on the other hand, continue to drop in energy as the number of protons increases because they are not shielded very efficiently by the valence electrons. Thus, the valence 2p orbitals of oxygen are at lower energy than the valence 3p valence orbitals on sulfur because valence orbital energies increase going down a group, but the 2p electrons in oxygen are much higher in energy than the 2p electrons on sulfur because sulfur has 16 protons while oxygen has only eight.
Exercise 3.9:



Select the orbital that is at lower energy in each pair.
-
2p on N The orbitals are on the same atom, so usen + l,which is 3 for a 2p and 2 for a 2s.
-
2s on N

-
2p on Br
-
2p on Fn = 2for both orbitals, but Zeff is much greater in the vicinity of the 35 protons of a Br atom than around the nine protons of a F atom. The 2p electrons in Br are core electrons, while those in F are valence electrons, and core electrons are always lower in energy than valence electrons.

-
2p on N Zeff increases going across a period, while n remains the same.
-
2p on O

3.5 Ionization Energy
Introduction
One of the properties of an atom that is important in dictating the chemical properties of the atom is the ease with which the atom loses one or more of its valence electrons. This property of an atom is given by the atom's ionization energy or ionization potential, the topic of this section.Prerequisites
-
•1.8 Electromagnetism and Coulomb's Law
-
•1.11 Dimitri Mendeleev and The Periodic Law
-
•2.3 Bohr Model (Use the Bohr model to relate the energy of an orbital to its n quantum number and atomic number.)
Objectives
-
•Predict the relative ionization energies of atoms based on their positions in the periodic table or the relative energies of their occupied valence orbitals.
3.5-1. Ionization Energy Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
3.5-2. Ionization Energy and Orbital Energy
Ionization energies measure the energy of the highest energy electron.
| M | → | M1+ + e1− | First ionization | |
| M1+ | → | M2+ + e1− | Second ionization | |
| M2+ | → | M3+ + e1− | Third ionization | |
| M3+ | → | M4+ + e1− | Fourth ionization |
3.5-3. Putting Numbers to Orbital Energies
The energy required to remove one 2p electron from each atom in a mole of F atoms to produce a mole of F1+ ions is 1681 kJ, so the ionization energy of fluorine is 1681 kJ/mol. In addition, 1681 kJ/mole are released in the reverse process, so we conclude that the 2p orbital energy is –1681 kJ/mol. Nonmetals are characterized by high ionization energies and low valence orbital energies because they have high effective nuclear charges. The ionization energy of carbon is 1086 kJ/mol, so the orbital energy of a 2p orbital in carbon is –1086 kJ/mol. The ionization energy of lithium is only 520 kJ/mol, so the orbital energy of its 2s orbital is –520 kJ/mol. The valence orbitals of metals are characterized by low ionization energies and high valence orbital energies because they have low effective nuclear charges.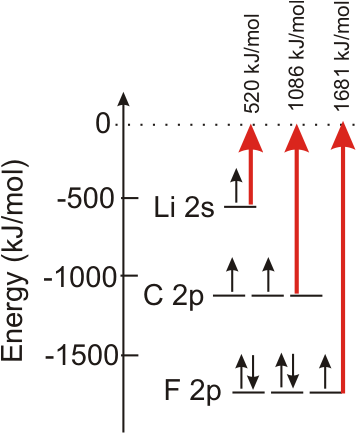
Figure 3.6
Ionization Energy and Orbital Energy
3.5-4. Ionization Energy Trends
Ionization energies increase going up a group and going from left to right in a period.
Ex ∝ −
, so we conclude that ionization energies
| Zeff2 |
| n2 |
-
•increase moving up a group due to the decrease in the n quantum number, and
-
•increase from left to right in a period due to the increase in Zeff.

Figure 3.7
First Ionization Energies of the Main Group Elements: Circles of the same color represent elements of the same group. For example, all Group 1A elements are shown as red circles.
-
•Metals are characterized by low effective nuclear charge, so they all have low ionization energies. Consequently, metals tend to lose electrons, and the farther to the left of the Periodic Table, the more easily the electrons are lost. Thus, the 1A elements lose their valence electron very easily. The ionization energy also decreases going down a family, so Cs (high n and low Zeff) loses its valence electron so easily that it must be stored in oil because it gives up its 6s electron to water or oxygen when exposed to the air.
-
•Nonmetals have high effective nuclear charges, so they have relatively high ionization energies. Thus, nonmetals do not lose their electrons very easily. Excluding the noble gases, F (low n and high Zeff) has the highest ionization energy of any atom, which means that the valence electrons of fluorine are very tightly bound.
3.5-5. Ionization Energy Exercise
Exercise 3.10:




-
Cl Ionization energies increase going up a group.
-
F
-
I Ionization energies increase going up a group.

-
Na Ionization energies increase going across a period.
-
S
-
Al Ionization energies increase going across a period.

-
Br
-
K Ionization energies increase going across a period.
-
Ge Ionization energies increase going across a period.

-
Si Half-filled sublevels are unusually stable.
-
P
-
S Half-filled sublevels are unusually stable.

3.6 Electronegativity
Introduction
The electrons in a bond can lower their potential energy by residing closer to the atom in the bond that has the valence orbital at lower energy. The ability of an atom to attract the bonding electrons to itself is called its electronegativity (χ). Atoms are most electronegative when their valence orbitals are low in energy. Electronegativity is the topic of this section.Prerequisites
-
•1.8 Electromagnetism and Coulomb's Law
-
•1.11 Dimitri Mendeleev and The Periodic Law
-
•2.3 Bohr Model (Use the Bohr model to relate the energy of an orbital to its n quantum number and atomic number.)
Objectives
-
•Predict the relative electronegativities of atoms based on their positions in the periodic table or the relative energies of their unfilled valence orbitals.
-
•Explain the differences between metals and nonmetals that arise from the differences in their ionization energies and electronegativities.
3.6-1. Electronegativity Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
3.6-2. Electronegativity and Orbital Energy
Atoms with low-energy valence orbitals are highly electronegative.
Example:
En = −
,
so the valence orbitals of atoms with high electronegativities have
| (Zeff)2 |
| n2 |
-
1large Zeff (nonmetals) and
-
2low n quantum numbers (high in the periodic table).
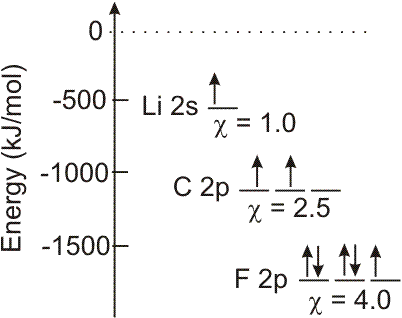
Figure 3.8
Electronegativity and Orbital Energy
3.6-3. The Meaning of Electronegativity
The electronegativity difference between two atoms dictates the type of bond that forms between them. Refer to Figure 3.9 for the following discussion.-
1The electronegativities of two fluorine atoms are identical, so the bonding electrons are shared equally by the two atoms. Bonds in which the bonding electrons are shared equally are called covalent bonds.
-
2Fluorine is more electronegative than carbon, so the bonding electrons in a C-F bond reside closer to the fluorine atom. The excess of electron density close to the fluorine atom gives it a partial negative charge. A Greek delta (δ) is used to indicate that it is only a partial charge as the carbon still experiences some of the negative charge of the bonding electrons.
-
3The electronegativity difference between Li and F is so great that the bonding electrons reside almost exclusively on the fluorine to give it a full negative charge. Bonds in which the bonding electrons are not shared but reside on one atom are called ionic bonds.
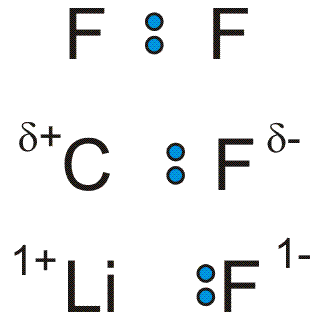
Figure 3.9
3.6-4. Electronegativity Trends
Electronegativities decrease going down a group and increase going across a period.
-
•electronegativities decrease going down a group because n increases, which causes the orbital energies to increase, and
-
•electronegativities increase going from left to right in a period because Zeff increases, which causes the orbital energies to decrease (become more negative).
-
•Nonmetals are characterized by high Zeff, so their valence orbitals are low in energy. Consequently, nonmetals are highly electronegative (2.0 to 4.0).
-
•Main group metals have low effective nuclear charges and are characterized by high energy valence orbitals. Thus, main group metals have very low electronegativities (0.7 to 1.5).
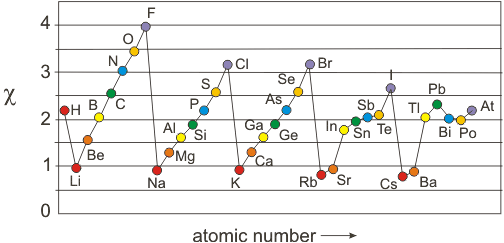
Figure 3.10
Electronegativities of the Main Group Elements: Circles of the same color represent elements of the same group. For example, all Group 1A elements are shown as red circles.
3.6-5. Late Metals
An exception to the above generality about the electronegativities of metals arises from the fact that d and f electrons do not shield very well because they contain two and three nodal planes, respectively. Therefore, the effective nuclear charge experienced by the valence orbitals in late metals (metals that lie on the right side of the Periodic Table) can be quite large. For example, Pb has 27 more protons and electrons than does Cs, but 24 of those electrons are d and f electrons, which do not shield the 27 additional protons very well. Thus, the 6p electrons in Tl and Pb experience relatively high Zeff (12.25 and 12.39, respectively), which makes both of these metals fairly electronegative. Indeed, the electronegativity of Pb is much greater than that of Si even though they are in the same Group, and the valence orbitals in Pb have a much higher n quantum number. We conclude that due to their high effective nuclear charges, late metals have unusually high electronegativities (see Table 3.2), which impacts significantly on their chemical properties.| Metal | χ |
|---|---|
| Ag | 1.9 |
| Sn | 2.0 |
| Hg | 2.0 |
| Tl | 2.0 |
| Pb | 2.3 |
Table 3.2: Electronegativities of Late Metals
3.6-6. Metals vs. Nonmetals
Metals have low ionization energies and nonmetals have high electronegativities.
-
•relatively large atomic radii
-
•lower ionization energies
-
•lower electronegativities
-
•relatively small atomic radii
-
•higher ionization energies
-
•higher electronegativities
3.6-7.Electronegativity Exercise
Exercise 3.11:




-
Cl Electronegativity increases going up a group.
-
F
-
I Electronegativity increases going up a group.

-
Na Electronegativity increases going across a period.
-
S
-
Al Electronegativity increases going across a period.

-
Br
-
K Electronegativity increases going across a period.
-
Ge Electronegativity increases going across a period.

-
Al Late metals have unusually high electronegativities.
-
Tl
-
Ga Late metals have unusually high electronegativities.

3.6-8. Orbital Energy and Atomic Properties Exercise
Exercise 3.12:


Use what you have learned about the relationships between orbital energies and ionization energies and
electronegativities and the valence orbital occupancies of atoms X and Y given below to answer the following questions about atoms X and Y.
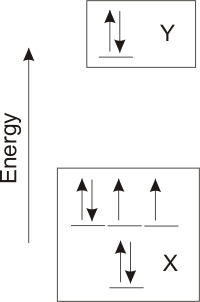

-
The atom with the lower ionization energy:
-
X Atoms with lower ionization energies have electrons at higher energy. The electrons in atom Y are higher than those in atom X, therefore, element Y has the lower ionization energy.
-
Y

-
The atom with the higher electronegativity:
-
X
-
Y Atoms with higher electronegativities have valence orbitals at lower energy. The valence orbitals of X are lower than those of Y, so atom X is much more electronegative than atom Y.

The group of the periodic table to which each atom belongs:
X
o_6A_s
Atom X has six valence electrons (ns2np4) so it is a
Group 6A element.

Y
o_2A_s
Atom Y has two valence electrons (ns2), so it is a Group 2A
element.

3.7 Magnetic Properties
Introduction
All magnetic properties are due to the magnetic fields caused by electron spin. However, no magnetic field is generated by paired electrons because the two different electron spins are opposed and their magnetic fields cancel. Consequently, the magnetic properties of an atom are due solely to its unpaired electrons. In this section, we give a brief introduction into the magnetic properties of atoms and materials.Prerequisites
-
•2.5 The Quantum Numbers (Explain the meaning of the ms quantum number.)
Objectives
-
•Explain the origin of magnetism.
-
•Distinguish between paramagnetic and diamagnetic atoms.
-
•Explain why magnetic atoms are not always magnetic materials.
3.7-1. Paramagnetism and Diamagnetism
The paramagnetism of an atom increases with the number of unpaired electrons.
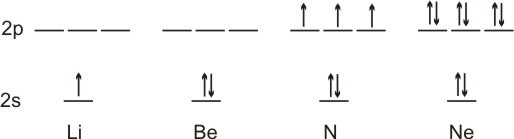
Figure 3.11
3.7-2. Ferromagnetism
Ferromagnetism is a measure of the bulk magnetism of a material, while paramagnetism is a measure of the magnetism of individual atoms.
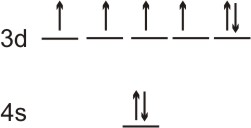
Figure 3.12
Valence orbital occupancy of Fe. It is both paramagnetic and ferromagnetic.
3.7-3. Paramagnetism Exercise
Exercise 3.13:



-
O O is 2s22p4, so it has two unpaired electrons in its 2p sublevel. N is 2s22p3, so it has three unpaired electrons.
-
N

-
Na
-
Mg Na is 3s1 and has one unpaired electron. Mg is 3s2, so it has no unpaired electrons

-
Cr
-
Fe Cr is 4s13d5 (an exception), so it has six unpaired electrons. Fe has only four unpaired electrons.

