Solution Chemistry: Making Solutions, Reactions, and Solubility
Organization
-
•Mode: laboratory, groups of 4
-
•Grading: goggles, closed-toe shoes, appropriate attire
-
•Safety: lab report, individual, due at start of next lab meeting
| CHEM 115 Expt. 8 | Chemical Classification | Possibility Of: | NFPA Codes | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Solutions and Solubility |
Poison A
|
Flammable Gas
|
Flammable Liquid
|
Combustable Liquid
|
Reacts with Water
|
Oxidizer
|
Organic Peroxide
|
Poison B
|
Corrosive Acid
|
Corrosive Base
|
Irritating or Harmful
|
Misc. Hazard
|
No Hazard
|
Fire
|
Sudden Release of Pressure
|
Reactive
|
Immediate (Acute) Health Hazard
|
Delayed (Chronic) Health Hazard
|
Fire
|
Health
|
Reactivity
|
Special Precautions
|
| Lead(II) Nitrate | X | X | X | X | 0 | 3 | 1 | OX | ||||||||||||||
| Potassium Iodide | X | X | 0 | 1 | 0 | |||||||||||||||||
| Copper(II) Sulfate | X | 1 | 2 | 1 | ||||||||||||||||||
| Sodium Hydroxide | X | X | X | 0 | 2 | 1 | COR | |||||||||||||||
I: Background
Much of what we know about the chemical behavior of the elements comes from the very careful observations of change made by chemists through the centuries. Many of these observations were made without the use of sophisticated instrumentation that has become a permanent part of working laboratories today. Most of us would not consider drawing a conclusion about a change in mass without the use of an analytical balance similar to the ones you now use in this laboratory. Yet the correct chemical formula for water, H2O, was determined without the aid of sophisticated balances, by observing and measuring the relative volume of H2(g) and O2(g) needed to produce a measured volume of water. In the lab today and next week, you will have many opportunities to observe chemical change. In today's lab, you will make solutions and mix them together to see if a reaction takes place. You will use solubility rules to predict the product of the reaction and write and balance the equation of the reaction taking place.Part A: Concentrations of Solutions
A lot of chemistry takes place in aqueous solution. Solutions consist of a solute dissolved in a solvent. The amount of solute dissolved in a solvent is the concentration of the solution. Concentrations can be expressed in many different ways. Percent by volume is used to express the concentration of rubbing alcohol, vinegar, and alcoholic beverages. A 100 mL sample of 70% rubbing alcohol solution contains 70 mL of isopropanol. A 12 oz soda typically contains 44 grams of sugar, giving a concentration of 44 grams/12 oz or 3.7 g sugar/oz beverage. One ounce is 2 tablespoons. The most convenient concentration unit for chemists is molar concentration abbreviated by M. The definition of molar concentration is moles of solute/unit volume of solution in liters. A 2.0 M solution of NaCl has 2.0 moles of NaCl dissolved in one liter of solution. Chemists find molar concentration a convenient unit system, because when we plan an experiment, we plan it for mole amounts of reactants and products. If we need 0.50 mole of NaCl for an experiment, we can calculate the volume of 2.0 M NaCl to use to deliver the 0.50 mole wanted in the experiment.Example 1: Calculation of the Amount of Solid Needed to Make a Solution
Let's take the 2.0 M solution of NaCl as an example of how calculations to make solutions are done, and let's say that you want to make 0.25 L of a 2.0 M NaCl solution. You need to figure out how much NaCl you need in order to make this solution. Because NaCl is available as a solid, the answer to "how much" will be in units of grams. The question to be solved is this.
How many moles of NaCl are needed to make 0.25 L of 2.0 M NaCl?
-
1.How many moles of NaCl are needed to make 0.5 L of 2.0 M NaCl?
-
2.How many grams of NaCl does this correspond to?
1
How many moles of NaCl are needed to make 0.25 L of 2.0 M NaCl? Let's go back to the definition of molar concentration, Eq. 1, in a slightly simpler form.
This equation relates molar concentration, M, moles, and volume of solution. Given any two of these three quantities, you can rearrange the equation to solve for the third.
Analysis—We have the volume of solution (0.25 L) and the concentration of solution (2.0 M). We need to find moles of solute (in this case NaCl). Keeping in mind that 2.0 M NaCl is defined as 2.0 moles NaCl/L solution, rearrange Eq. 1 to solve for moles NaCl.
Solve: The general setup is moles solute = (M)(V).
| Solve: | moles NaCl | = |
| ||||
| moles NaCl | = | 0.50 moles |
2
How many grams of NaCl does 0.50 mole of NaCl correspond to?
Analysis—This is a standard grams to moles conversion that uses the molar mass (molecular weight) to solve it. The definition of molar mass is the following.
The molar mass can always be calculated if the formula of the substance is known and a periodic table is handy. This equation can be rearranged as needed to solve for grams or moles given the other quantity. For this example, we know moles of NaCl and want to solve for grams.
| Solve: | rearrange Eq. 2: | grams | = | (moles)(molar mass) | ||||
| grams NaCl | = | (0.50 moles NaCl)
| ||||||
| grams NaCl | = | 29.22 grams |
When 29.22 grams are dissolved in water to a final volume of 0.25 L, the concentration of the solution will be 2.0 M.
Example 2: Calculation of the Amount of a Concentrated Solution Needed to Make a Solution of Lower Concentration
Many acids are only sold as solutions of high concentration and are not available as a solid. It is also sometimes convenient to make stock solutions of a high concentration that can be used to prepare solutions of a lower concentration. In these cases, a quantity of a solution at a high concentration can be diluted to give a solution of the desired concentration. For this example, the task is to calculate the amount of 6.0 M HCl needed to make 500 mL of 2.0 M HCl. The key point is that the moles of solute present in the final solution (500 mL of 2.0 M) must be equal to the moles of solute removed from the initial solution (6.0 M HCl). If we call the initial solution "Solution 1" and the final solution "Solution 2", we can express this requirement as follows.
moles1 = moles2 or n1 = n2
What volume of 6.0 M HCl is needed to make 500 mL of 2.0 M HCl?
| V1 | = |
| ||
| V1 | = |
|
Part B: Solubility Rules
Each of the solutions made in Part A involves dissolving an ionic solid in water. The NaOH solution provided in the lab was initially made as an ionic compound dissolved in water. Solubility rules (Appendix F: Supplemental Data) summarize the solubility of different types of ionic compounds in water. Solubility is a quantitative property of compounds and is different for different compounds. For example, the solubility of NaCl is 35.9 g/100 mL of water at 20°C, while the solubility of NaNO3 is 73 g/100 mL of water at 20°C. However, both of these sodium salts are classified according to the solubility rules as soluble by the first rule—all compounds containing group I ions are soluble. Compounds that are classified by the rules as insoluble do dissolve in water, but at very low levels. The solubility of calcium carbonate is 0.0013 g/100 mL of water at 20°C, and this is such a low level that calcium carbonate (and carbonates in general) are considered to be insoluble. The solubility rules roughly divide compounds into a soluble category if 0.10 g of the substance dissolves in 100 mL of water, and insoluble if less than 0.10 g of the substance dissolves in 100 mL of water. The Table of Solubility Rules is generally useful, and certainly easier than looking up the solubility of each salt individually.Collisions Between Ions in Solution Can Result in a Chemical Reaction that Produces an Insoluble Ionic Compound.
We can use the solubility rules to predict the identity of the solid compound that forms in the reaction between lead(II) nitrate and potassium iodide. We can predict the formulas of the possible products, and we can use the solubility rules to predict which product is the insoluble compound observed in the reaction. In solution, the ions from the reactants are all present in the beaker along with water molecules. The ions are in motion and will bounce into each other and into the water molecules. Ignoring for now the encounters with the water molecules, think about the different interactions between the ions present in the solution. Each ion could collide with any of the other ions present. When predicting the possible products between ions in solution, the only collisions to consider are those that could result in the formation of an insoluble ionic compound.What Sorts of Interactions Between Ions Can Lead to a New Substance?
Reaction 1:
Pb(NO3)2 and KI ions present: Pb2+(aq), NO3–(aq), K+(aq), I–(aq)
Pb(NO3)2 and KI ions present: Pb2+(aq), NO3–(aq), K+(aq), I–(aq)
| Collision | Potential for Chemical Reaction |
| K+(aq) and I–(aq) | No reaction—this is what we started with, we already know this isn't going to form an insoluble compound. |
| K+(aq) and Pb2+(aq) | No reaction—like charges repel and won't form an ionic compound. |
| Pb2+(aq) and I–(aq) | Possible product PbI2—the cation of one reactant with the anion of the other reactant |
Part C: Writing and Balancing Chemical Equations
To write the equation of the reaction that takes place, use the formulas of the reactants. If the reactants are soluble in water, use (aq) as the physical state. Write the formulas of the products on the product side, indicating their solubility with (aq) for water-soluble compounds and (s) for insoluble compounds (solid).
Pb(NO3)2(aq) + KI(aq) → PbI2(s) + KNO3(aq)
Balance the equation. The easiest way to balance equations for ionic compounds is to balance by ions instead of balancing by atoms. Rather than balancing nitrogen and oxygen separately, balance nitrate ions on both sides of the equation. On the left, there are two nitrates in Pb(NO3)2, but on the right, there is only one nitrate in KNO3. To match the stoichiometry of the reactant, the coefficient of the product, KNO3, needs to be changed to a 2.
Pb(NO3)2(aq) + KI(aq) → PbI2(s) + 2 KNO3(aq)
Now there are two potassium ions in 2 KNO3 on the right, but still only one on the left. This means the stoichiometric coefficient of KI on the left also needs to be changed to 2.
Pb(NO3)2(aq) + 2 KI(aq) → PbI2(s) + 2 KNO3(aq)
The potassium ions and nitrate ions are now balanced. Check the lead(II) ion (one on each side) and the iodide ions (two on each side), to make sure that the entire equation is balanced.
Summary: How to Predict the Products of a Reaction Between Ions in Solution
-
1.Identify the ions present—K+(aq), I–(aq), Pb2+(aq), and NO3–(aq).
-
2.Write the formulas for the potential products—KNO3 and PbI2.
-
3.Use solubility rules to predict the physical states (states of matter) of products that are ionic compounds.
Part D: Physical Models of Ions in Solution
The model that best depicts the behavior of a soluble ionic compound in solution has cations and anions separated from each other and dispersed throughout the solution. In a solid, however, the cations and anions form an ionic bond, and so are depicted in contact with each other in a well-ordered array on the bottom of the beaker. The models in Figure 1 represent one way in which chemists think of the behavior of ionic compounds in solution. But it's cumbersome to always draw a picture of what's happening, so chemical equations are used to depict what happens when ionic compounds (including acids) are put in solution. This is the purpose of writing complete ionic equations and net ionic equations—to describe the behavior of the dominant forms of ionic compounds in solution in terms of their chemical formulas (the complete ionic equation), and to highlight the interaction between ionic species that leads to the formation of a new product (the net ionic equation). Shown in Figure 1 are several models that depict the behavior of compounds in water at the particle level.
Figure 1: Physical Models of Compounds in Water
How Do We Depict the True Behavior of Ionic Compounds in Solution Using Formulas and Equations?
Using the letter M to denote the cation and the letter X to denote the anion, the chemical equation that describes the dissolution of a soluble ionic compound in water is as follows.| Case 1: | |
| MnXm(s) → Mm+(aq) + Xn−(aq) |
| Examples: | |
| NaCl(s) → Na+(aq) + Cl−(aq) | |
| K2SO4(s) → 2 K+(aq) + SO42−(aq) |
| Case 2: | |
| Mm+(aq) + Xn−(aq) → MnXm(s) |
| Example: | |
| Cu2+(aq) + 2 OH−(aq) → Cu(OH)2(s) |
From Chemical Equations to Complete Ionic and Net Ionic Equations
The chemical equation provides an overview of all of the reactants and products involved in a chemical reaction, but it doesn't really drill down to what's happening when the reactants are placed in water, or which species are responsible for the formation of the product. To communicate that level of detail, complete (full) ionic and net ionic equations are used. Model 1: Writing the Complete Ionic Equation In this lab, you will carry out the reaction—Pb(NO3)2(aq) + 2 KI(aq) → PbI2(s) + 2 KNO3(aq). To write the complete ionic equation, the soluble ionic compounds are written as dissociated ions (the dominant form of the compound when placed in water), while insoluble ionic compounds are written as the solid (the dominant form of the compound when placed in water). The stoichiometry of the compound formula must be reflected, as well as the stoichiometry of the chemical equation. Example for Pb(NO3)2-
a.Write the ions present in the compounds as Pb2+(aq) + 2 NO3–(aq), and K+(aq) + I–(aq), respectively.
-
b.Multiply K+(aq) + I–(aq) by the stoichiometric coefficients determined from Pb2+(aq) and 2 NO3–(aq).
II: Exercises
Part A: Making Solutions of a Desired Concentration
You will work in groups of 4 to make solutions and run reactions involving those solutions. Assign one of the solutions below to each student in the group. Read through Example 1 and Example 2 in the backround section carefully to learn how to perform the calculations.| Solutions | Reactant | Available State | Volume to Make | Concentration |
|---|---|---|---|---|
| 1 | Pb(NO3)2 | solid | 50.0 mL | 0.100 M |
| 2 | KI | solid | 50.0 mL | 0.100 M |
| 3 | CuSO4 · 5 H2O | solid | 50.0 mL | 0.100 M |
| 4 | NaOH | 0.500 M NaOH | 50.0 mL | 0.100 M |
Do Your Calculations
In your notebook, calculate the amount of reactant you need in order to make the solution assigned to you (see Table 1). The formulas given in Table 1 must be used to calculate the molar masses for the reactants available as the solid—include the 5 water molecules when calculating the molar mass of the copper(II) sulfate compound.Make Your Solution
There are many types of glassware used in a chemistry lab, and they all have a different purpose. Beakers are convenient containers for solutions and reactions, but they are not used for accurate measurements of volumes. Even though there are volume markers on the side of the beaker, the error in the volume measured is +/- 5 mL. The errors associated with volume measurement using a graduated cylinder are much smaller, typically tenths of a mL, while volumetric flasks and pipets have an error of only hundredths of a mL (see below).| Glassware | Error | Error for a 50 mL Volume Measurement |
|---|---|---|
| 50 mL Beaker | 5 mL | Volume will be between 45 and 55 mL. |
| 50.0 mL Graduated Cylinder | 0.5 mL | Volume will be between 49.5 and 50.5 mL. |
| 50.00 mL Volumetric Flask | 0.05 mL | Volume will be between 49.95 and 50.05 mL. |
Making a Solution From a Solid
You will need to do the the following—weigh the boat or glassine paper, the metal, the spatula, the 100 mL beaker, the 50 mL graduated cylinder (glass), the glass stir rod, the squeeze bottle of distilled water, the tape and pen, the two 50 mL beakers, and the plastic pipet. Make sure all glassware is clean before you begin.1
Get a clean and dry plastic weigh boat or a clean piece of glassine paper. If using the glassine paper, fold it along each diagonal, so that it does not lie flat and will be better able to contain the solid.
2
Put the weigh boat or paper on the balance. Press the tare button to zero the weight on the balance.
3
Using a metal spatula, weigh out the amount of solid calculated for the solution within 0.01 grams. Write down the actual weight of the solid in your notebook.
4
Back at your bench, put the solid in a 100-mL beaker, and add about 25 mL of water to the beaker. Use the squeeze bottle to rinse all solid out of the weigh boat or off of the glassine paper. Label the beaker with the concentration and formula or name of the compound.
5
Gently stir the solid in the water with the stir rod until it is dissolved.
6
Pour the solution into the 50 mL graduated cylinder. Use the squeeze bottle to rinse all solution out of the beaker and into the graduated cylinder.
7
Add distilled water up to about the 48 mL mark on the graduated cylinder. The volume of solution in the cylinder is read at the bottom of the curved meniscus of solution (see example in Figure 2).
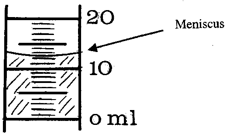
Figure 2
Use the plastic pipet to add the last few mL of water to the cylinder until the volume is 50.0 mL. If you overshoot, don't remove the extra solution. Just make a note of the fact in your notebook and see if you can estimate (and record) the final volume.
8
Pour the solution back into the labeled 100-mL beaker (drain as completely as you can, but do not rinse—addition of any more water will dilute the solution). Stir gently with the stir rod.
9
Clean the rest of the glassware. Discard any waste in the hazardous waste container.
Making a Solution: Dilutions
You will need the following—a 50 mL beaker, a 10 mL graduated cylinder, a 50 mL graduated cylinder (glass), a 100 mL beaker, a glass stir rod, a squeeze bottle of distilled water, tape, and a pen.1
Take an aliquot of the concentrated solution to your bench in a labeled 50 mL beaker. Take only a few mL more than you calculated you would need for the solution.
2
Measure the calculated amount of solution using the smaller graduated cylinder. The volume of solution in the cylinder is read at the bottom of the curved meniscus of solution (see example in Figure 2). When you are about 1 mL from the calculated volume, use a clean plastic pipet to add the last of the solution and reach the final volume.
3
Pour the solution into the 50 mL graduated cylinder. Use the squeeze bottle of distilled water to rinse the contents of the 10 mL cylinder into the 50 mL cylinder.
4
Add distilled water up to about the 48 mL mark on the graduated cylinder. Use the plastic pipet to add the last few mL of water to the cylinder until the volume is 50.0 mL. If you overshoot, don't remove the extra solution. Just make a note of the fact in your notebook, and see if you can estimate (and record) the final volume. Gently stir the solution with the stir rod.
5
Label a 100 mL beaker with the concentration and formula or name of the compound. Pour the solution into this container (drain as completely as you can, but do not rinse—addition of any more water will dilute the solution).
6
Clean the rest of the glassware. Discard any waste in the hazardous waste container.
Part B: Investigating the Reaction Chemistry of the Solutions
You will need a 50 mL beaker, a 10 mL graduated cylinder, tape, a pen, and the solutions made in Part A. Each student will carry out one of 4 different reactions, but all students will report the results of each reaction.1
Assign one of the four reactions to each student. You may decide this among yourselves.
| Reaction 1: | Pb(NO3)2 and KI |
| Reaction 2: | CuSO4 and NaOH |
| Reaction 3: | Pb(NO3)2 and CuSO4 |
| Reaction 4: | KI and NaOH |
2
Each student should label their 10 mL graduated cylinder with the formula of the solution they made. Only that solution should be put in the labeled graduated cylinder.
3
Any one assigned reaction is carried out by adding 10 mL of each of the two needed solutions into a 50 mL beaker. The 10 mL graduated cylinder is to be used to measure each solution, which is then poured into the beaker. The beaker should be labelled with the reactants being combined because all students in the group will be observing the result of the reactions.
4
In your notebook, write down all observations, including the appearance of each solution before the reaction, the appearance of the solution after the reaction, and the appearance of the solution a few minutes after the reaction. Be specific in your descriptions—color, clarity, and texture are all important observations to make.
1
Get one large beaker to collect waste from the smaller beakers and graduated cylinders. Use the squeeze bottle of water to rinse all residual solid and solution into the waste beaker, in order to minimize the amount of lead ion that is washed down the sink when the glassware is washed.
2
Pour the beaker of waste into the waste bottle using a funnel in the neck of the bottle. Rinse the waste beaker into the waste bottle with the squeeze bottle.
Caution:
If the waste bottle is full, check to see if there is an empty bottle available. If not, let the instructor know and keep the waste at the bench until a bottle is available.
If the waste bottle is full, check to see if there is an empty bottle available. If not, let the instructor know and keep the waste at the bench until a bottle is available.
3
Wash all beakers, graduated cylinders, stir rods, and other equipment. Be careful when washing glassware. Put everything away.
Part C: Analysis of the Reaction Chemistry
Based on the reactions carried out in Part B, you will now write a complete description, in the form of a balanced chemical equation, of the reactions that took place. To do this, you must learn how to predict the possible products of the reaction based on an understanding of the types of ions present in the solution, how those ions interact with each other, and the solubility rules. Then you must write and balance the chemical equation of the reaction.Predicting the Products of Reactions between Ions in Solution
-
1.Look at the solubility rules (Appendix F: Supplemental Data) and identify the rule or rules that apply in order to predict the solubility of Pb(NO3)2, KI, CuSO4, and NaOH.
-
2.Write the formulas of the ions present, with their charges, as each of these solids dissolves in water. Indicate the physical state of the ion in solution with (aq).
-
3.In the reaction between lead(II) nitrate and potassium iodide, did a chemical reaction occur? What was the evidence of a reaction occuring?
-
4.Use the solubility rules to predict the solubility of potassium nitrate and lead(II) iodide. Which rules did you use?
Writing the Balanced Chemical Equation for the Reaction that Takes Place
-
5.Write the balanced chemical equation for the reaction that took place between copper(II) sulfate and sodium hydroxide. Write the names of the products that were formed.
-
6.From the balanced chemical equation for the reaction between copper(II) sulfate and sodium hydroxide, write the balanced complete ionic equation, including physical states.
-
7.Write the net ionic equation for the reaction between copper(II) sulfate and sodium hydroxide. Identify the spectator ions.
Part D: Relating Chemical Equations to What is in the Beaker
Both lead(II) nitrate and potassium iodide are soluble ionic compounds. On your own, assign a model from Figure 1 that accurately depicts each of the following conditions.-
(a)potassium iodide in water
-
(b)lead(II) nitrate in water
-
(c)potassium nitrate in water
-
(d)lead(II) iodide in water


