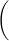Lab 6 - Rotational Equilibrium

Introduction

Have you ever tried to pull a stubborn nail out of a board or develop your forearm muscles by lifting weights? Both these activities involve using a "lever-type" action to produce a turning effect or torque through the application of a force. The same torque can be produced by applying a small force at a larger distance (with more leverage) or by applying a larger force closer to the point about which the object has to rotate. These two examples are shown in Fig. 1. In the case of the hammer pulling the nail, a small force applied at the end of the handle translates into a larger force being exerted on the nail at a smaller distance from the point where the nail is fixed to the board. In the second example the weight on the palm of the hand is at a greater distance from the elbow. This requires the muscles to apply a larger force at a smaller distance, usually less than 5 cm from the elbow. These are both examples of lever action—force applied at a distance from a fulcrum or pivot point or axis of rotation. A force applied as described in the above examples results in a torque on a body. Torque usually produces a rotation of a body.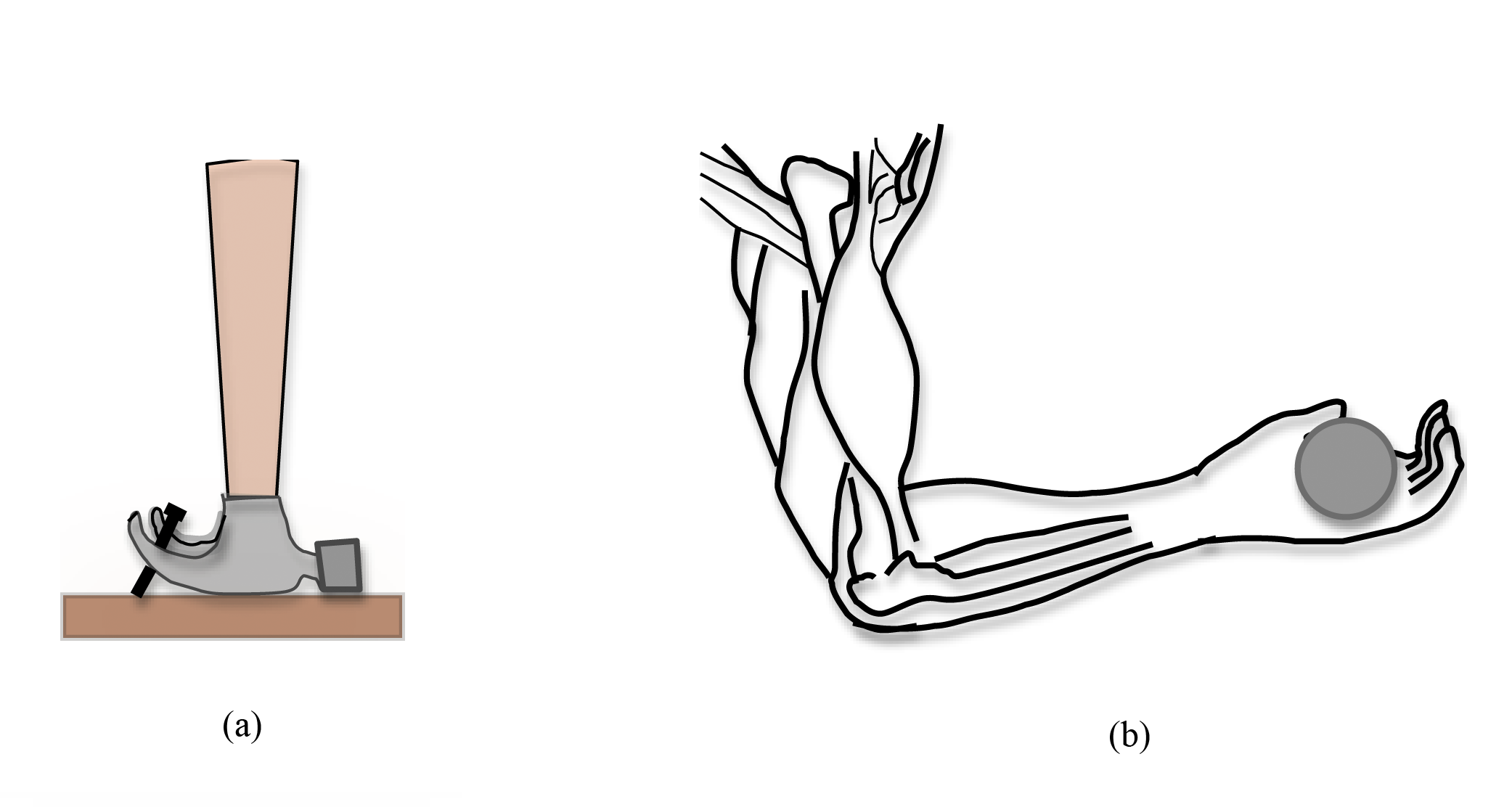

Figure 1: Two examples of torque

Discussion of Principles

Torque is a measure of the turning effect of an applied force on an object, and is the rotational analogue to force. In translational motion, a net force causes an object to accelerate, while in rotational motion, a net torque causes an object to increase or decrease its rate of rotation. Torque

is the product of the applied force and the perpendicular distance from the pivot point to the line of action of the force and is measured in units of N·m.

( 1 )

τ = Fr

_⊥

where

r_⊥

is sometimes called the "lever arm." Note: Torque has the same units as work, i.e., force times distance. Torque and work, however, are entirely different physical concepts; the fact that they have the same units is a coincidence.

Calculation of torque

Consider the irregularly shaped two-dimensional object shown in Fig. 2a.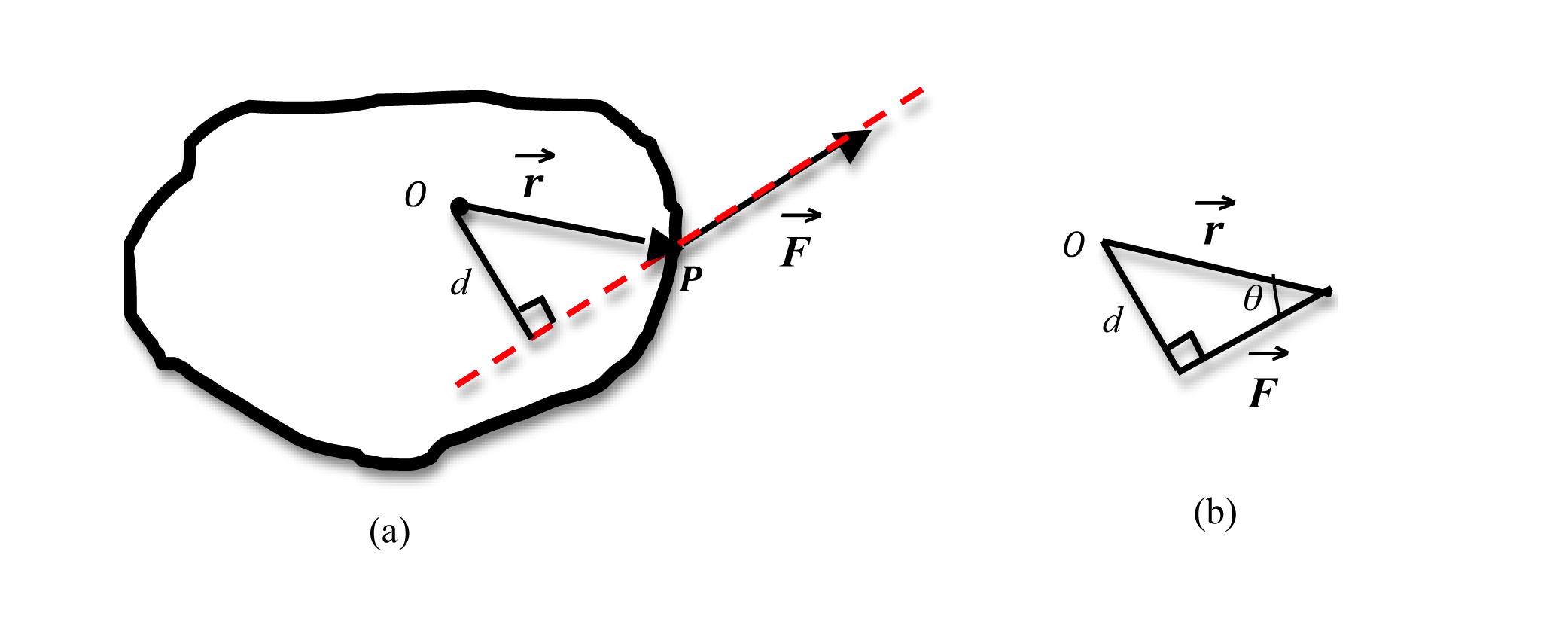

Figure 2: Illustration of lever-arm concept

A force F is applied to the object at the point P, for example, by a string attached there. The object is free to rotate about the point O by a nail driven through it at that point, but not free to have translational motion. The steps needed to calculate the torque on the object about the point O is outlined below.

Sketch a line through the force. This dashed line in Fig. 2a represents the line of action of the force.

Draw a perpendicular line from the axis of rotation O to the line of action of the force. This line, marked d in Fig. 2, represents the lever arm.

Notice that when the line of action of the force moves closer to the pivot point, the lever arm d decreases as shown in Fig. 3a and 3b. In Fig. 3c the line of action of the force passes through the pivot point. In this case the lever arm is zero and therefore the torque will be zero as well.

Figure 3: Dependence of lever arm on point of application of force

Since the lever arm d makes a right angle with the line of action of the force, the three quantities, d, F, and r make a right triangle. This triangle has been redrawn in Fig. 2b. From this triangle we see that the lever arm d is given by

( 2 )

d = r sin θ

where

is the angle between

and

Equation (1) can now be written as

( 3 )

τ = rF sin θ.

Using vector multiplication, this can also be expressed as the cross product of

and

( 4 )

= r

× F

Net torque

If two or more forces are applied to an object, each force produces a torque. The rotation of the wheel shown in Fig. 4 is caused by the sum of the two torques.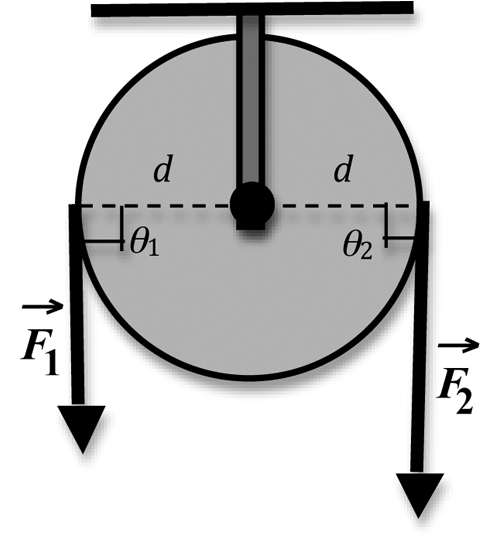

Figure 4: A wheel experiencing two torques

By convention, torques causing counterclockwise rotations are considered to be positive and torques causing clockwise rotations are negative. In the above example

₁

will produce a positive or counterclockwise torque, while

₂

will produce a negative or clockwise torque. For rotation about the center the magnitude of the net torque will be the algebraic sum of the two torques:

( 5 )

τ_total = F₁d₁ − F₂d₂.

As mentioned above, torque is actually a vector. The torque vector is perpendicular to the plane formed by the vectors

and

The right-hand rule gives the direction of the cross product of two vectors. Based on this rule positive torques, such as

F₁d₁,

are directed out of the page, while negative torques, such as

F₂d₂,

are directed into the page.

Definitions of equilibrium

Torque causes rotational motion with angular (or rotational) acceleration

α,

( 6 )

τ_net = Iα

where I is the moment of inertia of the system and

is the angular acceleration. This equation is the angular equivalent of Newton's second law:

( 7 )

F_net = ma.

When the net torque is zero, the object will not change its state of rotational motion—i.e., it will not start rotating or stop rotating or change the direction of its rotation. It is said to be in rotational equilibrium. If the sum of the forces acting on the object is also zero, the object is in translational equilibrium and will not change its state of translational motion, that is, it will not speed up or slow down or change its direction of motion. Whenever both of these conditions

( 8 )

	τ

= 0 and

	F

= 0

are met, the object is said to be in static equilibrium.

OBJECTIVE

The objective of this experiment is to learn to measure torque due to a force and to adjust the magnitude of one or more forces and their lever arms to produce static equilibrium in a meter stick balanced on a knife-edge; use the conditions for equilibrium to determine the mass of the meter stick and the mass of an unknown object.

Equipment

Meter stick
Knife-edge
Known masses of varying values
Unknown mass
Balance

Procedure

There are three parts to this experiment. In the first part, you will balance three forces on a meter stick and show that the net torque is zero when the meter stick is in equilibrium. In the second part you will balance the weight of the meter stick against a known weight to determine the mass of the meter stick. Finally you will use the principle of rotational equilibrium to determine the mass of an unknown object. All lever arm distances are measured from the knife-edge, which serves as the point of support. You will be using rubber bands to hang the weights on the meter stick. Assume that the masses of the rubber bands are negligible.

Procedure A: Balancing Torques

Balance the meter stick on the knife-edge. The point at which the stick balances is the center of gravity of the meter stick. Enter this value on the worksheet.

Select two 200-gram masses and one 100-gram mass.

Refer to Fig. 5 and Fig. 6. Place a hanger at the 20-cm mark, a distance

x₁

cm to the left of the center of gravity and place mass

m₁ = 200 g

on it.

Place another hanger at the 65-cm mark, a distance

x₂

cm to the right of the center of gravity and place a mass

m₂ = 200 g

on it.

Enter these values in Data Table 1.

Figure 5: Three balanced torques

Figure 6: Photo of experimental set up

Calculate the torques due to

m₁ and m₂

and enter these values in Data Table 1. Be sure to include the sign of the torques.

Using the appropriate sign for each torque we can write the condition for rotational equilibrium as

( 9 )

	τ

= m₁gx₁ − m₂gx₂ − m₃gx₃ = 0

Use Eq. (9) and the values of the torques due to

m₁ and m₂

to predict the torque due to

m₃

(including its sign) and enter this value in Data Table 1.

Be sure to include the sign of the torques.

Use the predicted value of the torque due to

m₃

to predict the position of

x₃

at which the third mass

m₃

must be placed to balance the meter stick. Record this value on the worksheet.

Experimentally determine the position

x₃ of m₃

and enter this value on the worksheet.

Compare the two values for the position

x₃

by finding the percent difference between the predicted and experimental values of

x₃.

See Appendix B.

Checkpoint 1:
Ask your TA to check your set-up and calculations.

Procedure B: Finding the Mass of a Meter Stick

For this part of the experiment you will use a 200-gram mass, the meter stick and the knife-edge.

Move the knife-edge to the 25-cm mark.

You will notice that the meter stick is no longer in equilibrium. The unbalanced force is the weight of the meter stick at its center of gravity.

Experimentally find the position,

x₁

of the 200-gram mass, needed to balance the meter stick. Enter the value of

x₁

and its uncertainty on the worksheet.

In the space provided in the worksheet, sketch and carefully label a diagram of the meter stick and the 200-gram mass.

Show all the torque-producing forces. Remember that the weight of the meter stick acts at its center of gravity.

Indicate on your diagram the directions (clockwise or counterclockwise) of each torque.

Calculate the torque due to the 200-gram mass and enter this value in Data Table 2.

Use the value of the torque due to the 200-gram mass and the conditions for rotational equilibrium to determine the torque due to the mass

m₂

of the meter stick. Enter this value in Data Table 2.

Using the value of the torque determined in step 14, calculate the value of the mass of the meter stick m₂. Enter this value on the worksheet.

Calculate the uncertainty associated with the calculated mass and enter this value in the worksheet. See Appendix C.

Determine the percent uncertainty in the calculated value of the mass of the meter stick.

Use the balance to measure the mass of the meter stick.

Calculate the percent uncertainty in the measured mass of the meter stick.

Compare the measured and calculated values of the mass of the meter stick by computing the percent difference.

Checkpoint 2:
Ask your TA to check your diagram, set-up, uncertainty formula, and calculations.

Procedure C: Determining an Unknown Mass

Position the center of gravity of the meter stick over the support.

Place a 50-gram mass

m₁

at the 70-cm mark and a 200-gram mass

m₂

at the 20-cm mark.

You will tie the free end of the string to a shot bucket around the 1-cm mark and hang it over the pulley as shown in Fig. 7 and Fig. 8.

Figure 7: Set-up for determining an unknown mass

Figure 8: Photo of set-up for determining an unknown mass

In the space provided on the worksheet, sketch and carefully label a diagram of this set-up.

Show all the torque-producing forces.

Indicate on your diagram the directions (clockwise or counterclockwise) of each torque.

Calculate the torques due to

m₁ and m₂,

and enter these values in Data Table 3.

Use the values of the torques due to the two masses and the conditions for rotational equilibrium to determine the torque due to

m₃.

Enter this value in Data Table 3.

Use the equation below to calculate the uncertainty in the predicted mass of

m₃.

( 10 )

σ_m₃ =

σ_x₃m₃

x₃

	2

σ_m₁x₁

x₃

	2

σ_x₁m₁

x₃

	2

σ_m₂x₂

x₃

	2

σ_x₂m₂

x₃

	2

Calculate the percent uncertainty in the predicted mass of the shot plus bucket.

Now add small masses to the bucket until the stick balances.

Determine the mass

m₃

and the associated uncertainty of the shot and bucket using a balance.

Calculate the percent uncertainty in the experimental mass of the shot plus bucket.

Compute the percent difference between the experimental and predicted values for the mass of the shot plus bucket.

Checkpoint 3:
Ask your TA to check your set-up, diagram and calculations.