Lab 1 - Measurement of Mass, Length, and Time

Introduction

In an experiment we define and determine the relationship between physical characteristics of nature that have been observed. Measurement of those physical quantities plays a crucial role in determining how nature behaves. A measurement places a numerical value on some physical phenomenon or characteristic of a phenomenon. A measurement consists of assigning a number along with appropriate units to some property or variable of the system of our interest. In this lab you will acquaint yourself with basic scientific conventions for measuring physical quantities and for analyzing data obtained from those measurements. You will learn the proper way to use measuring devices such as a meter stick, balance, vernier caliper, and a digital stopwatch. It is not sufficient to just take measurements. It is important that you learn to account for the experimental uncertainties that inevitably arise when using a measuring instrument. To do this it is necessary to know how accurate the measurement is and how precise is the instrument that you use to make the measurement. This lab is divided into two separate activities. In the first activity, you will use a simple pendulum to experimentally determine a value for the acceleration due to gravity. In the second activity, you will determine the density of aluminum. In each case, you will learn how to analyze the data you collect from your measurements in order to obtain the value of interest.

Discussion of Principles

Acceleration of Gravity

To determine the acceleration of gravity using a pendulum, you will be required to measure the pendulum's length and its period of oscillation. A simple pendulum consists of a mass or pendulum bob tied to a string. The length of the pendulum is defined as the distance from the point of suspension of the string to the center of the pendulum bob. See Fig. 1.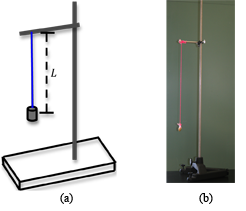

Figure 1: A simple pendulum

The period of oscillation T is the amount of time required for a pendulum to go through one complete oscillation. By "complete oscillation" we mean that the pendulum swings from the equilibrium position to one side, then the other side and back to its original starting position. When the length of a pendulum is changed, there is a corresponding change in the period of oscillation. In your physics course, you might see how to derive theoretically the mathematical relationship between the length and period of oscillation. For now, you are given the relationship

( 1 )

T = 2π

where L is the length of the pendulum and g is the acceleration of gravity. If we square both sides of Eq. (1), we get

( 2 )

T² = 4π²

You will measure the pendulum's length and period of oscillation, and use Eq. (2) to calculate a value for g. You can then compare this value with the accepted value of g = 9.81 m/s².

Density of Aluminum

You will be given an aluminum cylinder. To calculate its density, it will be necessary to determine the cylinder's mass and volume. The volume of a cylinder is given by

( 3 )

V = πr²L =

πD²

where r is the radius, D is the diameter and L is the length. Therefore the density ρ will be

( 4 )

ρ =

D²L

where M is the mass of the cylinder. You will measure the mass, length, and diameter of your cylinder (see Fig. 2), and use Eq. (4) to calculate the density.

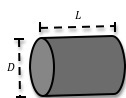
Figure 2: Sketch showing length and diameter of a cylinder

Objective

The purpose of this laboratory exercise is to:

determine the acceleration due to gravity by measuring the period of a simple pendulum, and

determine the density of the material of the cylinder by measuring the mass, length and diameter of a cylinder.

You will learn to determine the errors associated with your measurements. You will also learn to calculate the standard deviation in the measurements using Excel, determine the percent uncertainty and percent error, and evaluate your results.

Equipment

Pendulum bob
String
Stand with clamp
Protractor
Meter stick
Balance
Vernier caliper
Stopwatch
Solid cylinder

Procedure

Procedure A: Acceleration of Gravity

Attach your pendulum to the stand so that it can swing without hitting any obstructions.

Using a meter stick, adjust the length L of your pendulum to be between 60 cm and 100 cm. See Fig. 1.

Record this value on the worksheet.

Determine the uncertainty in the length measurement and record this value on the worksheet.

Note: Uncertainty values should be reported to just one significant digit.

For this exercise, you must make sure that the angle between the vertical and the pendulum is a small angle (less than about 10 degrees).

Use the protractor provided to make sure that you do not pull the pendulum by more than 10 degrees to one side.

Pull the pendulum to one side and then release it so it oscillates to and fro without any circular motion.

Using the stopwatch, measure the amount of time, t₂₀, required for the pendulum to go through 20 complete oscillations and record this on the worksheet.

The uncertainty for each stopwatch measurement is ±0.3 s. This has nothing to do with the accuracy of the stopwatch. Instead, this takes into account human reaction time that causes an uncertainty in the measurement.

Calculate the period T for one oscillation. Record this value on the worksheet.

Calculate the uncertainty σ_T in the period T and record this on the worksheet. See Appendix C.

Write the expression for the uncertainty σ_g in g. There should be two terms, one involving L and one involving T.

Use Eq. (1) to calculate the acceleration of gravity g and record it on the worksheet.

Determine the percent uncertainty in the measurement of g. See Appendix B.

Compare the experimental and accepted values of the acceleration due to gravity by calculating the percent error between the two values. Use 9.81 m/s² for the accepted value.

Checkpoint 1:
Ask your TA to check your calculations before proceeding.

Procedure B: Density of Aluminum

It is common practice to attempt to obtain a more accurate value of a measured quantity by making many measurements and then averaging them together. You will do this with the diameter of the aluminum cylinder and use the standard deviation (often denoted by σ of the set of data to determine the uncertainty in the average value.

Use the balance to measure the mass M of your aluminum cylinder and its associated uncertainty. Enter these values on the worksheet.

Use the calipers to measure its length L. See Appendix D.

Record the length and its uncertainty on the worksheet.

Note: The uncertainty in each of the quantities you measure is half of the smallest division rounded to the same number of digits as the reading itself.

Use the calipers to measure the diameter close to one end of the cylinder. Record this value as D₁ in Data Table 1, but do not record any uncertainty.

Now, just barely loosen the teeth of the calipers, rotate the cylinder 90 degrees, and retighten the teeth. Measure the diameter again and record it as D₂ in Data Table 1.

Loosen the calipers and slide them down about 1/3 of the way along the cylinder. Make two more measurements of the diameter just as you did in steps 16 and 17 above. Record these values in Data Table 1.

Take two more measurements about 2/3 of the way down the cylinder and two more at the far end of the cylinder. You should have eight diameter measurements in all.

Enter the values in an Excel spreadsheet. See Appendix E.

In Excel, calculate the average of these eight readings and the standard deviation. Record the average value of the diameter and the uncertainty (standard deviation) in the diameter on the worksheet. See Appendix E.

Write the expression for the uncertainty

σ_ρ

in the density ρ. Keep in mind that you must take into account the uncertainties of three measured quantities: mass, diameter, and length.

Using the mass and length that you measured, calculate the density of your aluminum cylinder and record this on the worksheet.

Calculate

σ_ρ

and the percent uncertainty. Record these values on the worksheet.

Compare the experimental value of the density of aluminum with the accepted value of 2.70 g/cm³ by determining the percent error between the two values. Record this on the worksheet.

Checkpoint 2:
Ask your TA to check your calculations.