Lab 2 - Capacitors

Introduction

The basic function of a capacitor is to store charge and thereby electrical energy. This energy can be retrieved at a later time for a variety of uses. Often, multiple capacitors are combined together to form a single circuit. There are two fundamental ways of connecting capacitors together: in series and in parallel. In this lab, you will explore how charge and energy are stored on both series and parallel combinations of capacitors.

Discussion of Principles

A capacitor is a set of two metal conductors separated by a small distance. Usually some type of dielectric (non-conducting) material is placed between the two conductors. An example is the parallel plate capacitor shown in Fig. 1. When connected to a voltage source, such as a battery, the two conducting plates become charged. When the battery is first connected, free electrons inside the top capacitor plate will move toward the positive terminal of the battery. This continues until the top capacitor plate is at the same potential as the positive terminal of the battery. A net positive charge, +Q, will then be on the top capacitor plate. At the same time, free electrons inside the wire connecting the negative terminal to the bottom capacitor plate will move toward the bottom capacitor plate. This continues until the bottom capacitor plate is at the same potential as the battery's negative terminal. A net negative charge, –Q, will be present on the bottom capacitor plate.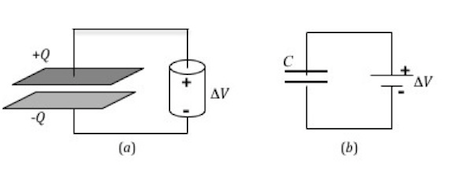

Figure 1: Capacitor circuit

Fig. 1(a) shows a parallel-plate capacitor connected to a battery and Fig. 1(b) is the schematic diagram of the same setup. Note that the symbols for a capacitor and a battery are similar but not the same. Be careful not to confuse them. Note that there are equal and opposite charges (+Q and –Q) on the two plates of the charged capacitor. For convenience, we simply refer to the magnitude of the charge and say that the capacitor has a charge Q on it. Also note that since the top capacitor plate is at the same potential as the positive battery terminal and the bottom plate is at the same potential as the negative battery terminal, the potential difference between the capacitor's two plates is the same as the potential difference

ΔV

across the terminals of the battery. The amount of charge deposited on a capacitor is directly proportional to the potential difference placed across its plates. This can be written as

( 1 )

Q = CΔV

where the proportionality constant C is known as the capacitance of the capacitor and is measured in units of Farads (F). The capacitance depends on the particular geometry of the capacitor as well as the type of dielectric material used. If you were to remove the battery from a charged capacitor, the charges would stay on the plates, and a potential difference would remain between the two plates of the capacitor. Therefore, we say that the capacitor "stores" electrical energy. The amount of energy stored in a charged capacitor can be calculated using the formula

( 2 )

E =

C(ΔV)².

By using Eq. (1), this formula can be rewritten in two other equivalent forms.

( 3 )

E =

Q²

( 4 )

E =

QΔV

Capacitors Connected in Parallel

Frequently we want to combine multiple capacitors into one circuit. One way to combine capacitors is to connect them in parallel as shown in Fig. 2. Note that the top plates of both capacitors are connected to the positive terminal of the battery, and the bottom plates of both capacitors are connected to the negative terminal. Therefore, the potential difference across each individual capacitor will be the same as the total potential difference placed by the battery across the whole parallel arrangement.

( 5 )

ΔV₁ = ΔV₂ = ΔV

Each individual capacitor will store different charges, Q₁ and Q₂. The total charge placed on the entire parallel arrangement by the battery is then

( 6 )

Q_total = Q₁ + Q₂.

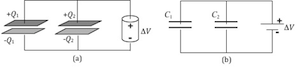
Figure 2: Sketch and schematic of two capacitors in parallel arrangement

The total capacitance of the parallel arrangement,

C_total,

will be different from either of the individual capacitances, C₁ or C₂. To determine this equivalent capacitance, first note that we can use Eqs. (1) and (5) to write

Q_total = C_eqΔV, Q₁ = C₁ΔV, and Q₂ = C₂ΔV.

Substituting these expressions into Eq. (6) and canceling the common factor of

ΔV

we get

( 7 )

C_total = C₁ + C₂.

This is typically called the equivalent capacitance and is denoted by

C_eq.

So for a parallel arrangement made up of N different capacitors,

C_eq = C₁ + C₂ + C₃ + ... + C_N.

The energy

E_total

stored in the parallel arrangement can be calculated using Eq. (2) as

( 8 )

E_total

C_eq(ΔV)²

(C₁ + C₂)(ΔV)²

C₁(ΔV)² +

C₂(ΔV)².

Notice that the total energy stored in the parallel arrangement is equal to the sum of the energies stored in each of the individual capacitors.

Capacitors Connected in Series

Another way to combine capacitors is to connect them in series as shown in Fig. 3. When connected to a battery, the bottom plate of the first capacitor C₁ will store a charge –Q and the top plate of the second capacitor C₂ will store a charge +Q. We see then that the total charge placed on the overall series arrangement by the battery is Q. Notice that the top plate of C₁ and the bottom plate of C₂ are connected by a conducting wire, forming a single H-shaped conductor. This conductor is not connected to the battery, so the battery cannot directly provide charge to it. Instead, the negative charge –Q on the bottom plate of C₁ and the positive charge +Q on the top plate of C₂ will cause free electrons in the H-shaped conductor to move to the top. The result is an induced net charge of +Q on the top plate of C₁ and an induced net charge of –Q on the bottom plate of C₂. Therefore, both capacitors will have the same charge Q, which is the same as the total charge on the entire arrangement.

( 9 )

Q_total = Q₁ = Q₂

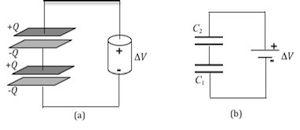
Figure 3: Sketch and schematic of two capacitors in series arrangement

The bottom plate of C₁ is at the same potential as the negative terminal of the battery, and the top plate of C₂ is at the same potential as the positive terminal. The H-shaped conductor will have a potential somewhere in between these two values. So, moving from the top plate to the bottom plate of C₂, the potential will drop by

ΔV₂.

Then, moving from the top plate to the bottom plate of C₁, the potential will drop by

ΔV₁.

The potential difference

ΔV

across the entire series arrangement is equal to the sum of the potential differences across each individual capacitor.

( 10 )

ΔV = ΔV₁ + ΔV₂

We can use Eq. (1) to write the potential difference across the individual capacitors and the parallel arrangement as

( 11 )

ΔV =

Q_total

C_eq

( 12 )

ΔV₁ =

Q_total

C₁

( 13 )

ΔV₂ =

Q_total

C₂

Substituting these expressions into Eq. (10), using Eq. (9), and canceling the common factor,

Q_total,

gives

( 14 )

C_eq

C₁

C₂

The energy stored in the total series arrangement can be calculated using Eq. (4).

( 15 )

E_total

Q_totalΔV

Q_total(ΔV₁ + ΔV₂)

Q_totalΔV₁ +

Q_totalΔV₂

Note that this is the sum of the energies stored in each individual capacitor. Listed below are the equations governing voltage distribution, charge distribution, equivalent capacitance, and energy storage for the two types of arrangements.

Parallel Arrangement

Series Arrangement

ΔV = ΔV₁ = ΔV₂

ΔV = ΔV₁ + ΔV₂

Q_total = Q₁ + Q₂

Q_total = Q₁ = Q₂

C_eq = C₁ + C₂

C_eq

C₁

C₂

E_total = E₁ + E₂

Objective

The objective of this experiment is to study the characteristics of capacitors in series and parallel arrangements and to qualitatively investigate the energy stored in such arrangements.

Equipment

Signal interface with power output
Capstone software
Multimeter
Capacitance meter
Two different capacitors
One LED
Stopwatch

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

This lab consists of four parts. The first procedure is a qualitative investigation of the energy stored by different arrangements of capacitors. You will charge both a series arrangement and a parallel arrangement of capacitors and in each case use the stored energy to light up a small LED bulb. You will predict which arrangement stores more energy based on the amount of time the bulb remains lit. In the remaining procedures, you will use a capacitance meter and a voltmeter to make quantitative measurements on parallel and series arrangements of capacitors. You will compare your data with the theoretical equations for voltage distribution, charge distribution, equivalent capacitance, and energy storage.

Checkpoint :
Before connecting the power supply to the circuit, ask your TA to check your circuit connections to make certain that your capacitors are connected correctly.

Procedure A: Lighting an LED

Open the appropriate Capstone file associated with this lab. The screen should contain a signal generator window similar to the one shown in Fig. 4. Banana plug cables should be connected to Output 1.

In the Signal Generator window select DC. Set the DC voltage to 5.0.

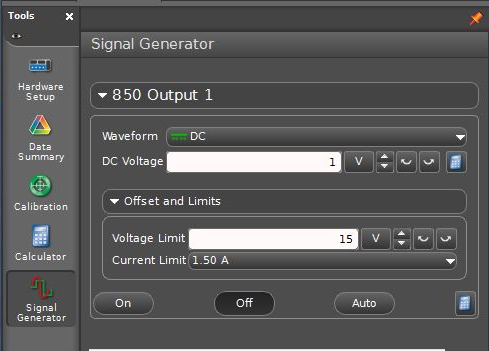
Figure 4: Signal Generator window

Click ON.

Discharge both of your capacitors by shorting them out for at least 10 seconds as shown in Fig. 5.

You can check to see if the capacitors are fully discharged by using the voltmeter to read the potential difference across each capacitor. See Appendix K.

The readings should be very close to 0.0 volts.

Figure 5: Discharging a capacitor

Connect the two capacitors in series. They must be connected so that the arrows printed on each capacitor are facing the same direction as shown in Fig. 6.

The red output lead must be connected to the notched end of one capacitor (this is also the end with the black face) while the black lead must be connected to the end that has the arrows pointing toward it (this is the end with the silver face). This will charge the capacitors.

Figure 6: Circuit diagram and photo of capacitors in series

Disconnect the power output from the circuit by removing the red and black leads from the capacitors. DO NOT turn off the power output or set its voltage to zero.

Connect the LED to the capacitor arrangement as shown in Fig. 7.

The red and black LED leads should be connected the same way the red and black power amplifier leads were connected.

Immediately begin timing how long the LED remains lit. Record the time on the worksheet.

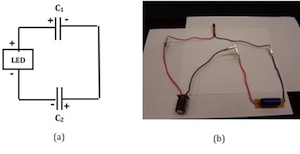
Figure 7: Circuit diagram and photo for LED connection

Disconnect your series arrangement and fully discharge both capacitors.

Connect the two capacitors in parallel. Again, the arrows should point in the same direction as shown in Fig. 8.

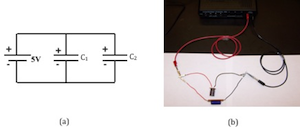
Figure 8: Circuit diagram and photo of capacitors in parallel

Repeat steps 3 through 6 for the parallel arrangement referring to Fig. 8. Record the time for the parallel arrangement on the worksheet.

Now use just the

1000−μF

capacitor and see how long the LED remains lit. Record this time on the worksheet.

Checkpoint 1:
Ask your TA to check your work before proceeding.

Procedure B

Set the capacitance meter to the appropriate setting.

Measure the capacitance of each individual capacitor. Record the capacitances in Data Table 1.

Connect the two capacitors in parallel.

Using the capacitance meter, measure the total (or equivalent) capacitance of the parallel arrangement. Record this value in Data Table 1.

Leave the parallel arrangement connected and discharge the capacitors by shorting them out one at a time.

Use the multimeter to make sure they are fully discharged. See Appendix K.

Connect the parallel arrangement to the power output leads as shown in Fig. 8.

Turn the multimeter on and switch to the proper DC voltage scale.

For this step, it is important that you do not touch the capacitor leads when you are measuring the voltage. You are a resistor, just like the LED, so you are capable of discharging the capacitor by touching it.

Measure and record the potential difference

ΔV₁ and ΔV₂

across C₁ and C₂, respectively. Record these values in Data Table 1.

Measure the potential difference

ΔV_p

across the parallel arrangement and record this in Data Table 1.

Using the measured values of capacitance and voltage and Eq. (1), calculate the charges for the individual capacitors and the parallel arrangement. Record these values in Data Table 1.

Using Eqs. (2) and (8)and the measured values of the capacitances, calculate the energy stored in each individual capacitor and the parallel arrangement. Record these values in Data Table 1.

Using Eq. (7), calculate the theoretical equivalent capacitance for the two capacitors in parallel. Record this value on the worksheet.

Calculate the percent difference between the theoretical value and the measured value (see Data Table 1) of the equivalent capacitance. See Appendix B.

Using Eq. (6), calculate the theoretical total charge for the two capacitors in parallel. Record this value on the worksheet.

Calculate the percent difference, between the theoretical value and the measured value of the total charge and record this on the worksheet.

Checkpoint 2:
Ask your TA to check your table and calculations.

Procedure C: Capacitors in series

Record the previously measured capacitances of the two capacitors in Data Table 2.

Connect the two capacitors in series.

Using the capacitance meter, measure the total capacitance of the series arrangement. Record this value in Data Table 2.

Leave the series arrangement connected and discharge the capacitors by shorting them out one at a time. Make sure they are fully discharged.

Connect the power amplifier to the arrangement as shown in Fig. 6.

Measure the voltage across each individual capacitor. Record your measurements in Data Table 2. Again, be careful not to touch the leads when recording the voltages.

Measure the voltage

ΔV_s

across the entire series arrangement. Record this value in Data Table 2.

Using the measured values of capacitance and voltage, calculate the charge stored on each capacitor. Record these values in Data Table 2.

Using measured values for the total capacitance and voltage and Eq. (1), calculate the charge in the series arrangement. Record these values in Data Table 2.

Using Eqs. (2) and (15) and the measured values of the capacitances, calculate the energies stored in the individual capacitors and the series arrangement. Record these values in Data Table 2.

Calculate the theoretical capacitance for the series arrangement using Eq. (14). Record this value on the worksheet.

Calculate the percent difference between the theoretical value and the measured value (from Data Table 2) of the equivalent capacitance. Record this on the worksheet.

Using Eq. (10), calculate the theoretical voltage for the series arrangement. Record this value on the worksheet.

Calculate the percent difference between this theoretical value and the measured value (from Data Table 2) of the total voltage and record this on the worksheet.

Checkpoint 3:
Ask your TA to check your table and calculations.