Print

Faraday's Law

Purpose

Equipment

  • Virtual Faraday's Law Apparatus
  • Pencil

Simulation and Tools

Open the Virtual Faraday's Law Apparatus simulation to do this lab.

Theory

We're surrounded in our daily lives by devices using Michael Faraday's and Joseph Henry's discovery that a change in the magnetic flux through a loop of wire will induce an emf in the loop. This allows for physically disconnected devices to interact via electromagnetic fields. A rechargeable electric toothbrush is a simple example. The toothbrush sits on a charging base with a vertical shaft that fits into a matching hole in the bottom of the toothbrush. Primary coils in the base carry an alternating current, which produces a varying magnetic field, which passes through a secondary coil in the brush handle. The induced emf in this secondary coil generates a current, which is used to charge the battery sealed in the handle. The original models plugged straight into the AC! We'll be working with a similar arrangement in this lab. In our case, the primary coil is a solenoid large enough to hold our measurement instruments—a Hall probe to directly measure the magnetic field, and two different sizes of pickup coils (think guitar pickup).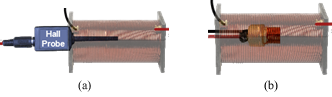
Figure 1: (1a) Hall Probe, (1b) Pickup Coil
We'll show that if the solenoid is long enough the field along its central axis and near its center is uniform in magnitude and direction. The field in this central region is given by
( 1 )
Bsol = μ0nI
where B is the magnitude of the magnetic field in teslas,
μo = 4π × 10−7 T · m/A
 is the permeability of free space, n is the number of turns per meter of length (N / L) of the solenoid and I is the solenoid current in amps. For our solenoid
N = 570
 turns and
L = 0.170 m.
 When using the pickup coil, the flux, Φ, through the coil depends on the magnitude of the field, Bsol, the cross-sectional area of the coil, A, and the cosine of the angle between the vector B, and a vector A, normal to the area.
( 2 )
Φ = B · A = BA cos(θ)
The flux is measured in Webers (Wb), B is the field (here provided by the solenoid) passing through the coil in teslas, and A is the cross-sectional area of the coil in m2.
1 Wb = 1 Tm2.
 In this lab, B is always parallel to A, so BA cos(0°) = BA. (See Figure 2b.)
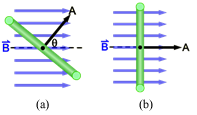
Figure 2: Edge-on views of a coil (green) rotating around an axis (black dot) normal to the page.
When there is a change in flux through a coil, Faraday's Law allows us to calculate the emf induced in the coil with N loops as follows.
( 3 )
emf = −N
ΔΦ
Δt
In our particular experiment, the area of the coil is fixed so the flux change depends only on the change in the magnetic field, B, through the coil. Faraday's law simplifies in this case to
( 4 )
emf = −NA
ΔB
Δt
.
You'll want to refer back to equation 4 frequently in this lab. It's the source of many answers.
We will first investigate the field of the solenoid and then identify different ways of changing the flux through the pickup coil. Finally, we'll study the induced emf produced by this changing flux.
Note:

For brevity, "B" will often be used in this lab to refer to the magnitude of the magnetic field.

Explore the Apparatus

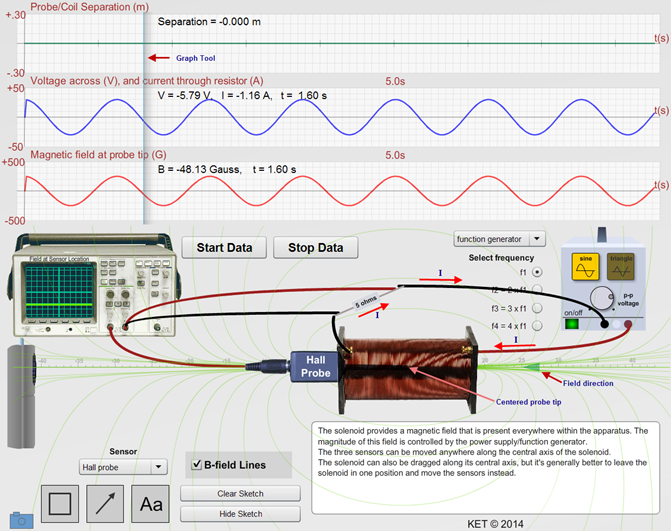
Figure 3: Faraday's Law Apparatus
Most of the important parts of the apparatus are labeled or recognizable from their images. The function generator at the right looks somewhat different when in DC mode where it's referred to as a power supply. And the Hall probe inserted into the solenoid will be replaced by a coil of wire called a pickup coil at some points in the lab. The green triangle to the right of the solenoid indicates the instantaneous direction of the solenoid's field. The top graph always measures the distance between the center of the solenoid and the tip of the Hall probe or the center of the pickup coil, depending on which one is in use. The solenoid current is determined by placing a 5.00-Ω resistor in series with it and then measuring the voltage drop across the resistor with the computer interface at the left. This voltage drop and current are plotted in the middle graph. The bottom graph has two responsibilities depending on which sensor is in use.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

PDF file

I. Investigation of the Magnetic Field of a Solenoid

You'll frequently be asked to set the "DC power supply" to a certain voltage, usually 30.00 V or 50.00 V. Why so precise? You'll want to try to set it to exactly the suggested value mainly to produce consistent results in different parts of the lab. You'll often record a measurement when, for example, the voltage is 30.00 V and then look back at a result you got earlier with the same setting. If you used 30.02 V on one occasion and 29.98 V on another, results that would be expected to match will disagree. So what's so hard about that? To set the voltage you first click on the little circular handle on the knob as shown in Figure 4a. You then drag the handle around in a circle to turn the knob. Try setting the voltage to 30.00 V. Aarghh! It's impossible. Actually there's a trick that you've probably learned in other pieces of our apparatus. Here's a tutorial for this one. Setting the voltage to 30.00 V seems difficult at first since the voltage changes by large amounts with a small movement of your pointer. However, clicking on the handle and dragging away from the center of the knob effectively enlarges the knob, allowing for a more precise adjustment. (See Figures 4b-c.) Try it. You can drag all the way to the edge of your computer screen. Or even onto a second monitor. Alternate interpretation: Use chopsticks for increased precision. Still a bit difficult? Try reducing the size of your browser window and moving it to the left side of the screen. You can now drag right out of the browser window and as long as you keep the mouse button down, you're still in the lab. Once you get the voltage set you can resize the browser.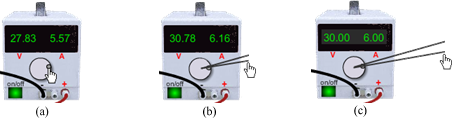
Figure 4: Fine Adjustment of Voltage and Current

A. The Magnetic Field at the Center of a Solenoid Carrying a Direct Current

1
From equation 1, we know that the magnitude of the magnetic field at the center of a solenoid is given by
Bsol = μonI.
Your current should be 6.00 A. Calculate the theoretical value for the magnetic field at the center of the solenoid using equation 1.
2
The solenoid's field can be measured experimentally using a Hall probe, which measures magnetic fields using the Hall Effect. Select the Hall probe from the Sensor list. The probe measures the magnetic field at its tip so it's important to place the tip at the center of the solenoid in this part of the lab. Either the solenoid or the probe can be dragged horizontally to adjust this alignment. We want to keep the solenoid in one location so if you've moved it, drag it to where its left end is at about the 0-cm point and leave it in place. (This is the default location.) Then drag the probe until its tip is near the center of the solenoid. (The solenoid is magically somewhat transparent.)
3
Click the Start Data button. (In the future this instruction will be abbreviated to simply Start Data.)
4
Three graphs are produced. The top one records the separation distance between the center of the solenoid and the tip of the probe when the probe is in use. This graph should be a horizontal line nearly or exactly coincident with the horizontal axis. If they're coincident, you have the probe aligned just where it needs to be. That's a tough call. But try this. Click on the Graph Tool, the vertical line that crosses all three graphs. Note the readings to the right of the Graph Tool. You should see something like "Separation = 0.020 m." This is a more precise reading of the value that you want to be equal to zero. Always use this tool for alignment. Here's how. Drag the Graph Tool over near the left end of the graph. Start Data. The graph trace will now quickly arrive at the Graph Tool. If it reads a separation of more than 2 mm, adjust the probe's location a bit and retry.
5
Once you have a good run with a small separation, have a look at the middle graph. It records the voltage drop across the 5.00-Ω resistor in series with the power supply and solenoid. A wire from each side of the resistor connects to the computer interface, which measures this voltage drop. (This parallel connection diverts a negligible current due to its large resistance.) From the horizontal blue line and the scale of the graph you should read a constant potential difference of about 30.00 volts. Since the resistor has a value of 5.00 Ω, the resistor current would be the voltage drop divided by 5.00 Ω. Thus it should be about 6.00 A. This is the current through the solenoid, which is in series with the resistor.
6
The Graph Tool provides a more precise reading of the voltage drop across the solenoid and the current through it. So we'll always use it for taking data. Drag this tool from side to side. Since the voltage drop and current are both constant, the only change you see is the time reading. So the graph is plotted over time and the Graph Tool allows you to easily read current and voltage drop at the time of your choosing. As you'll soon see, our currents and voltages won't stay constant for long.
7
The bottom graph displays the magnetic field measured by the probe at its tip. This should be constant in this case. Record this value in both Gauss and Tesla units. Remember 1 Gauss = 10–4 Tesla. You'll use Teslas in your calculations elsewhere in this lab. Round the experimental values to the nearest Gauss.
8
Calculate the percent error between the theoretical (calculated in Step 1 from equation 1
Bsol = μ0nI
) and experimental (measured with the probe) values for the magnetic field at the center of the solenoid.
You should have found these values to be with a few percent of each other. If not, try again.

B. Variation of the Magnetic Field Along the Axis of the Solenoid

In this lab we're primarily interested in the effects of a changing magnetic flux through a coil of wire. There are a number of ways of producing a changing flux. Some involve changing a magnetic field over time but others involve fixed magnetic fields with some mechanism for changing what part of that field passes through the coil. We'll start with the latter case by observing the effect of moving a coil along the axis of the solenoid. In order to interpret what we observe we first need to know how our magnetic field varies with position. In the preceding section you measured the magnetic field at the center of the solenoid. We now need to look at its field all along its central axis.
1
Adjust the DC power supply to 50.00 V. Make sure that the solenoid's left end is still at approximately the 0-cm point. Don't Start Data until you're instructed to do so.
2
Turn on the "B-field Lines" using the check box. A two-dimensional approximation of the solenoid's magnetic field is shown in green. The lines entering and exiting the ends of the solenoid are very compact and nearly parallel indicating that the field is relatively strong near the ends and inside. But otherwise it looks pretty complex. Imagine moving a coil through this field. Since the field varies along any path you might choose, the flux through the coil would be constantly changing. Thus an emf would be easily generated. We're going to limit our study to motion along the central axis of the solenoid.
3
Switch to the short pickup coil from the Sensor list. Move it from side to side. How does the field it encounters vary with its position along the solenoid axis? More specifically where does it change most quickly? most slowly? Clearly we need to know more about this complex field. The field lines provide only a general picture of our field.
4
Replace the pickup coil with the Hall probe. Turn off the "B-field Lines".
Let's investigate how this field varies with its position along the central axis of the solenoid using our Hall probe and Graph Tool.
5
Drag the probe all the way to the left. Start Data. Drag the probe slowly to the right at a constant speed. The top separation graph should rise steadily. Look at the bottom graph—the magnetic field measured at the probe tip vs. time. Since the probe moved at a fairly constant speed, this graph is also a good approximation of the magnetic field vs. position. The field clearly varies with distance from the center of the solenoid.
6
There should be one obvious maximum and two minimum points or horizontal line segments on your magnetic field graph. Let's look more closely by taking a set of five magnetic field readings—at the maximum distance from the solenoid on each side, at each end of the solenoid, and at its center.
  • a
    Move the Graph Tool to approximately the 1.0-s point. Drag the probe all the way to the left. Start Data but leave the probe where it is. The bottom graph will fill up with a constant reading for the magnetic field at the extreme left position, Bmin(left). Be sure you're clear on that. Your graphs are all plotted vs. time. They only give a good visual representation of the variation of each value vs. position when you moved the probe at a constant speed. You're now just measuring the field at the tip of the stationary probe. Record that value in the first column in Table 1.
  • b
    Move the probe to the far right and Start Data to measure Bmin(right).
  • c
    Repeat for the center of the solenoid, Bsol(center).
  • d
    The measurements at the two ends of the solenoid are a bit more problematic given the slightly askew photograph of the solenoid. You want to have the probe tip just crossing the plane of the end-most wraps of wire for these two measurements. Move the probe until its tip just disappears behind the left end plate of the solenoid. If you now slowly move it to the right you can just see the end of the probe peek through between the end plate and the first winding. That's where you want to measure Bsol(left). The other end requires more guesswork. Just do your best.
  • e
    Let's now put these readings in context by adding them to the screen using the Sketch label tool sketch label tool icon . First we'll recreate the full graph of the field from the left end to the right end of the probe's range of motion. Drag the probe all the way to the left. Start Data. Drag the probe slowly to the right at a constant speed. The separation graph should rise steadily. Repeat until you get a fairly straight separation line that takes at least 5 seconds to draw. This takes patience.
7
You now need to add your five pieces of data to the graph and then take a Screenshot to upload. Here's how.
  • a
    Drag the Graph Tool all the way to the left. Slowly move it to the right until you find the last point that gives a reading equal to your Bmin(left) value. That is, the last point before the reading began to climb above the minimum value. Use the Sketch label and arrow tools to indicate that point as shown in Figure 5. Use your own reading for the magnetic field.
Figure 5: Bmin(left)
  • b
    Continue with the other four readings to label each point on the graph. As you drag the Graph Tool across the screen, it will display the magnetic field value at each point. Actually, it doesn't save data for every point but you can estimate the correct positions. Use the Sketch tools to label these and include the magnitude of the magnetic field at each location in Gauss. The last data point will be at the point where you get the first Bmin(right) reading.
  • c
    Because of the size of the text, you'll have to stack some of the labels to make them all fit. See Figure 6. In that figure you'll also see that the labeled points will not be symmetrically spaced as they actually should be. This is due to the difficulty of moving the probe at a constant speed. The steadier your mouse motion, the closer it approximates a magnetic field vs. position graph. If you wanted to do some serious reverse engineering you could use the separation vs. time graph, which shows the steady increase in speed that produced Figure 6. Hopefully you have better things to do with your time.
  • d
    Take a Screenshot of your magnetic field graph and save it as "Faraday_Bmin_max.png". Upload it and/or print it out and attach it to your lab report to turn in. It should look something like Figure 6.
Figure 6: Magnetic Field at 5 Key Positions Along the Solenoid Axis
8
How would you describe the variation of B in the middle third of the length of the solenoid?
Clearly the magnetic field is strongest at the center of the solenoid and drops off as you move away from the center. We'll take advantage of this relatively constant B during the rest of this lab by working near the center of our solenoid.

II. The Induced Emf in a Coil in a Varying Magnetic Field

The Hall probe is a transducer that measures the strength of a magnetic field. We'll now look at another device that reacts in a different way to a magnetic field. A coil of wire doesn't respond to a magnet field but rather to a change in magnetic flux through its ends. Such a coil is commonly called a pickup coil or a search coil. A guitar pickup is a well-known example.
1
Set the DC voltage to 50.00 V. Select the short pickup coil and drag it to the far left.
2
Turn on the "B-Field Lines." When we speak of the magnetic field strength, B, we're actually referring to the magnetic flux density. The green "B-field Lines" representing the field in our apparatus vary in density (spacing) in the same way that the strength of the field varies spatially.
3
When located at the far left, maybe six lines pass through the pickup coil. Drag it slowly to the right and notice how increasingly more lines pass through it. The density of the lines corresponds to B, hence the term flux density. The number of lines passing through the coil corresponds to the magnetic flux (flow) through the coil, Φ ("fi"). Thus the flux depends on the density of the lines and the cross-sectional area of the coil.
As described in the theory section, when the magnetic field is normal to the cross-sectional area of the coil, the flux can be written as
( 5 )
Φ = BA.
This will always be the case with this apparatus.

A. Initial Exploration of Induced Emf

1
Position the solenoid so that its left end is at about the 0-cm mark (the default position).
2
Turn on the DC power supply and set the current to 3–4 amps.
3
Turn on the "B-field Lines." Note the direction of the solenoid field along its axis—to the right. Turn off the "B-field Lines."
4
Move the pickup coil somewhere inside the solenoid.
5
The coil, which is connected to the computer interface, has a magnetic field passing through it.
6
Above the bottom graph select the "5 mV" radio button to set the Pickup EMF (V) graph scale. A maximum reading on this scale represents an induced emf of 5 mV.
7
Start Data. Boring.
The bottom graph, Pickup EMF (V), displays the induced emf in the pickup coil. Why does it read a steady zero? An induced emf is produced when the flux through a coil changes over time.
emf = −N
ΔΦ
Δt
 = −NA
ΔB
Δt
And since the current isn't changing, we know from
Bsol = μonI
 that B is not changing. The coil cross-sectional area is also unchanged. (If we could rotate the coil we could produce an emf. That's how an electric generator works.)
1. Induced Emf Due to the Motion of a Coil Relative to a Field. Warning! Wiggling and jiggling ahead.
1
Start Data again. This time jiggle the coil from side to side at various points along the axis. Specifically, observe the emf graph when jiggling the coil at the far left, the left end of the solenoid, the center of the solenoid, the right end of the solenoid, and the far right. Leave about 0.5 seconds between jiggles. Repeat this until you get a good trial showing the five different results all on one graph. (This would have looked great blown up and glued to your tri-fold poster for that horrible science project that went so wrong in 8th grade. When that weird lady came by to ask you to discuss it you could have engaged her in an interpretive dance performance of your project just when the local news guy with the big hair came by. Too bad.)
2
Using the Sketch label tool, add the phrases "far left," "left end solenoid," "center solenoid," "right end solenoid," and "far right." Put these labels beneath the matching parts of the figure. See Figure 7 for guidance.
Figure 7: Induced Emf Due to Motion of the Coil
3
Save your graph as "Faraday_5_points.png". Upload it and/or print it out and attach it to your lab report to turn in.
4
Either a change in B, or in A, or both, over time, has to be responsible for this induced emf. A, the cross-sectional area of the coil is fixed, so it must be the field, B.
5
Why is B changing when you jiggle the coil?
6
With steady jiggling, where along the solenoid axis is the greatest emf produced? Why? (Look back at the graph you created in Part IB (Figure 6). And re-read the note about equations 3
emf = −N
ΔΦ
Δt
 and 4
emf = −NA
ΔB
Δt
.
.)
7
As shown by Figure 6, the solenoid's field is at a maximum near its center and nearly zero far away from the solenoid. Why is the emf produced at both these places so small?
This is a surprising result. Since the magnetic field is required to produce the emf you'd think that the more field, the more the emf. But it's the rate of change of the flux, not the flux itself. Or, since it's just the magnetic field, B, that's changing, it's the rate of change of B, not B itself. There's a type of rechargeable flashlight that works on this principle. You shake it and a permanent magnet moves back and forth through a coil. A rather annoying way to charge a battery. 2. Induced Emf Due to a Change in Solenoid Field Due to a Change in Solenoid Current Here's another way to induce an emf in our coil. Move the pickup coil so that its center coincides with the center of the solenoid according to the Graph Tool. The Graph Tool plots the location of the center of the coil relative to the center of the solenoid.
8
Set the Pickup EMF (V) voltage scale setting to "50 mV."
9
Turn the "B-field Lines" on.
You're now going to use the knob on the DC power supply to produce positive and negative changes in current. By rotating the knob from very roughly 8 o'clock to 10 o'clock, pause briefly, then to 2 o'clock, pause briefly, then to 4 o'clock, we can change the current from roughly –10 A to –3 A to +3 A to +10 A. You won't even get close to these numbers, but that's OK. These steps each involve positive changes in current, ΔI. And since
Bsol = μ0nI,
 there should be positive changes in B, ΔB.
10
Rotate the knob through this sequence of currents and watch the magnetic field lines and the direction arrows. The magnetic field changes from strong negative (left) to weak negative to weak positive (right) to strong positive. All these positive changes match our prediction.
11
Turn off the "B-field Lines."
12
Select the Hall probe and put its tip at the center of the solenoid.
13
Adjust the current to –10 A. Start Data. Change the current quickly through our sequence of four currents with brief pauses at each current. You should find something like Figure 8. The currents were found using the Graph Tool.
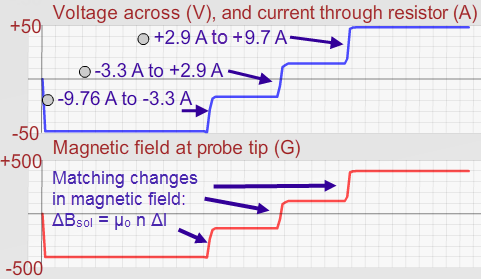
Figure 8: Change in Solenoid Magnetic Field Due to Quick Changes in Solenoid Current
What would you expect the graph to look like if you used the pickup coil? From equation 4
emf = −NA
ΔB
Δt
.
 we know that positive changes in magnetic field should produce negative emfs. How about Δt? Where on our graph is the Δt that goes in equation 4? Δt was the tiny time we took to change the current. So the emf would be negative, very large in magnitude, due to short Δt's, and it would happen right when we abruptly change the current.
emf = −NA
ΔB
Δt
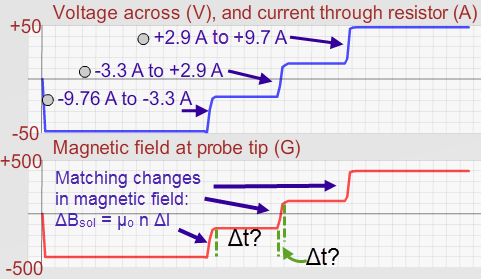
Figure 9: Change in Solenoid Magnetic Field Due to Quick Changes in Solenoid Current, with Δt
14
Let's make it happen. Switch to the pickup coil. Center it inside the solenoid using the Graph Tool.
15
Adjust the current to –10 A. Start Data. Change the current quickly through our sequence of four currents with brief pauses at each current. Perfect! Large, negative voltages, and very quick.
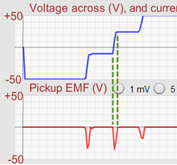
Figure 10: Induced Emf Due to Quick Changes in Solenoid Current
16
What if you went backwards through the currents, and made the jumps take longer? Describe what would be different about the return trip with the slower current changes.
17
Create a graph to show this comparison by recording the quick trip up in current followed by the slow trip back down in current. Be sure to allow brief intervals between the current changes.
18
Take a Screenshot of your voltage and emf graphs and save it as "Faraday_Emf_steps.png". Upload it and/or print it out and attach it to your lab report to turn in. Sketch your graphs on the empty graph below.
Figure 11: Faraday emf steps
This looks like a good way to produce a large emf. But jiggling the power supply knob is not so great, however. Let's automate the change in current.

B. Using the Function Generator to Vary the Field in the Solenoid

1
Switch to the Hall probe, and set its tip at the center of the solenoid.
2
Turn the "B-field Lines" on.
3
Set the DC voltage to 30.00 V. Don't Start Data.
4
Change from DC power supply to function generator. The sine indicator should be illuminated. You should already notice something different happening. What is it?
Figure 12
5
Start Data. Everything may really slow down. That's OK. The magnetic field lines are really busy! From the B-field lines and field direction arrows, we can see that the field is changing rhythmically in magnitude and direction. That makes for very large changes in the solenoid's field. It will also result in large changes in flux through any coil inside the solenoid. We'll try that shortly.
6
Turn off the "B-field Lines." They keep the computer pretty busy with all that scaling.
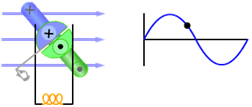
The voltage/current graph shows the sinusoidal variation in the current as shown in the top graph in Figure 14. This sinusoidal current was created by the electronics of the function generator. Normal household current varies in the same way as a natural result of using a spinning generator to produce AC current. That spinning causes the effective area of the coil to vary sinusoidally. Figure 13 is an edge-on view of a coil rotating around an axis normal to the page.
Figure 13: AC Generator
Since
Bsol = μonI,
 the corresponding magnetic field graph has a similar shape and is in sync with the current graph. Think about it. If I is varying sinusoidally, μonI will, too. That's what you see in the lower graph in Figure 14.
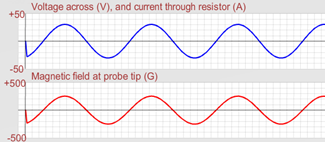
Figure 14: Effect of Current Function on Magnetic Field: Sine Function
7
Try the triangle function. The resulting graphs are shown in Figure 15.
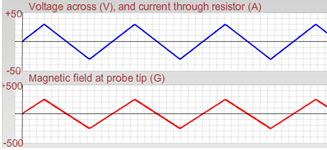
Figure 15: Effect of Current Function on Magnetic Field: Triangle Function
We'll now bring back the pickup coil and look at the emfs generated by each type of variable current.

C. Induced Emf Due to a Sinusoidal Variation in the Magnetic Field—A Qualitative Investigation

1
Adjust the DC power supply to 30.00 V.
2
Select the small pickup coil sensor and make sure it's centered.
3
Switch from DC power supply to the function generator with the sine function selected.
4
Set the Pickup EMF (V) scale to "5 mV."
5
Start Data. Let the graph fill and then Stop Data. Turn off the "Function Generator." You should get a pair of graphs similar to the ones in Figure 16. At first glance, this pair of graphs looks a lot like the previous sine function pair (Figure 14).
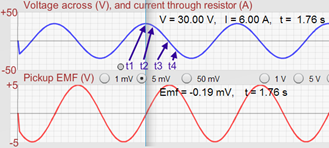
Figure 16: Sinusoidal Current and Resulting Sinusoidal Emf
The top graph is a plot of V and I vs. t in both cases. The bottom graph is a plot of the magnetic field, B vs. t in Figure 14 and emf vs. t in Figure 16.
6
What's the fundamental difference between the two pairs? (It's not the amplitude difference.)
Let's look at this in detail to see how the middle graph dictates the shift of the bottom graph. In Figure 16, the Graph Tool has been dragged to a voltage/current maximum. Note that this tool serves another purpose in this situation—to match up points created at a selected instant on each graph. Let's use this to see the meaning of the graph offset.
7
Drag your Graph Tool to the middle of a voltage peak as shown in Figure 16.
  • a
    Record t1, and I1 at that maximum current instant.
  • b
    Move to
    t2 = t1 + 0.1 s.
     Record t2, and I2. (Not +0.01, which isn't possible. It would be 1.86 s in Figure 16.)
  • c
    Calculate
    ΔI = I2 − I1.
8
Drag your Graph Tool a bit to the right to the steep part of the V, t graph where the graph crosses the time axis.
  • a
    Record t3, and I3.
  • b
    Move to
    t4 = t3 + 0.1 s.
     Record t4 and I4.
  • c
    Calculate
    ΔI = I4 − I3.
9
Which of these 0.1-s intervals involved the greater magnitude currents?
10
Which of these 0.1-s intervals involved the greater magnitude magnetic fields?
11
Which of these 0.1-s intervals involved the greater magnitude change in current?
12
Which of these 0.1-s intervals involved the greater magnitude change in magnetic field?
13
Which of these 0.1-s intervals resulted in the greater magnitude induced emf in the coil?
So when the current and field are maximum, they're changing at the slowest rate, (minimum ΔB/Δt); thus, the flux is changing less quickly. Thus, the induced emf is at its minimum, emfmin, when the current and field are maximum. And when the current and field are minimum, they're changing at the fastest rate, (maximum ΔB/Δt); thus, the flux is changing more quickly. Thus, the induced emf is the maximum, emfmax, when the current and field are minimum. Hopefully you can see now why the graphs are offset. A maximum in one corresponds to zero in the other.

D. Induced Emf Due to a Triangular Variation in the Magnetic Field—A Quantitative Investigation

1
Adjust the DC power supply to 30.00 V.
2
Select the pickup coil sensor and make sure it's centered.
3
Switch from DC Power Supply to the function generator with the triangle wave on the function generator.
4
Set the Pickup EMF (V) scale to "5 mV."
5
Start Data. Let the graph fill and then Stop Data. Whoa! Who ordered this?
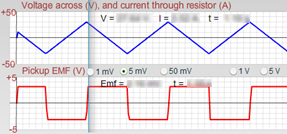
Figure 17: Sinusoidal Current and Resulting Sinusoidal Emf
How did we go from mounds to mesas? Our sinusoidal current graph in Figure 16 had a slope of zero at t1 and gradually increased in (negative) slope, reaching a maximum slope when it crossed the time axis at t3 and then began to decrease in negative slope. Thus the emf had the constantly varying value illustrated in the lower graph. Our triangular graph, in Figure 17 has a constant slope from its maximum until it crosses the time axis and for an equal time beyond. Since
B = μonI,
 we know that a graph of B vs. t has the same shape as this V, I vs. t graph. (See Figure 15.) Thus, ΔB/Δt = a constant, which is just the slope of the B, t graph during this interval. And since the pickup coil is in this region of constantly changing magnetic field, it will have a constant magnitude emf induced in it equal to
emf = −NA
ΔB
Δt
where: N = 64, the number of turns in the pickup coil, and r = 1.40 cm, the radius of the pickup coil. This emf is constant while ΔB/Δt is constant. Hence the horizontal emf lines below the straight, sloping current segments in
Figure 17. Procedure for Determining the Induced Emf in the Pickup Coil We now want to look at the emf induced in the pickup coil during a period when that emf is constant. During that period
  • a
    the pickup emf as read by the Graph Tool will be constant as indicated by the horizontal emf graph.
  • b
    the slope, ΔI /Δt, of the I vs. t graph will be constant, and as a result ΔB/Δt and the induced emf must be constant.
We'll now find both of these emf values and compare them to see if they are indeed equal. We'll do this by picking a time interval on the graphs where the emf measured on the Pickup EMF (V) graph is constant, that is where that graph is horizontal. We'll then find the slope of the I vs. t graph for that same time interval. This will allow us to calculate the emf.
6
Start Data. Let the graph fill and then Stop Data.
7
Move your Graph Tool to a position like the one shown in Figure 18, where the Graph Tool is well within the region of constant positive voltage on the Pickup EMF (V) graph. Record that constant emf value as emfmeasured. This is the emf produced in the coil.
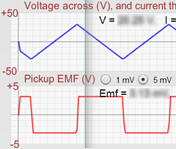
Figure 18: Constant Emf with Constant ΔI/Δt
8
Using the Graph Tool find t1 and t2, the beginning and ending times of the constant emf period. Record these times in Table 2. (These instants are referred to as Points 1 and 2 in Table 2.)
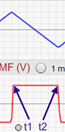
Figure 19
9
Similarly find I1 and I2, the currents at t1, and t2. Do this by moving the Graph Tool to each of these times and then read the current from the middle graph. The Graph Tool actually displays these currents for you. Record these in Table 2. Be sure to include the signs.
10
Calculate the magnetic field at the center of the solenoid for each current using
B = μonI.
 Record these values in Table 2.
11
Calculate the theoretical emf from equation 4
emf = −NA
ΔB
Δt
.
. You'll need N and the radius for the coil provided in Part IID. Record this value.
12
Calculate the percentage error between the theoretical and measured values for the emf.
If it's more than a few percent (5%), you probably need to retake your data or ask for help.

E. Maximizing the Emf

You've now learned how to calculate the induced emf in the mathematically simple case of a triangle-shaped current vs. time relationship. Let's consider how we might increase the emf of our simple generator. Faraday's Law suggests four changes that we might try.
( 6 )
emf = −N
Δ(BA)
Δt
We could
  • •
    increase the solenoid field, B, by increasing the current.
  • •
    increase the cross-sectional area, A of the pickup coil.
  • •
    decrease the time, Δt, for a given change in B.
  • •
    increase the number of loops on the pickup coil, N
Let's try the last two. Decreasing Δt—the Effect of Frequency on Induced Emf
The time for one complete cycle, the period, T, is the time between two peaks on the V, t graph.
If you reduced this interval, that is reduced the time for a cycle, the straight segments would be steeper. Thus, Δt for a cycle would be smaller, making ΔB/Δt larger, resulting in a larger induced emf. Halving the period would double the emf, etc. Our apparatus provides a way to increase the frequency. Since the frequency is the inverse of the period,
f = 1/T,
 halving the period is accomplished by doubling the frequency. Let's try that.
Figure 17: (repeated)
Frequency f1 Beside the function generator are four radio buttons for selecting the frequency. We've been using the base frequency, f1.
1
If you don't still have Figure 17 on your screen, create a new one.
2
Record your emfmeasured for frequency f1 (from Part IID).
3
Find the period, T1, corresponding to the base frequency, f1. For best accuracy measure the time for four complete cycles, then calculate the time for one cycle. The inverse of this value is the base frequency, f1. Record the values in Table 3. Show your calculations for T1 and f1.
Frequency f2
4
Select f2 from the frequency selector.
5
Start Data. Whoops! You're going to need to change the Pickup (V) EMF graph scale. It returns the maximum possible reading of
5.0 mV,
 in this case, for readings that are "off the scale" but the actual value is somewhat higher. In retrospect this shouldn't be a surprise. Our goal was to increase the emf. Increase the Pickup EMF (V) scale to "50 mV" and try again.
6
Record emfmeasured for frequency f2.
7
Just as before, find the period, T2, and the frequency f2. Show your calculations for T2 and f2.
8
Also calculate the ratio f2/f1.
9
The ratio f2/f1 should equal approximately 2.0. How does the emf generated using the frequency f2 compare to the emf generated using a frequency f1?
10
Try this. Leave the Pickup EMF (V) voltage scale at "50 mV." Return the frequency to f1 and Start Data. While the graph is being drawn, change the frequency to f2. Note the typical values for the maximum current in the solenoid for f1, and for f2. You won't get exactly the same current values at each maximum because the current is changing very rapidly and the Graph Tool doesn't record current values frequently enough to catch the current at every instant. This would be true with any instrument. But it should be clear that the frequency has had no effect on the maximum + and – currents.
11
What has changed in the f2 section of the voltage, current graph as a result of doubling the frequency?
12
Explain why this should affect the induced emf. And specifically explain why the emf doubled when the frequency doubled. Remember that
emf = −NA
ΔB
Δt
 and
B = μonI.
Household electricity in many countries is produced at 60 Hz, which is more than 30 times larger than what we're using in this lab. You can see how that would be an advantage.
Effect of the Number of Turns, N, on the Pickup Coil on the Induced Emf The magnetic field of the solenoid does work on the electrons in the pickup coil. This work/charge is the induced emf. So you might say that the coil is somewhat like a battery where charges are pushed by electromagnetic forces from one end of the battery to the other, thus increasing their energy. When two batteries are connected in series, the energy acquired by the charges is double the amount of one single battery. A similar effect occurs when the number of loops is increased. The more loops the charges are pushed through, the more energy they acquire, or the more work is done to them. Let's confirm this relationship by taking a new set of data. We'll switch to a coil that has twice the number of coils (128). You'll have to reset its position so that its center is at about 0 m.
1
Select Pickup coil (double).
2
Carefully set the coils' separation to 0 m using the Coil Separation (m) graph as before.
3
While we're at it, let's go for the maximum emf that we can produce with this apparatus. So set the frequency to the highest value, f4.
4
Record your original measured emf for Part IIE.
5
What do you predict for your new emf with N = 128 and f = f4? Explain your reasoning.
6
Start Data and let the screen fill with plotted data.
7
Record your measured emf for f4 and N = 128.
Hopefully you found that the emf was multiplied by a factor of approximately eight. If not, try again.

Copyright © 2013-2014 Advanced Instructional Systems, Inc. and Kentucky Educational Television | Credits