To make exact eclipse predictions, you would need to calculate the precise motions of the sun and moon, and that requires a computer and proper software. Such software is available for desktop computers, but it isn’t necessary if you are satisfied with making less exact predictions. In fact, many primitive peoples, such as the builders of Stonehenge and the ancient Maya, are believed to have made eclipse predictions.

You should think about eclipse prediction for three reasons. First, it is an important part of the history of science. Second, it illustrates how apparently complex phenomena can be analyzed in terms of cycles. Third, eclipse prediction will exercise your mental muscles and force you to see Earth, the moon, and the sun as objects moving through space.

Conditions for an Eclipse

You can predict eclipses by understanding the conditions that make them possible. As you begin to think about these conditions, be sure you are aware of your point of view. (See Window on Science 3-1.) Later you will change your point of view, but to begin you must imagine that you can look up into the sky from your home on Earth and see the sun moving along the ecliptic and the moon moving along its orbit.

The orbit of the moon is tipped 5°8'43" to the plane of Earth’s orbit, so you see the moon follow a path tipped by that angle to the ecliptic. Each month, the moon crosses the ecliptic at two points called nodes. It crosses at one node going southward, and two weeks later it crosses at the other node going northward.

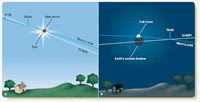
Eclipses can only occur when the sun is near one of the nodes of the moon’s orbit. A solar eclipse happens at new moon if the moon passes in front of the sun. Most new moons pass too far north or too far south of the sun to cause an eclipse. Only when the sun is near a node in the moon’s orbit can the moon cross in front of the sun, as shown in Figure 3-12a. A lunar eclipse doesn’t happen at every full moon because most full moons pass too far north or too far south of the ecliptic and miss Earth’s shadow. The moon can enter Earth’s shadow only when the shadow is near a node in the moon’s orbit, and that means the sun must be near the other node. This is shown in Figure 3-12b.

So there are two conditions for an eclipse: The sun must be crossing a node, and the moon must be crossing either the same node (solar eclipse) or the other node (lunar eclipse). That means, of course, that solar eclipses can occur only when the moon is new, and lunar eclipses can occur only when the moon is full.

Now you know the secret of predicting eclipses. An eclipse can only occur during a period called an eclipse season during which the sun is close to a node in the moon’s orbit. For solar eclipses, an eclipse season is about 32 days long. Any new moon during this period will produce a solar eclipse. For lunar eclipses, the eclipse season is a bit shorter, about 22 days. Any full moon in this period will encounter Earth’s shadow and be eclipsed.

This makes eclipse prediction easy. All you have to do is keep track of where the moon crosses the ecliptic (where the nodes of its orbit are). When the sun is near one of these nodes, you can predict that the nearest new moon will cause a solar eclipse and the nearest full moon will cause a lunar eclipse. This system works fairly well, and ancient astronomers such as the Maya may have used such a system. You could be a very successful ancient Mayan astronomer with what you know about eclipse seasons, but you can do even better if you change your point of view.

The View from Space

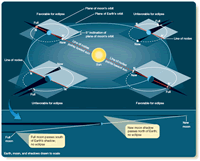
Change your point of view and imagine that you are looking at the orbits of Earth and the moon from a point far away in space. You would see the moon’s orbit as a small disk tipped at an angle to the larger disk of Earth’s orbit. As Earth orbits the sun, the moon’s orbit remains fixed in direction. The nodes of the moon’s orbit are the points where it passes through the plane of Earth’s orbit; an eclipse season occurs each time the line connecting these nodes, the line of nodes, points toward the sun. Study Figure 3-13 and notice that the line of nodes does not point at the sun in the example at lower left, and no eclipses are possible. At lower right, the line of nodes points toward the sun, and the shadows produce eclipses.

The shadows of Earth and moon, seen from space, are very long and thin, as shown in the lower part of Figure 3-13. It is easy for them to miss their mark at new moon or full moon and fail to produce an eclipse. Only during an eclipse season, when the line of nodes points toward the sun, do the long, skinny shadows produce eclipses.

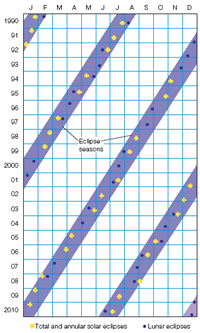
If you watched for years from your point of view in space, you would see the orbit of the moon precess like a hubcap spinning on the ground. This precession is caused mostly by the gravitational influence of the sun, and it makes the line of nodes rotate once every 18.6 years. People back on Earth see the nodes slipping westward along the ecliptic 19.4° per year, and the sun takes only 346.62 days (an eclipse year) to return to a node. This means that, according to the calendar, the eclipse seasons begin about 19 days earlier every year (Figure 3-14).

The cyclic pattern of eclipses shown in Figure 3-14 should give you another clue how to predict eclipses. Eclipses follow a pattern, and if you were an ancient astronomer and understood the pattern, you could predict eclipses without ever knowing what the moon was or how an orbit works. All you need know is the cycle.

The Saros Cycle

Ancient astronomers could predict eclipses in a crude way using the eclipse seasons, but they could have been much more accurate if they recognized that eclipses occur following certain patterns. The most important of these is the saros cycle (sometimes referred to simply as the saros). After one saros cycle of 18 years 11⅓ days, the pattern of eclipses repeats. In fact, saros comes from a Greek word that means “repetition.”

The eclipses repeat because, after one saros cycle, the moon and the nodes of its orbit return to the same place with respect to the sun. One saros contains 6585.321 days, which is equal to 223 lunar months. Therefore, after one saros cycle the moon is back to the same phase it had when the cycle began. But one saros is also equal to 19 eclipse years. After one saros cycle, the sun has returned to the same place it occupied with respect to the nodes of the moon’s orbit when the cycle began. If an eclipse occurs on a given day, then 18 years 11⅓ days later the sun, the moon, and the nodes of the moon’s orbit return to nearly the same relationship, and the eclipse occurs all over again.

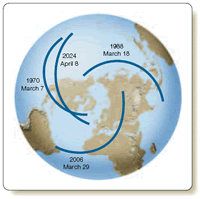
Although the eclipse repeats almost exactly, it is not visible from the same place on Earth. The saros cycle is one-third of a day longer than 18 years 11 days. When the eclipse happens again, Earth will have rotated one-third of a turn farther east, and the eclipse will occur one-third of the way westward around Earth (Figure 3-15). That means that after three saros cycles—a period of 54 years 1 month—the same eclipse occurs in the same part of Earth.

One of the most famous predictors of eclipses was the Greek philospher Thales of Miletus (about 640–546 BC), who supposedly learned of the saros cycle from the Chaldeans, who had discovered it. No one knows which eclipse Thales predicted, but some scholars suspect the eclipse of May 28, 585 BC. In any case, the eclipse occurred at the height of a battle between the Lydians and the Medes, and the mysterious darkness in midafternoon so startled the two factions that they concluded a truce.

In fact, many historians doubt that Thales actually predicted the eclipse. It would have been very difficult to gather enough information about past eclipses; total solar eclipses are rare as seen from any one place. If you stay in one city, you will see a total solar eclipse about once in 360 years. Also, 585 BC is very early for the Greeks to have known of the saros cycle. The important point is not that Thales did it, but that he could have done it. If he had had records of past eclipses of the sun visible from the area, he could have discovered that they tended to recur with a period of 54 years 1 month (three saros cycles). Indeed, he could have predicted the eclipse without ever understanding what the sun and moon were or how they moved.

Why can’t two successive full moons be totally eclipsed?
Most people suppose that eclipses occur at random or in some pattern so complex you need a big computer to make predictions. You know the geometry is fairly simple, so you can build a simple argument to analyze this question. Remember that a total lunar eclipse occurs when the moon passes through Earth’s shadow. Earth’s shadow always points toward the ecliptic exactly opposite the sun, and most of the time the moon will pass north or south of Earth’s shadow, and there will be no eclipse. A lunar eclipse can happen only when the sun is near one node and the moon crosses Earth’s shadow at the other node.

Now you can apply what you know about the moon’s phases. An eclipse season for a total lunar eclipse is only 22 days long, but the moon takes 29.5 days to go from one full moon to the next. If one full moon is totally eclipsed, the next full moon 29.5 days later will occur long after the end of the eclipse season and there will be no eclipse.

Now use your knowledge of the cycles of the sun and moon to revise your argument. Why can the sun be eclipsed by two successive new moons?

Connections: Predicting eclipses isn’t very hard, and many ancient peoples were probably familiar enough with the cycles of the sun and moon to know when eclipses were likely. Some people call those first predictions early science, but science involves understanding nature, not just predicting events. In the next chapter, you will see how modern science was born when astronomers tried to understand the cycles they saw in the sky.

Click image to enlarge

Figure 3-12
Eclipses can occur only near the nodes of the moon’s orbit. (a) A solar eclipse occurs when the moon meets the sun near a node. (b) A lunar eclipse occurs when the sun and moon are near opposite nodes. Partial eclipses are shown here for clarity.

Click image to enlarge

Figure 3-13
The moon’s orbit is tipped about 5° to Earth’s orbit. The nodes N and N’ are the points where the moon passes through the plane of Earth’s orbit. If the line of nodes does not point at the sun, the long narrow shadows miss, and there are no eclipses at new moon and full moon. At those parts of Earth’s orbit where the line of nodes points toward the sun, eclipses are possible at new moon and full moon.

Click image to enlarge

Figure 3-14
A calendar of eclipse seasons. Each year the eclipse seasons begin about 19 days earlier. Any new moon or full moon that occurs during an eclipse season results in an eclipse. Only total and annular eclipses are shown here.

Click image to enlarge

Figure 3-15
The saros cycle at work. The total solar eclipse of March 7, 1970, recurred after 18 years 11⅓ days over the Pacific Ocean. After another interval of 18 years 11⅓ days, the same eclipse was visible from Asia and Africa. After a similar interval, the eclipse will again be visible from the United States.