Significant Figures

Significant Figures In Calculations

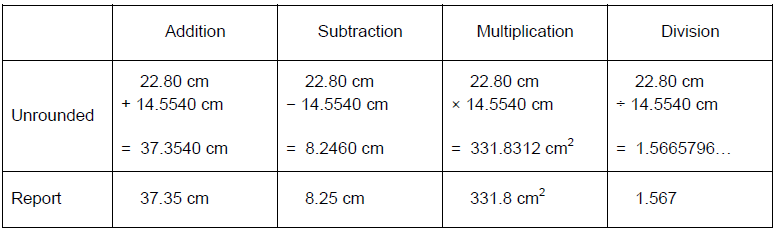
Values cannot become more precise by mathematical manipulation. The following are purely mathematical rules for significant figures in the absence of experimental limitations on precision. Addition and subtraction

•
The final answer is rounded to the least precise decimal place.

Multiplication and division

•
The final answer is rounded to the least number of significant figures.

Two lengths, 22.80 cm and 14.5540 cm, are mathematically combined in the four basic ways (+, –, ×, ÷).

Significant Figures In Experiments

A measured quantity is usually reported as the value and its associated uncertainty. In this class, the following generic symbols are used: x for the value, <x> for the average, and σ for the uncertainty or standard deviation. Please note that uncertainty and standard deviation are technically not the same, but this idea will be covered in more advanced classes. For a single measurement of one quantity, the uncertainty is generally determined by the instrument used.

The pan balance reads to 0.01 g, so an example data would be: 25.10 ± 0.01 g.
The analytical balance reads to 0.0001 g, so an example would be: 25.1000 ± 0.0001 g.
A 100-mL graduated cylinder might read to 0.5 mL, so examples are: 25.0 ± 0.5 mL or 31.0 ± 0.5 mL.

For multiple measurements of the same quantity, generally the average value is determined. The uncertainty (or standard deviation) can be calculated based on the random fluctuation of the individual data points around the average. For n measurements of x:

( 1a )

<x> =

(x₁ + x₂ +

+ x_n)

and

( 1b )

σ ≡

(x₁ − <x>)² + (x₂ − <x>)² +

+ (x_n − <x>)²

n − 1

Mathematical Manipulations Of Data And Error Propagation

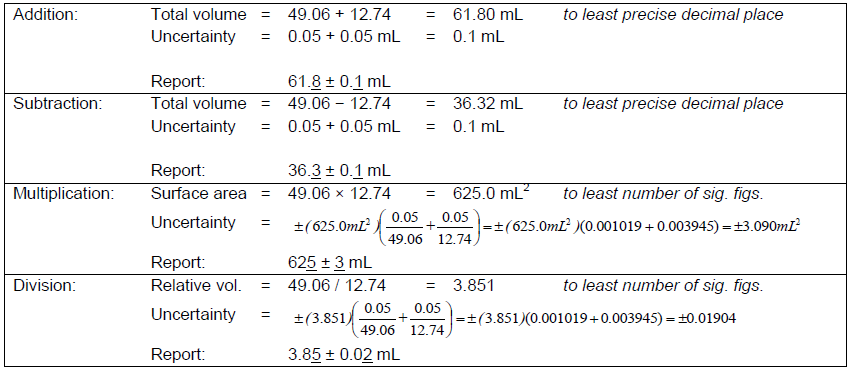
For calculations involving the addition, subtraction, multiplication, and division of two numbers, A ± σ_a and B ± σ_a, the following conventions are followed. Addition and subtraction—uncertainties add.

( 2 )

Addition: (A ± σ_a) + (B ± σ_b) = (A + B) ± (σ_a + σ_b)

( 3 )

Subtraction: (A ± σ_a) − (B ± σ_b) = (A − B) ± (σ_a + σ_b)

Multiplication and division—use relative errors.

( 4 )

Multiplication: (A ± σ_a)(B ± σ_b) = (AB) ± (AB)

σ_a

σ_b

( 5 )

Division:

(A ± σ_a)

(B ± σ_b)

σ_a

σ_b

Relative errors in A and B are the following.

( 6 )

σ_a

and

σ_b

Percent errors in A and B are the following.

( 7 )

σ_a

× 100% and

σ_b

× 100%

Uncertainty values should contain one significant figure. Final values are reported to that same decimal place. For example, suppose two volumes are determined: 49.06 ± 0.05 mL and 12.74 ± 0.05 mL.