Lab 3 - Heats of Transition, Heats of Reaction, Specific Heats, and Hess's Law
Goal and Overview
A simple calorimeter will be made and calibrated. It will be used to determine the heat of fusion of ice, the specific heat of metals, and the heat of several chemical reactions. These heats of reaction will be used with Hess's law to determine another desired heat of reaction.Objectives of the Data Analysis
-
•understand calorimetry and the concepts and uses of heat transfer
-
•understand heat transfer processes
-
•understand a variety of heat-related topics, including specific heat and heat capacity, heat of fusion, and heat of a chemical reaction
-
•use Hess's Law to deduce an unknown heat of reaction
Suggested Review and External Reading
-
•See reference section; textbook information on calorimetry and thermochemistry
Background
The internal energy, E, of a system is not always a convenient property to work with when studying processes occurring at constant pressure. This would include many biological processes and chemical reactions done in lab. A more convenient property is the sum of the internal energy and pressure-volume work(−wsys = PΔV
at constant P). This is called the enthalpy of the system and is given the symbol H.
( 1 )
H ≡ E + pV (definition of enthalpy, H)
( 2 )
ΔH ≡ Hfinal − Hinitial = qp = heat absorbed by system (constant p)
-
1Thermal Enthalpy. The higher the system's temperature, the greater its enthalpy. This makes sense because it takes heat to raise the temperature of an object.
-
2Phase Enthalpy. The liquid phase has higher enthalpy than the solid, and the vapor phase has higher enthalpy than the liquid. This also makes sense because it takes heat to melt a solid or to vaporize a liquid.
-
3Chemical Enthalpy. Chemical bonds store energy. When a chemical reaction occurs, the chemical enthalpy of the reactants changes when they form products.
-
iIf the reaction is exothermic, the chemical enthalpy decreases as the reaction proceeds.
-
iiIf the reaction is endothermic, the chemical enthalpy increases as the reaction proceeds.
-
ΔH ≡ Hfinal − Hinitial = qp = heat absorbed by system (constant p)
Temperature
When there is a change in the temperature of the system, ΔH is proportional to the temperature change,Tfinal − Tinitial = ΔT.
The proportionality constant is called the heat capacity, and is given the symbol C.
( 3 )
ΔH ≡ Hfinal − Hinitial = C(Tfinal − Tinitial) = CΔT (temperature change)
( 4a )
Ctotal ≡ m cper gram = n Cper mole
( 4b )
ΔH = Ctotal ΔT = m cper gram ΔT = n Cper mole ΔT
| c: | energy per gram per degree | e.g., J/°C · g |
| C: | energy per mole per degree | e.g., J/°C · mol |
| Cgeneral | energy per degree | e.g., J/°C. |
Phase
At a phase change, the temperature of the system is constant until the transition is complete. The amount of heat required is proportional to the amount or material present, and the ΔH of the phase transition. The heat energy can also be expressed in terms of moles (heat per mole).( 5 )
ΔH = m Δhper gram = n ΔHper mole (phase change)
Chemical Reaction
The chemical reactions studied here occur at a particular pressure and temperature. Each reaction has an associated enthalpy change that is called the heat or enthalpy of reaction that depends on the way the reaction is balanced. For example,ΔHreaction
for 2 H2O → 2 H2 + O2
is twice that forH2O → H2 + 1/2 O2, and ΔHreaction
is the heat absorbed when 2 moles of water decompose to give two moles of hydrogen and one mole of oxygen. In general, the equation to calculate the heat change is similar to Eq. 5ΔH = m Δhper gram = n ΔHper mole (phase change)
.
( 6 )
ΔH = m Δhper gram = n ΔHper mole (reaction)
Calorimeter
A calorimeter is an insulated vessel in which physical or chemical processes are performed while neglecting heat flow between the vessel and its surroundings. A process in which the heat flow, q, equals zero is called adiabatic. To a first approximation, the heat flow (+ or –) between calorimeter and the surroundings is zero, so ΔH (or q) for the calorimeter and its contents will be zero.( 7 )
ΔHcalorimeter and contents = qtotal = 0 (master equation for calorimeters)
Example 1: Calorimeter Calibration
A mass m1 of water at temperature T1 is placed in the calorimeter. Mass m2 of water at T2 is added. The calorimeter itself has a small heat capacity that must be accounted for in order to have reasonable precision. The calorimeter always contributes a term to the total enthalpy change.( 8 )
ΔHcalorimeter = Ccalorimeter(Tfinal − Tinitial contents)
( 9a )
ΔHtotal = 0
( 9b )
ΔH1 + ΔHcalorimeter + ΔH2 = 0
( 9c )
m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2cwater(Tfinal − T2) = 0
ΔH = m Δhper gram = n ΔHper mole (phase change)
was used for ΔH1
and ΔH2. Generally all but one quantity in calculations like that shown in Eqns 9aΔHtotal = 0
, 9bΔH1 + ΔHcalorimeter + ΔH2 = 0
, and 9c m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2cwater(Tfinal − T2) = 0
are measured or known. The equation is then solved for
the unknown value.
Example 2: Specific Heat Determination
Suppose a mass m1 of water with specific heat c1 is placed in the calorimeter at T1. Then a mass m2 of another substance, such as a metal, at T2 and with specific heat c2 is added. The equation is similar to that of Eqns 9aΔHtotal = 0
, 9bΔH1 + ΔHcalorimeter + ΔH2 = 0
, and 9c m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2cwater(Tfinal − T2) = 0
except that the 'c's do not cancel in the last
step.
( 10a )
ΔHtotal = 0
( 10b )
ΔH1 + ΔHcalorimeter + ΔH2 = 0
( 10c )
m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2c2(Tfinal − T2) = 0
ΔH = m Δhper gram = n ΔHper mole (phase change)
was used for ΔH1 and ΔH2. Again, usually all but one quantity are measured or known. The equation is then solved for the unknown value.
In 1819, after analyzing the heat capacities of many solid elements, Dulong and Petit proposed this generalization known as the Law of Dulong and Petit:
( 11 )
| Cper mole = MM cper gram = constant for all metals = 3R |
| MM = molar mass of the metal; R = gas constant (8.314 J/k · mol). |
Example 3: Enthalpy of Phase Change Determination
Suppose a mass m1 of water is placed in the calorimeter at T1, and mass m2 of ice at 0°C is added. As the apparatus reaches thermal equilibrium, several things occur. First, the ice melts, pulling its heat of fusion out of the thermal energy of the water and calorimeter, thus lowering their temperatures. Second, when the ice has melted, the resulting liquid is still at 0°C, so that water has to be further heated until it, the water it is cooling, and the calorimeter reach the same final temperature.( 12a )
ΔHtotal = 0
( 12b )
ΔHcool water + ΔHcool calorimeter + ΔHmelt ice + ΔHwarm melted ice = 0
( 12c )
| m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + mice Δhfusion, per g + |
| miceCwater(Tfinal − 0°C) = 0 |
Example 4: Reaction Enthalpy Determinations
Suppose mass m1 of a water-based solution is placed in the calorimeter at T1. To that mass m2 of a substance of molar mass M2 is added and it reacts with the solution. If substance 2 is the limiting reactant, then all of it will react. The enthalpy change will depend on the heat of reaction and on the number of moles of substance 2 added, n2 = m2/MM2. In this case, there are three contributions to the total enthalpy change of zero. They are due to the temperature change of the water solution and calorimeter, plus the enthalpy change due to the chemical reaction. For reactions in solution, the heat capacities of the reactants and products are approximated as zero because only the water and the calorimeter have significant heat capacity. In the last step it is assumed that the chemical reaction is written in such a way that the stoichiometric coefficient on the reactant, substance 2, is 1.( 13a )
ΔHtotal = 0
( 13b )
ΔH1 + ΔHcalorimeter + ΔHchemical reaction = 0
( 13c )
m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) +
ΔHreaction = 0
| m2 |
| MM2 |
Experimental Notes
There are two possibilities for your calorimeter setup, but both require the same procedure.-
aCoffee Cup Calorimeter Setup — the calorimeter consists of two nested Styrofoam cups with a lid.
-
bStyrofoam Calorimeter Setup — the calorimeter consists of a Styrofoam base and lid.
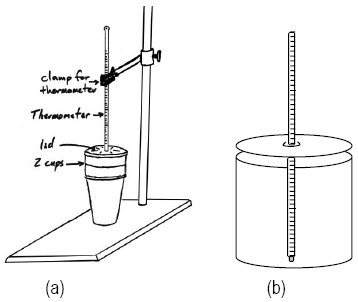
Figure 1
Please do not throw your calorimeter away. Return it clean to the reagent bench. this applies to both (a) and (b).
Measurements
The two key measurements for all calorimetry experiments are masses and temperature changes. Make sure you have all of the data you need to complete the lab. You may need these conversion factors: 1000 J = 1 kJ, and 4.184 J = 1 cal.
Note: Make sure you record/obtain all information required to complete the calculations. This includes the heat capacity of all calorimeters used to gather your data.
Procedure
Part 1: Heat Capacity of the Calorimeter
This is the experiment discussed in Example 1. This result is important because you will use it in the other experiments you perform with this calorimeter.1
Record the mass of your calorimeter to 0.01 g.
2
Add about 100 mL of room temperature water.
3
Record the mass of the calorimeter and water; determine the mass of this water by difference to 0.01 g.
4
To equilibrate the beaker used to transfer the warm water to the calorimeter, take a small beaker to one of the warm water baths (approximately 35°C) in the lab. Submerge the beaker in the warm water bath for a couple minutes.
5
Record the temperature (to the nearest 0.1°C) of the water in both the warm water bath and in your calorimeter just before you add the warm water to the room temperature water.
6
Make sure your calorimeter is at least 4 feet away from any hot plate, and try to minimize drafts.
7
Using the equilibrated beaker, scoop up about 100 mL of warm water from the water bath and pour it into your calorimeter.
8
Quickly put on the lid and insert the thermometer.
9
Stir the water and read the final temperature reached by the mixture to 0.1°C.
10
Remove the thermometer and record the final mass (so you can determine the mass of warm water added) to 0.01 g.
11
Redo the calibration at least one time to verify the calorimeter's heat capacity.
12
Calculate the heat capacity of your calorimeter, using Eqns. 9aΔHtotal = 0
, 9bΔH1 + ΔHcalorimeter + ΔH2 = 0
, and 9c m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2cwater(Tfinal − T2) = 0
.
( 9d )
| ΔH1 + ΔHcalorimeter + ΔH2 = |
| m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2c2(Tfinal − T2) = 0 |
-
Finding the heat capacity of your calorimeter this way is very sensitive to small errors. The "correct" value is probably between 5 and 150 J/°C. If you get a negative value or a very large value, re-do the calculation or the experiment. Use a new set of cups if you get a high calorimeter constant (heat loss).
Part 2: Heat of Fusion of Ice
This is the experiment discussed in Example 3.1
Record the mass of your empty, dry calorimeter to 0.01 g.
2
Add about 100 mL of room temperature water.
3
Record the mass of the calorimeter and water; determine the mass of this water by difference to 0.01 g.
4
Place your calorimeter on a ring stand and carefully clamp your thermometer (inserted through a slotted rubber stopper) to the stand so that the thermometer nearly reaches the bottom of the calorimeter.
5
Measure the temperature of your water to 0.1°C.
6
Add about 25 g of ice. Solid ice is preferred over slushy ice. Why is this?
7
Swirl the calorimeter to enhance mixing and watch as the temperature falls.
8
Record the lowest temperature reached to 0.1°C.
9
Carefully remove the thermometer and record the final mass to 0.01 g (so you can determine the mass of ice added).
10
Calculate the heat of fusion of ice in J/g, using Eqns. 12aΔHtotal = 0
, 12bΔHcool water + ΔHcool calorimeter + ΔHmelt ice + ΔHwarm melted ice = 0
, and 12c.
( 12d )
| ΔHcool water + ΔHcool calorimeter + |
| ΔHmelt ice + ΔHwarmup melted ice = m1cwater(Tfinal − T1) + |
| Ccalorimeter(Tfinal − T1) + mice Δ hfusion, per g + mice cwater(Tfinal − 0°C) = 0 |
11
Some liquid water probably went into your calorimeter along with the ice. How would that affect your result?
12
Convert your answer into units of kJ/mol. Report your answer to three significant figures.
13
Calculate the percent error in your experimental result relative to the literature value of 6.01 kJ/mol.
Part 3: Specific Heat of a Metal
Begin the temperature equilibration of the metal at the beginning of the lab. This is the experiment given in Example 2.1
You will study either copper or aluminum. Record which metal you choose.
2
Take 20–30 g of the metal and record the mass to 0.01 g.
3
Carefully place the metal in a large test tube suspended in a boiling water bath made in a 400 mL beaker.
4
Leave the test tube there for at least 30 minutes to equilibrate the metal to the temperature of the bath. Do this at the start of the experiment so the metal heats while you are doing other things. Keep the calorimeter away from the hot plates.
Caution:
Steam burns are especially severe, as the steam condenses to liquid on your skin and gives up its heat of vaporization to the tissues. So whenever you work around steam, pay attention.
Steam burns are especially severe, as the steam condenses to liquid on your skin and gives up its heat of vaporization to the tissues. So whenever you work around steam, pay attention.
5
Record the mass of the clean, dry calorimeter to 0.01 g.
6
Put about 100 mL of water into it and record the mass to 0.01g.
7
Record the temperature of the water and calorimeter to 0.1°C.
8
Carefully record the temperature of the "boiling" water bath with a 110°C thermometer (to 0.5°C).
9
Carefully slide the hot metal from the test tube into the calorimeter. Do not hit the thermometer or add boiling water from the bath. Do not let the thermometer touch the metal.
10
Swirl the calorimeter gently and constantly.
11
Record the maximum temperature to 0.1°C.
12
Return the clean, dry, cool metal to the reagent bench.
13
Calculate the specific heat of your metal to three significant figures, using Eqns. 10aΔHtotal = 0
, 10bΔH1 + ΔHcalorimeter + ΔH2 = 0
, and 10cm1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2c2(Tfinal − T2) = 0
, in units of J/g and J/mol.
( 10d )
| ΔH1 + ΔHcalorimeter + ΔH2 = |
| m1 cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) + m2 c2(Tfinal − T2) = 0 |
14
Using the molar mass and experimental specific heat of your metal, calculate the molar heat capacity, C, and compare it to the Dulong and Petit value of 3R (R = 8.314 J/K · mol).
Part 4: Heat of a Chemical Reaction
This experiment is discussed in Example 4. You will measure the heats of two reactions:-
aMg + 2 HCl → MgCl2 + H2(g) ΔHa = measured
-
bMgO + 2 HCl → MgCl2 + H2O(l) ΔHb = measured
-
cH2(g) + 1/2 O2(g) → H2O(l) ΔHc = −285.8 kJ
-
dMg + 1/2 O2 → MgO ΔHd = ???
1
Record the mass of the clean, dry calorimeter to 0.01 g.
2
Put 50 mL of distilled water into the calorimeter.
3
Add 25 mL of approximately 2 M HCl.
4
Record the mass of this water and acid combination to 0.01 g.
5
Take about 0.10–0.15 g of magnesium ribbon and record its mass to 0.01 g.
6
Take the initial temperature of the acidic water in the calorimeter to 0.1°C.
7
Add the metal, stir constantly, and record the maximum temperature reached to 0.1°C. The reaction takes a while, so be patient.
8
Repeat this procedure substituting about 0.30g of magnesium oxide for the magnesium ribbon.
The goal is to determine the heat of reaction for the combustion of magnesium to form the oxide.
Target:
Target:
Mg + 1/2 O2 → MgO ΔHrxn = ?
9
Using Eqns. 13aΔHtotal = 0
, 13bΔH1 + ΔHcalorimeter + ΔHchemical reaction = 0
, and 13cm1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) +
ΔHreaction = 0
, calculate the experimental values of | m2 |
| MM2 |
ΔHa and ΔHb
reactions (a) and (b) to three significant figures.
( 13d )
| ΔH1 + ΔHcalorimeter + ΔHchemical reaction = | ||
m1cwater(Tfinal − T1) + Ccalorimeter(Tfinal − T1) +
|
10
Using ΔHa, ΔHb, and ΔHc , employ Hess' Law to calculate the heat of reaction for the magnesium combustion reaction (to three significant figures).
Note: Whenever you reverse a reaction, the sign of ΔH changes. That is because enthalpy is a state function; ΔH of state 2 to state 1 is equal in magnitude but opposite in sign of ΔH from state 1 to state 2.
11
Calculate the percent error in experimental value for the target reaction (literature value for the heat of formation of MgO(s) –601 kJ) to three significant figures.
12
Calculate the percent error in your experimental ΔHa and ΔHb values (literature values are –462 kJ/mol for (a) and –146 kJ/mol for (b)) to three significant figures.
Reporting Results
Complete your lab summary or write a report (as instructed).Abstract
Results (final results are reported to three significant figures)
-
Calorimeter heat capacity
-
Heat of fusion of ice
-
Specific heats of metals
-
Heats of reaction from part 4 and for combustion of Mg.
Sample Calculations
-
Calorimeter heat capacity (part 1)
-
Heat of fusion of ice (part 2)
-
Specific heat of metals (part 3)
-
Heat of reaction for one of part 4 reactions (part 4)
-
Heat of magnesium combustion using Hess' Law (part 4)
Discussion
-
What you found out and how for each part
-
How good was your data (comparison to expected values, etc.)
-
Ideas to improve the accuracy in any or all of the procedures utilized in this experiment?
-
What conclusions can you draw?
