Lab 11 - Spectroscopic Determination of an Equilibrium Constant
Goal and Overview
The reaction of iron (III) with thiocyanate to yield the colored product, iron (III) thiocyanate, can be described by the following equilibrium expression.( 1 )
Fe3+ + SCN− 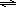 FeSCN2+
FeSCN2+
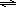 FeSCN2+
FeSCN2+ Keq,
the equilibrium constant for the reaction.
Objectives of the data analysis
-
•use Beer's Law to characterize amounts of molecules
-
•calculate solution concentrations resulting from volumetric dilutions
-
•understand equilibrium principles and manipulate equilibrium constant expressions
-
•determine equilibrium concentrations and equilibrium constants
-
•consider the effects of error when assumptions are used
Suggested review and external reading
-
•Reference information on spectroscopy (see Lab 9) and dilutions; relevant textbook information on spectroscopy and equilibrium
Background
This experiment investigates the equilibrium established by the reaction of the iron (III), Fe3+, and the thiocyanate, SCN–, ions. See Eq. 1Fe3+ + SCN− 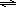 FeSCN2+
FeSCN2+
. The reactants are colorless, but the FeSCN2+ ion is orange-red colored. At equilibrium, the concentrations of these three ions must be related to each other according to the equilibrium constant expression.
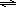 FeSCN2+
FeSCN2+ ( 2 )
K =
| [FeSCN2+] |
| [Fe3+][SCN−] |
( 3 )
A = −log(T) = εbc
( 4 )
T =
= 10−εbc = 10−A
| %T |
| 100% |
K =
allows the equilibrium constant for this reaction to be calculated.
| [FeSCN2+] |
| [Fe3+][SCN−] |
Procedure
Part 1: Qualitative Observations: Is the reaction exothermic or endothermic?
1
Using a 10 mL graduated cylinder, measure out approximately 2 mL of 2 × 10–3 M NaNO3 and put it in a test tube.
2
Add approximately 8 mL of 2 × 10–3 M NaSCN.
3
Add approximately 10 mL of 2 × 10–3 M Fe(NO3)3. Note the color of the solution.
4
Fill a Spec 20 cuvette no more than 2/3 full, and split the remaining solution among three test tubes.
5
Place one tube in an ice bath and one in the hot water bath on the hot plate.
6
After about 10 minutes, compare them with the solution at room temperature.
7
Discuss the implications of your observations, basing your discussion on your knowledge of Le Châtelier's principle.
Do your observations imply an exothermic or endothermic reaction?
Part 2: Spectral Profile and λmax (most sensitive wavelength) of FeSCN2+
1
Measure transmittance (%T) to 0.1% of the mixtures in your cuvette in the range from 370 to 560 nm.
-
aUse a cuvette containing 2 × 10–3 M NaNO3 as a blank to set 100% transmission.
-
bCheck the %T readings at 20 nm intervals.
-
cWhen you reach the region of minimum transmittance, reduce the intervals to 10 or even to 5 nm.
2
For the wavelength of minimum %T, calculate the absorbance, A, of the solution (A = –log T) to the appropriate number of significant figures.
3
Identify the wavelength of maximum absorbance, the experimental value of λmax.
How does your
λmax
compare with your answer to Question 1 of the pre-lab assignment?
4
Set your spectrometer to λmax
for parts 3 and 4.
Part 3: Beer's Law Curve for FeSCN2+: determining ε of the product at λmax
To make solutions of known concentrations of FeSCN2+, you cannot simply dissolve a salt containing FeSCN2+ in water because the ion will dissociate in order to satisfy the equilibrium constant expression.
If Keq
were known, solutions with known initial concentrations of FeSCN2+ could be made, and algebra could be used to find equilibrium concentrations of Fe3+, SCN–, and FeSCN2+. However, K is what you are trying to find in Part 4.
In order to overcome this difficulty, you will take spectral data for a set of solutions made by mixing a very high Fe3+ concentration with extremely small SCN– concentrations. Assume that SCN– is the limiting reactant (i.e., that essentially all of it is used up to make FeSCN2+). By doing this, you can equate the equilibrium concentration of iron (III) thiocyanate, [FeSCN2+]eq
to the initial concentration of thiocyanate, [SCN−]initial.
Once you have actually determined Keq,
you must return to this assumption and verify its validity.
Note for Parts 3 & 4: You may wish to split the dilution work with your partner to save time. One person could do Part 3 while the other is doing Part 4.
1
Take about 100 mL of 0.1 M Fe3+ solution (solution B) in a small labeled beaker.
2
Make the strongest colored solution of NaSCN and Fe(NO3)3 (solution A).
-
aUsing a volumetric pipet, put 5 mL of 2 × 10–3 M NaSCN (concentration known to 1%) into a 50 mL volumetric flask.
-
bFill to the mark with solution B (above; 0.1 M Fe3+ solution).
3
Use only volumetric glassware, not graduated pipets or cylinders.
-
•You have the following volumetric pipets available: 1, 2, 5, 10 mL.
-
•You have the following volumetric flasks available: 10, 50, 100 mL.
Accurately create 10 mL volumes of the following dilutions of solution A with solution B. As each of these solutions is created, measure its %T to 0.1%.
-
aPure B for use as a blank (faint straw-colored, no colored complex); this is 0.1 M Fe(NO3)3.
-
b1 mL A into 10 mL flask, filled to mark with B
-
c3 mL A into 10 mL flask, filled to mark with B
-
d5 mL A into 10 mL flask, filled to mark with B
-
e7 mL A into 10 mL flask, filled to mark with B
-
f9 mL A into 10 mL flask, filled to mark with B
-
gPure A, the pure, most red-orange solution
4
Calculate absorbance for each solution: A = –log(%T/100%).
5
Make a Beer's Law plot of absorption versus concentration of FeSCN2+ (A vs [FeSCN2+]) for these 7 points. Use two significant figures in your concentration values and three for your absorbance values.
6
Draw the best-fit straight line to the points.
7
This best-fit line mathematically has the form of Beer's Law: A = εbc, with slope = εb and y-intercept = 0; ε = molar extinction coefficient in L/mol · cm, b = pathlength in cm, and c = concentration in mol/L. Determine the slope to the ones place.
8
Using the measured pathlength b of your cuvette (to 0.01 cm) and your slope, calculate the value of the extinction coefficient for FeSCN2+ at its λmax
to the ones place.
9
Record which Spec 20 you used so you can use the same one for Part 4.
-
•Temperature Dependence: Is the reaction exothermic or endothermic? Explain.
-
•Spectral Profile: What isλmax?
-
•Beer's Law Plot: Graph of Absorbance versus [FeSCN2+] noting ε atλmax.
Part 4: Equilibrium Constant for the Formation of FeSCN2+
In this part of the experiment, you will prepare five solutions with the same initial concentration of Fe3+ ion but different initial concentrations of SCN– ion. As you make each solution, measure its percent transmittance atλmax
(Part 2) and use your Beer's Law plot (Part 3) to establish the equilibrium FeSCN2+ concentration. From the initial concentrations of the reactants and the equilibrium concentration of the product, you can calculate the experimental value of Keq
for each of the five solutions using Eq. 2K =
.
| [FeSCN2+] |
| [Fe3+][SCN−] |
1
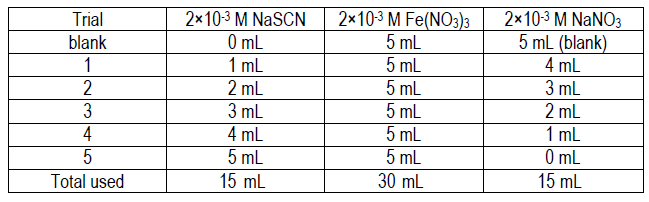
Use the solutions provided, each of which is 2 × 10–3 M: NaSCN, Fe(NO3)3, and NaNO3.
2
Use volumetric pipets and a 10 mL volumetric flask to prepare each of the following five solutions.
-
•NaSCN and Fe(NO3)3 deliver SCN– and Fe3+ to the solution.
-
•NaNO3 is used to fill the flask to 10 mL.
-
•The "Total used" row is designed to help you estimate how much of the stock solutions you should take in labeled beakers to your lab station.
-
•Please minimize waste – do not take extra and please share leftovers.
| Waste disposal: | The solutions must be put into the labeled waste bottles in the back hood. | |
| Nothing can go down the sink. | ||
| If you are ever in doubt, ask your TA. |
3
Find equilibrium concentrations of Fe3+, SCN–, and FeSCN2+ to two significant figures. (See Equations 1Fe3+ + SCN−  FeSCN2+
FeSCN2+
and 2 FeSCN2+
FeSCN2+ K =
.)
| [FeSCN2+] |
| [Fe3+][SCN−] |
ICE tables will help you determine these values. Initial amounts, changes in amounts, and final equilibrium amounts are shown. These values must be in moles/L.


-
•initial amounts of reactants (amounts before the reaction begins): determined using the dilution equation
-
•To find the initial concentration of SCN–, use the dilution equation: (M1V1)/V2 = M2, whereV2 = 10 mL.
-
•To find the initial concentration of Fe3+, use the dilution equation: (M1V1)/V2 = M2, where V2 = 10 mL.
-
-
•initial amount of product (the amount before the reaction begins): zero
-
•equilibrium concentration of product([FeSCN2+]eq):determined spectroscopically
[FeSCN2+] at equilibrium is determined using Beer's Law; x is the amount of FeSCN2+ created (determined experimentally).
( 5 )
x = [FeSCN2+]eq =
= A / slope
| A |
| εb |
-
aBegin by filling out the product column from the bottom up. Because the stoichiometry is 1:1:1, the amount of reactant consumed is equal to the amount of product formed.
-
bFill in the rest of the ICE table box-by-box until the equilibrium reactant concentrations are determined.
4
Use Eq. 2K =
and the equilibrium concentrations from the bottom row of each ICE table to calculate Keq to two significant figures for the five trials in Part 4.
| [FeSCN2+] |
| [Fe3+][SCN−] |
5
Find the average value of Keq, the standard deviation, and the relative error (standard deviation divided by the average).
Are the values of K for all trials similar? Should they be?
Assumption Check Used in Making Beer's Law Plot
Given your value of K, go back and check the validity of the assumption you made in Part 3.1
Rewrite Eq. 2K =
so that the ratio of | [FeSCN2+] |
| [Fe3+][SCN−] |
[FeSCN2+]eq
to [SCN−]eq, [FeSCN2+]eq/[SCN−]eq,
is on one side.
2
Calculate the approximate ratio of [FeSCN2+]eq/[SCN−]eq
using Keq
and [Fe3+]. Use your average value for Keq.
The Fe3+ concentration was approximately 0.1 M in Part 3; the change in its concentration should have been negligible.
3
The assumption that essentially all of the SCN– reacted to form FeSCN2+ would mean that this ratio would need to be large. Is it?
If the ratio is small, the assumption was clearly a bad one and the experiment is useless in determining the equilibrium FeSCN2+ concentration and Keq.
At least 95% of the initial SCN– should react to form FeSCN2+ at equilibrium.
4
Discuss how good the assumption was and how the assumption affected the calculated values of Keq.
-
•For example, ifKeqis 350, then[FeSCN2+]eq/[SCN−]eq ≈ 35.
-
•This means that 35 out of 36 SCN– initially present have been converted to FeSCN2+ at equilibrium; 1 out of 36 is present as SCN–.
-
•That is about a 3% error in the FeSCN2+ concentration due to just the assumption.
-
•And,[FeSCN2+]eqis used to determine the other values at equilibrium; 3% error in concentrations translates into roughly 9% error inKeq(again, this is just from the assumption and does not consider other experimental variables).
5
Checking the assumption is only part of a thorough experimental analysis; it should not be considered the main point of the lab.
Results
Complete your lab summary or write a report (as instructed).Abstract
Results
- Observations for Part 1
- λmax and absorbance at λmax for Part 2
- Beer's Law plot for Part 3 including slope(εb)
-
Ice tables, individual and average Keqvalues
Sample Calculations
- Absorbance from transmittance
- Concentration calculations
-
Keqcalculation
- Assumption testing
Discussion/Conclusions
- What you found out and how
- Relating results to predictions/theory
- How was Part 3 dependent on Part 2?
- Validity of the assumption
- What can you conclude from this experiment
