Lab 1 - Density Determinations and Various Methods to Measure Volume

Goal and Overview

This lab provides an introduction to the concept and applications of density measurements. The densities of brass and aluminum will be calculated from mass and volume measurements. To illustrate the effects of precision on data, volumes will be determined by three different methods: geometrically (measuring lengths); water displacement; and pycnometry. The composition of a mixed brass-aluminum cylinder and the volume of empty space within a hollow cylinder will also be found.

Objectives of the Data Analysis

•
Determine volume by three different methods
•
Use measured volumes and masses to calculate densities
•
Use the relationship between mass, volume, and density to find desired unknown quantities
•
Evaluate results using error analysis

Introduction

The density, ρ, of an object is defined as the ratio of its mass to its volume. Density can be useful in identifying substances. It is also a convenient property because it provides a link (or conversion factor) between the mass and the volume of a substance.

( 1 )

ρ = ^m/_V

Mass and volume are extensive (or extrinsic) properties of matter - they depend on amount. Density, an intensive (or intrinsic) property, is a kind of "heaviness" factor. In macroscopic terms, density reflects how much mass is packed into a given three-dimensional space. Typically, densities are reported g/ml or g/cm³ (which are equivalent because 1ml ≡ 1cm³). Experimentally, mass and volume measurements are required to calculate density. Masses are measured on electronic balances. Pan balances, which are accurate to ±0.01 g, are used for quick measurements where greater precision is not required. Analytical balances (accurate to ±0.0001 g) are used for more precise measurements. Volume is an amount of space, in three dimensions, that a sample of matter occupies. The number and the phase of the molecules in the sample primarily determine the volume of a substance. Volume will be measured in many ways in this course, but the units are usually milliliters (mL) or cubic centimeters (cm³). Methods for determining or delivering precise volumes include volumetric pipets and pycnometers; less precise methods include burets, graduated cylinders, and graduated pipets. In this experiment, you will measure masses and volumes to determine density. Four different metal cylinders are investigated. In parts 1-3, three different methods are used to find volume of two solid metal cylinders (Al and brass). Each method has its own degree of precision.

(i)

volume by geometry

(ii)

volume by water displacement

(iii)

volume by pycnometry (mass-based)

In parts 4-5, one method for volume determination is used to find:

(i)

the volume of a void inside a hollow cylinder; and,

(ii)

the percent composition of a mixed-metal cylinder.

Volume by geometry

A cylinder is a standard geometric form. In this case, you can measure the dimensions of the cylinder and apply the formula to calculate its volume.

( 2a )

V = π

	2

l =

d ² l where d = diameter and l = length.

Figure 1

Density would be calculated in one step to minimize rounding errors:

( 2b )

ρ =

πd ² l

The uncertainty in the volume must be determined by error propagation. Mass, length, and diameter measurements contribute to the overall uncertainty.

( 2c )

σ _ρ = ± ρ

σ _d

σ _l

σ _m

Volume by water displacement

For less defined shapes, volume can be determined by water displacement. Volumes of liquids such as water can be readily measured in a graduated cylinder. To use the water displacement method, an object (in this case, a small metal cylinder) is inserted into a graduated cylinder partially filled with water. The object's volume occupies space, displacing liquid and raising the water level. The difference between the two volumes, before and after the object was inserted, is the object's volume.

Figure 2

( 3a )

V_cyl = V_final − V_initial = V_{water + cyl} − V_water

The uncertainty of the volume is based on the two volume readings.

( 3b )

σ _{V_cyl} = σ _{V_final} + σ _{V_initial}

The density is calculated using m/V. There is not a straightforward way to find density in one step (as with geometry). The uncertainty in the density would be given by:

( 3c )

σ _ρ = ± ρ

σ _V

σ _m

Volume by pycnometry

Pycnometry is a technique that uses the density relationship between volume and mass, and the vessel used is called a pycnometer . To perform pycnometry measurements, the mass of the cylinder and the mass of a flask filled with water to a mark (A, Fig. 3) are recorded. The cylinder is then inserted into the flask. Water is displaced when the cylinder is inserted. The volume of water displaced is removed by pipet, thereby restoring the water level to the mark (B). The combined mass of the flask, remaining water, and cylinder is then measured.

Figure 3

The sums of the masses before and after are equal. The mass_A, the mass_B, and the mass_cylinder were all measured on the balance. There is only one unknown in the equation - the mass of the displaced water.

( 4a )

mass_A + mass_cylinder = mass_B + mass_{displaced water}

mass_{displaced water} = mass_A + mass_cylinder − mass_B

The volume of water removed is equal to the volume of the cylinder. Mass_water can be converted to volume using the density of water.

( 4b )

V_{displacedwater} = V_cylinder = ^{mass_{displaced water}} / _{density_water}

The density of the cylinder is calculated using m_cyl/V_cyl. The uncertainty calculation requires a few steps and assumptions. The volume of the cylinder was equal to the volume of the water. V_water was based on the three mass measurements - the mass of the cylinder, of A, and of B. The uncertainty in mass_cylinder comes from the balance reading. The uncertainty associated with mass_A and mass_B depends on your ability to precisely adjust the level of the water to the mark at the exactly same place every time (calibration). By repeatedly filling the flask to the mark and taking the mass readings, the average mass of A and the standard deviation (the fluctuation in the mass due to variations in the exact liquid level) can be found.

( 4c )

m_A

m_A,trial1 + m_{A, trial2} + m_{A, trial3} +

# trials

( 4d )

σ_{m_A} = ±

m_A

-m_A,trial1

²+

m_A

-m_A,trial2

²+

# trials-1

Assume the uncertainty in the mass of both A and B is the same: m_A ± σ_mA; m_B ± σ_mA. The uncertainty in the mass of water displaced is determined by error propagation:

( 4e )

σ_{m_water} = σ_{m_A} + σ_{m_B} + σ_{m_cyl} = σ_{m_A} + σ_{m_A} + σ_{m_cyl}

The density of water at room temperature is known quite precisely and is assumed to contribute negligible error (see table at the end of the lab), so dividing σ_{m, water} by the density of water to give σ_{V, water} is adequate. Since σ_{V, water} = σ_{V, cyl}, the uncertainty in the density can be determined.

( 4f )

σ_ρ = ± ρ

σ_V

σ_m

You will use pycnometry in parts 4 and 5 to determine the volume and/or density of a hollow cylinder and of a mixed cylinder.

Volume of a void inside a hollow cylinder

A hollow cylinder has an empty space inside.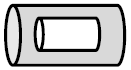

Figure 4

The volume of the cylinder is comprised of the volume of metal and the volume of the void inside.

( 5a )

V_cyl = V_metal + V_void → V_void = V_cyl - V_metal

V_cyl is determined by pyncometry. The volume occupied by the metal can be determined using the mass of the cylinder (which is due to only the metal, not the void) and the density of the metal, which was determined previously in the lab (either Al or brass, depending on the cylinder). Use the value for density that is closest to the literature values - 2.70 g/cm³ for Al; between 8 and 9 g/cm3 for brass.

( 5b )

V_metal =

m_cyl

ρ_metal

No error propagation is required

Percent composition of a mixed cylinder

The total mass of the cylinder, m_cyl, is the sum of the mass of Al and brass (m_Al + m_brass). In terms of fractional composition, this would be Xm_cyl and (1 - X)m_cyl, respectively, where X is the Al fraction and (1-X) is the brass fraction (the remainder). The cylinder volume is determined by pycnometry and is the sum of the volumes of the two metals:

( 6a )

V_cyl = V_Al + V_brass

Replace each volume by its mass divided by its density using V=m/ρ:

( 6b )

V_cyl =

m_Al

ρ_Al

m_brass

ρ_mass

Replace the masses by the equivalent expressions in terms of X and m_cyl:

( 6c )

V_cyl =

X m_cyl

ρ_Al

(1−X)m_cyl

ρ_brass

Divide through by m_cyl and replace V_cyl/m_cyl with 1/ρ_cyl:

( 6d )

ρ_cyl

ρ_Al

(1 − X)

ρ_brass

Collect terms on the right-hand side that contain X:

( 6e )

ρ_cyl

= X

ρ_Al

−

ρ_brass

Solve for X, the mass fraction of aluminum in the mixed cylinder.

( 6f )

X =

ρ_cyl

−

ρ_brass

ρ_Al

−

ρ_brass

This is the equation to use. Density of the cylinder is found by pycnometry. The densities of Al and brass have already been determined. When finding X:

Calculate each fraction in the equation, then the differences, and then the final ratio.

Use the densities of brass and aluminum determined experimentally.

Find X, and use X to determine the mass fraction of brass in the mixed cylinder, 1 - X. X has a range of possible values from zero to one (0 - 100%). If your mixed cylinder's density is between that of aluminum and of brass, you should calculate a percent of aluminum that makes sense. For example, if the mixed cylinder has a density near that of Al, X should be near one.

Equipment List

cylinders: brass, aluminum, mixed brass/aluminum, and hollow
Vernier caliper
50 mL Erlenmeyer flask, 100 mL graduated cylinder, 400 mL beaker
lab marker
Pasteur pipet
thermometer

Procedure

NOTE: IF YOU WORK WITH ANOTHER SET OF PARTNERS, MAKE SURE YOU RECORD ALL DATA. YOU WILL NOT BE ABLE TO COMPLETE THE DATA ANALYSIS IF YOUR DATA TABLES ARE INCOMPLETE. ALSO CHECK THAT DATA MAKES SENSE. Parts 1-3. Density of aluminum and brass cylinders using three different methods of volume measurement

Part 0: Measure metal cylinder masses.

Obtain four cylinders - brass, aluminum (solid cylinders marked S), hollow (marked H), mixed brass/aluminum (marked P for "plugged"). Return cylinders to the stockroom at the end of lab.

Record the cylinders' numbers.

Record the masses of the cylinders on the analytical balance to the 0.0001 g (the uncertainities in your cylinders' masses are ±0.0001 g). You will use these masses throughout the experiment.

Part 1: Volume by Geometry

Measure the diameter and length of each cylinder using the Vernier calipers. Your TA will help you if you need it. Record the values to the 0.01 cm (each measurement is ±0.01 cm).

Determine the density of the cylinder. Find the uncertainity using error propagation.

Part 2: Volume by Displacement

Put enough water to cover the metal cylinder into a 100-mL graduated cylinder and record the volume. The graduated cylinder is not very precise; readings will be ±0.5 mL (the digit in the tenths place will either be a 5 or a 0).

Carefully slide the metal cylinder down the side of the graduated cylinder into the water. Tossing it in can break the bottom of the graduated cylinder.

With the metal cylinder completely submerged, record the new volume reading (to ±0.5 mL).

Determine the volume of the metal cylinder. Calculate the uncertainty in your volume using error propagation.

Determine the density of the cylinder. Calculate the uncertainty using error propagation.

Part 3: Volume by Pycnometry

Fill a 400 mL beaker with water and measure its temperature. Use this water throughout the experiment. Assume that the density of water makes a negligible contribution to the overall uncertainty in the values calculated.

Make your pycnometer.

a
Draw a ring midway up the neck of a 50 mL Erlenmeyer flask with a waterproof marker or wax crayon, as shown below.
b
Invert the flask on the table; hold marker on top of something solid; and, rotate the flask while marking the neck at a constant height.

Figure 5

Calibrate your pycnometer. How well can you adjust the water's meniscus to the top of the line drawn? Precise filling to that mark increases reproducibility (and data quality). Practice with the pycnometer before making measurements. Your TA will demonstrate. The pycnometer filled with water to the mark is called 'A'.

a
Use a disposable pipet to add and remove drops of water to adjust the meniscus to the top of the line.
b
Record the mass of the flask and water. No drops should appear on the neck of the flask above the water line.
c
Pour out the water into your 400-mL beaker; refill to the mark; reweigh.
d
Repeat step c until you have three similar values for the mass of 'A'.
e
Determine the average m_A and its standard deviation (σ_mA). The standard deviation, σ_mA, reflects your ability to reproducibly fill the pycnometer to the same place every time you use it; σ_mA is the uncertainity of the pycnometer and should be read with the average mass of 'A' as well as the mass of 'B' (parts 3, 4, and 5).
f
If you share data with another set of students, make sure to record their calibration data as well. You must use the correct calibration result with the appropriate data. In your lab notebook, label which cylinders go with which pycnometer calibration.

Indirectly measure the mass of water displaced by your solid cylinders. The pycnometer containing the metal cylinder with water filled to the mark is called 'B'.

a
Carefully insert a metal cylinder, fill with water to the mark, and record the mass (the flask with water and cylinder).
b
Repeat filling and weighing several times until the data appears reproducible.
c
Calculate the mass of the water removed. Convert this mass to volume by dividing by the density of water (use a precise value, specific to the water's temperature). This volume equals the volume of the metal cylinder.
Calculate the uncertainty in the mass of water removed using error propagation. Convert this mass to volume units by dividing by the density of water (use a precise value, specific to the water's temperature). This value equals the uncertainity in the volume of the metal cylinder.
e
Repeat with the other cylinders as instructed.

Determine the density of each cylinder. Include the uncertainties.

Please do not throw the metal cylinders away. Please return them to the reagent bench. Please put disposable pipets (and any broken glassware) in broken glass containers, not the trash can. You will lose points for inappropriate disposal.

Part 4: Determine Void Volume in a Hollow Cylinder by Pycnometry

For the hollow cylinder, record identity of metal of the hollow cylinder (either aluminum or brass). You recorded its mass at the beginning of the experiment.

Insert the cylinder into the pycnometer; remove the water above the line, and record the new mass.

Determine the volume of the cylinder and calculate the volume of the void. No error propagation.

Part 5: Mass Fraction of Al and Brass Determination for Mixed-metal Cylinder by Pycnometry

You recorded its mass of the mixed metal cylinder at the beginning of the experiment.

Insert the mixed Al/brass cylinder into the pycnometer, remove the water above the line, and record the mass.

Determine the density of the cylinder and the mass fractions of Al and of brass (X and 1-X, respectively). No error propagation.

Reporting Results

Complete your lab summary or write a report (as instructed).

Results / Sample Calculations

Masses and volumes for solid cylinders by each method
%error relative to literature values (ρ_Al = 2.70 g/cm³; ρ_Al = 8.44 g/cm³, depending on the alloy's composition)
Void volume
Mass fraction
Error analysis for parts 1-3

Discussion

What you found out (refer to results tables) and how for all 5 parts
What were the major experimental sources of error?
Compare the three methods used to determine volume - which method was more accurate and why? Which was most precise?
What could be done to improve the precision in any or all of the methods?
How does the instrument error compare to standard deviation error?

Review Questions

Whole degrees are listed down the left hand side of the table, while tenths of a degree are listed across the top. So to find the density of water at 5.4 °C, find the whole degree by searching down the left hand column to '5'. Then slide across that row to '0.4'. The density of water at 5.4 °C is 0.999957 g/mL.

Lab 1 - Density Determinations and Various Methods to Measure Volume

Goal and Overview

Objectives of the Data Analysis

Suggested Review and External Reading

Introduction

Volume by geometry

Volume by water displacement

Volume by pycnometry

Volume of a void inside a hollow cylinder

Percent composition of a mixed cylinder

Equipment List

Procedure

Part 0: Measure metal cylinder masses.

Part 1: Volume by Geometry

Part 2: Volume by Displacement

Part 3: Volume by Pycnometry

Part 4: Determine Void Volume in a Hollow Cylinder by Pycnometry

Part 5: Mass Fraction of Al and Brass Determination for Mixed-metal Cylinder by Pycnometry

Reporting Results

Results / Sample Calculations

Discussion

Review Questions