Ohm's Law and Electrical Circuits

Introduction

In this experiment, you will measure the current-voltage characteristics of a resistor and check to see if the resistor satisfies Ohm's law. In the process you will learn how to use the multimeter to measure voltage, current, and resistance. You will then test some of the laws of circuit theory. When a potential difference, V, is applied across a conductor, an electrical current, I, will flow from the high potential end to the low potential end. In general the current will increase with the applied voltage (potential difference). A plot of the current as a function of the voltage is called the current-voltage (I-V) characteristic. If the I-V characteristic is a straight line, as in Fig. 1, then we say that the piece of conductor satisfies Ohm's law: V = IR, where R is a constant defined to be the resistance and has units of volts/ampere, or Ω (ohm).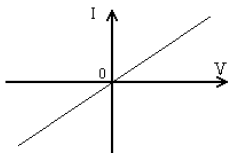

Figure 1: I-V curve for an ohmic material

In an electrical circuit, the wires that are used to connect the circuit elements do have resistance. However, the resistances of the wires are usually negligible compared with the resistances of the circuit elements. There are specific elements called resistors that control the distribution of currents in the circuit by introducing known resistances into the circuit. The currents and voltages at different parts of the circuit can be calculated by using circuit theory that will be discussed later. There are many kinds of resistors but the most common ones are the carbon composite resistors shown below. These resistors are small brown cylinders with colored bands. The color bands follow a color code giving the resistance to within a specified manufacturing tolerance.

Figure 2

In this lab you will be studying only simple DC circuits consisting of a power source and one or more resistors connected with wires whose resistances are negligible compared to those of the resistors. The basic theory for analyzing the circuit is summarized by two laws known as Kirchhoff's Rules:

1
Kirchhoff's Loop Rule
The total change in the voltage around any closed loop is zero. This is obvious when you consider that voltage is a difference of potential. This rule just says that the difference of potential from one point to that same point is zero, no matter how you go around the circuit.
2
Kirchhoff's Junction Rule
The amount of current flowing into any point on a wire (or into a junction of wires) is always equal to the amount of current flowing out of it.

Two types of resistor connections are usually found in a circuit, the series and the parallel connection shown in Fig. 3.

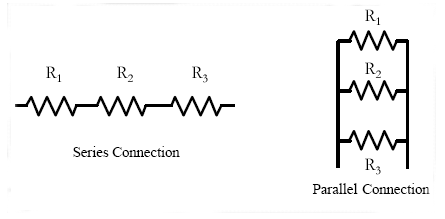
Figure 3

Using Kirchhoff's Rules it can be shown that the three resistors in series are equivalent to a single resistor with equivalent resistance, R, given by:

( 1 )

R = R₁ + R₂ + R₃ (resistors in series)

Likewise, the three resistors connected in parallel are equivalent to a single resistor with equivalent resistance, R, given by:

( 2 )

R₁

R₂

R₃

(resistors in parallel)

Apparatus

The apparatus for this experiment consists of a regulated power supply and two multi-meters. These pieces of equipment are described below.

Regulated Power Supply

Figure 4

The regulated power supply and its symbol in a circuit are shown above. This power supply converts the output from a regular 110 V, 60 Hz AC outlet into a constant DC power source with variable voltage from 0 to 20 V. It produces a maximum current of 0.5 A. Turning the control knob on the device can vary the output voltage. It is good practice to always start from the zero voltage and gradually increase it to the desired value. The output is obtained through the red and black jacks. By convention, the red jack is the positive terminal and the black jack is the negative terminal.

Measuring Currents, Voltages, and Resistances

When the multi-meter is set to measure current it serves as an ammeter, when it is set to measure voltages, it serves as a voltmeter, and when it is set to measure resistances, it serves as an ohmmeter. The symbols for the ammeter, voltmeter and the ohmmeter are given below.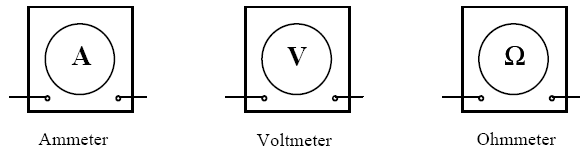

Figure 5

To measure the current flowing through an object such as a resistor, the ammeter is connected in series with the object as shown in Fig. 6a. Ammeters have very low resistance so that when they are placed in a circuit, they do not significantly affect the total circuit resistance and hence the current to be measured. To measure the voltage across an object such as a resistor, the voltmeter is connected in parallel with the object as shown in Fig. 6b. Voltmeters have very large resistance so that only a small portion of the circuit's current will be diverted through the voltmeter. To measure the resistance of an object such as a resistor, the ohmmeter is connected to the object as shown in Fig. 6c. If the resistor is connected to a circuit, then one end of the resistor must be disconnected from the circuit while making this measurement. The battery in the multi-meter supplies the current necessary for measuring the resistance so that no external power supply is needed.

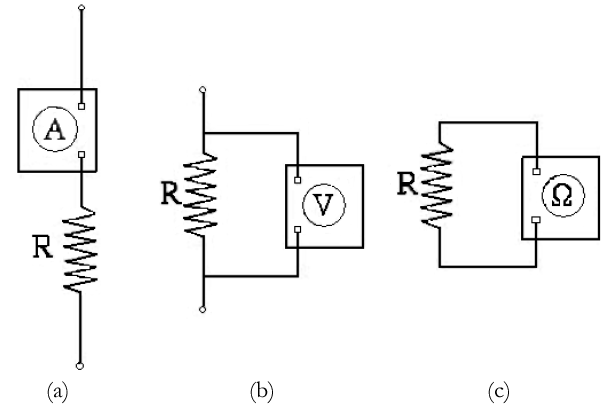
Figure 6

Making Simultaneous Current and Voltage Measurements

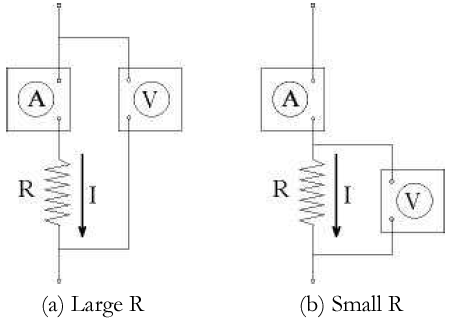
Figure 7

There are two ways of making simultaneous measurements of A and V as shown in Fig. 7a and Fig. 7b. In Fig. 7a, the ammeter measures the current in the resistor R, but the voltmeter does not measure the voltage across the resistor, V_R. Instead it measures the voltage across the resistor plus the voltage on the ammeter, V_A. Since V_R + V_A = IR + IR_A, where R_A is the resistance of the ammeter, the voltmeter measurement will be approximately equal to V_R if R is much larger than the resistance of the ammeter. Ammeters typically have resistances of 0.001 Ω or less. Using method (a) to measure the voltage on a resistor with a small resistance, say 0.1 Ω, would produce an error in the voltage of IR_A / IR = 0.001/0.1 or a 1% error. On the other hand, for a large resistance, say R = 1000 Ω, the error reduces to

IR_A / IR = 0.001/1000 or 0.0001%.

The method illustrated in Fig. 7a should therefore be used to measure large resistances. In Fig. 7b, the voltmeter measures the voltage across the resistor R, but the ammeter does not measure the current through the resistor, I. Instead it measures the current through the resistor plus the current through the voltmeter, I_V. The sum of these currents is given by:

( 3 )

I + I_V =

V_R

R_V

where R_V is the resistance of the voltmeter. Therefore, the ammeter measurement will be approximately equal to I if R is much smaller than R_V. Voltmeters typically have resistances of 100,000 Ω or more. Using method (b) to measure the current on a resistor with large resistance, say 1000 Ω, will produce an error in the measured current of I_V / I = R / R_V = 1,000/100,000 or a 1% error. For a small resistance, say R = 0.1 Ω, the error reduces to

R / R_V = 0.1/100,000 or 0.0001%.

The method illustrated in Fig. 7b should be therefore be used to measure small resistances.

Procedure

Resistance Measurements

1
Using the multimeter as an ohmmeter, measure and record the resistances of each of the three resistors provided. Remember to include uncertainty estimates based on the accuracy of the meter.
2
Connect the three resistors in series. Record the equivalent resistance determined with the ohmmeter.
3
Connect the three resistors in parallel. Record the equivalent resistance determined with the ohmmeter.

Current-Voltage Characteristics of a Resistor

This part of the experiment requires you to simultaneously measure the current and voltage on a resistor. The resistors used in this experiment have resistances of about 1000 Ω. Therefore, the method shown in Fig. 7a should be used to simultaneously measure I and V.

1
Select the resistor with about a 600 Ω resistance. Connect the power supply (do not turn it on yet), the voltmeter, the ammeter, and the resistor according to the circuit diagram shown in Fig. 7a. You may use the Fluke 77 as an ammeter and the Micronta as a voltmeter. Since the voltage of the power supply is about 10 V, the current will be of the order of milliamperes. Thus the "300 mA" and the "COM" terminals on the Fluke 77 should be used for the ammeter connection.
2
Have your lab instructor check your circuit before you turn on the power supply.
3
With the control knob at the minimum setting (fully counterclockwise), turn your power supply on. Turn the control knob up until the voltmeter reads about one volt. Record the current and the voltage.
4
Increase the voltage in steps of 2 V. Measure and record the current and the voltage. Stop when the voltage reaches about 15 Volts.
5
Turn the control knob on the power supply fully counterclockwise and turn the power switch off.
6
Check your data by making a rough plot of V vs. I on the data sheet or a piece of graph paper. Check if your plot agrees with Ohm's Law. Check if the slope of your plot gives the correct resistance.
7
Repeat the above steps to measure the V vs. I characteristics of a light bulb (#53, 120 mA at 14 V). Use the same circuit but replace the resistor with the light bulb. Take data readings in current steps of 10 mA up to a maximum of 100 mA.

Kirchhoff's Rules

In this experiment you will verify Kirchhoff's rules on a simple circuit shown below.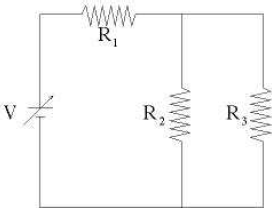

Figure 8

1
Connect the three resistors and the power supply according to the circuit diagram above. Be sure to identify and record the values of the three resistors.
2
Have your lab instructor check your circuit before you turn on the power supply.
3
Turn on the power supply and adjust the control knob until the power supply voltage is about 10 V. Record the output voltage V and keep it fixed for the remaining experiment.
4
Measure and record the voltages V₁, V₂, and V₃ across each of the resistors. Remember to include uncertainty estimates for each of your measurements based on the accuracy rating of the meter.
5
Measure and record the currents I₁, I₂, and I₃ through each of the resistors, along with appropriate uncertainty values. Because the power supply is always on for this measurement, it is easy to blow the fuse on your multimeter if it is not connected properly. Turn off the multimeter when you are making the connection. Make sure that the multimeter is in series with the resistor you are measuring before turning it on. If you are not sure, check with your instructor.
6
Turn off the multi-meter and the power supply when you are finished with the experiment.

When you are finished with the experiment, please clean up your work area and return all the wires and clips to their storage bins. Be sure that you and your instructor initial your data sheet(s), and that you hand in a copy of your data before you leave the lab.

Data Analysis

Resistance Measurements

For this part we shall denote the calculated equivalent resistance by R_T, and the measured equivalent resistance by R.

1
Calculate the sum R_T of the resistances for the three resistors R₁, R₂, and R₃ connected in series.
2
What are the uncertainties
u_R₁, u_R₂, u_R₃
in your measurements of the resistances? What is the source of the uncertainty?
3
Using your values for the uncertainties of the three resistors, calculate the uncertainty of the sum u_{R_T} by using the propagation of uncertainty formula for the sum.
4
Summarize your values of R and R_T, including uncertainties.
5
Calculate the total resistance
R_T
for the parallel connection.
6
Using the propagation of uncertainty formula for a ratio, show that the fractional uncertainty of f is the same as the fractional uncertainty of 1/f, i.e. show
u_f
f
=
u_1/f
1/f
.
7
Using the equation in step 6, calculate the uncertainties of 1/R₁, 1/R₂ and 1/R₃. Then, using the propagation of uncertainty for the sum, calculate the uncertainty of 1/R_T from the uncertainties of 1/R₁, 1/R₂ and 1/R₃. Finally, again using the equation in step 6, calculate the uncertainty of R_T from the uncertainty of 1/R_T.
8
Summarize your values of R and R_T, including uncertainties.

Current Voltage Characteristics of a Resistor and a Light Bulb

1
Prepare two tables (one for the resistor and one for the light bulb) of currents and the voltages from the data obtained.
2
Make a scatter-plot of V vs. I for the resistor data.
3
Generate a least-square linear fit of your plot to Ohm's law: V = IR. What do the slope and intercept parameters in the fit correspond to?
4
Summarize the value of R (measured by a multimeter) and the fitted value of R, including uncertainties.
5
Make a scatter-plot of V vs. I for the light bulb data.

Kirchhoff's Loop and Junction Rules

1
What are the uncertainties in your measurements of the currents I₁, I₂, and I₃? Based on these uncertainties, check if the currents you measured satisfy the junction rule, i.e. I₁ = I₂ + I₃.
2
There are three loops in the circuit used in this part. Write down the equation given by the loop rule for each loop. Based on the uncertainties in your measurements of V₁, V₂, and V₃, verify that the voltages you measured satisfy the equations derived from the loop rule.

Discussion

Summarize the results for the section on Resistance Measurements. Which of the connection, series or parallel, gave the least total resistance? Why? Does your measured value of the total resistance of the series connection and the parallel connection agree with the calculated equivalent resistance? Describe the current-voltage characteristics of the resistor studied in the section on Current-Voltage Characteristics of a Resistor. Is the current zero when the voltage is zero? If not, explain the discrepancy. Did the result agree with Ohm's law? What is the value of the resistance obtained from the least square fit and how does it compare with the value measured with the ohmmeter? Compare the V-I plots for the resistor and light bulb. From the "shape" of V-I plot for the light bulb, what can you conclude about the resistance of the light bulb? In the section on Kirchhoff's Rules, did your current measurements satisfy the junction rule? Did your voltage measurement satisfy the loop rule? Do your comparison quantitatively, taking uncertainties in the measurements into account. In addition to the uncertainty of the measuring instrument, does the connection of the ammeter or voltmeter to the circuit cause additional uncertainty? If so, are these uncertainties significant?