Lab 6 - Mixtures of Acids and Bases
Purpose
To investigate the resulting pH's of different mixtures of acid and base solutions.Goals
-
•To calculate the pH of pure acid and base solutions.
-
•To calculate the pH of mixtures of acid and base solutions.
-
•To measure the pH of pure acid and base solutions and mixtures of these solutions.
-
•To compare the resulting pH's of different mixtures of acid and base solutions.
Introduction
Brønsted acids are defined as proton donors. When placed in water, Brønsted acids (HA) donate a proton to water to produce the conjugate base of the acid(A−)
and a hydronium ion (H3O+) according to the following reaction.
( 1 )
HA + H2O 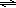 A– + H3O+
A– + H3O+
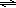 A– + H3O+
A– + H3O+Strong Acids:
The Ka's for strong acids, such as HCl and HNO3, are simply listed as >> 1 which indicates that they dissociate 100% when placed in water.( 2 )
HCl + H2O → Cl− + H3O+
pH = −log[H3O+].
Weak Acids:
Weak acids, such as NH4+ and HC2H3O2, only partially dissociate in water according to their Ka's. As with any equilibrium reaction, the equilibrium concentrations can be calculated by generating a reaction table and substituting into the Ka expression. For example, acetic acid, HC2H3O2, has a Ka of1.8 × 10−5.
So for a 0.2 M aqueous solution of HC2H3O2, the equilibrium concentrations can be calculated as follows.
| HC2H3O2 | + | H2O | 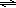 | C2H3O2− | + | H3O+ | |
| initial | 0.2 M | 0.0 M | 0.0 M | ||||
| Δ | −x | +x | +x | ||||
| equilibrium | 0.2 − x M | x M | x M | ||||
( 3 )
Ka =
| ||||||
| x = 1.9 × 10−3 M |
[HC2H3O2] = 0.2 M
and [C2H3O2−] = [H3O+] = 1.9 × 10−3 M.
Equation 3 Ka =
| ||||||
| x = 1.9 × 10−3 M |
Ka =
| ||||||
| x = 1.9 × 10−3 M |
( 4 )
[H3O+] = (Ka × cwa)1/2 = (1.8 × 10−5 × 0.2)1/2 = 1.9 × 10−3 M
−log[H3O+]
to get 2.72.
Similarly, Brønsted bases (B−)
are defined as proton acceptors and when placed in water will accept a proton from water to produce the base's conjugate acid (HB) and a hydroxide ion (OH−).
( 5 )
B− + H2O 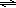 HB + OH−
HB + OH−
 HB + OH−
HB + OH−( 6 )
Ka × Kb = Kw = 1.0 × 10−14
Strong Bases:
The most common strong bases found in the laboratory are the Group IA salts of hydroxide, which completely dissociate in water to give one equivalent ofOH−.
( 7 )
NaOH(s) → Na+(aq) + OH−(aq)
[OH−] = [strong base concentration]
and the pOH = −log[OH−].
At 298 K, the relationship between pH and pOH is:
( 8 )
pH = 14 − pOH.
Weak Bases:
Sodium acetate, NaC2H3O2, is considered a weak base. Using equation 6Ka × Kb = Kw = 1.0 × 10−14
above, the Kb for C2H3O2−
is (1.0 × 10−14) / (1.8 × 10−5) = 5.6 × 10−10.
Using this value and a reaction table, the equilibrium composition of a 0.2 M NaC2H3O2
solution can be calculated as follows.
| C2H3O2− | + | H2O |  | HC2H3O2 | + | OH− | |
| initial | 0.2 M | 0.0 M | 0.0 M | ||||
| Δ | −x | +x | +x | ||||
| equilibrium | 0.2 − x M | x M | x M | ||||
( 9 )
Kb =
| ||||||
| x = 1.1 × 10−5 M |
[C2H3O2−] = 0.2 M
and [HC2H3O2] = [OH−] = 1.1 × 10−5 M.
Equation 9 Kb =
| ||||||
| x = 1.1 × 10−5 M |
[OH−]
for a weak base. In cases where the percent ionization of the base is less than 5%, equation 9 Kb =
| ||||||
| x = 1.1 × 10−5 M |
( 10 )
[OH−] = (Kb × cwb)1/2 = (5.6 × 10−10 × 0.2)1/2 = 1.1 × 10−5 M
−log[OH−]
to get 4.98. Using equation 8pH = 14 − pOH.
, the pH of the 0.2 M C2H3O2−
solution is 14 − 4.98 = 9.02.
When acids and bases are mixed together, things become more complicated. No matter how complicated, all mixtures of acids and bases should be approached the same way.
-
1Determine what species actually exist in solution. Any sodium or potassium salt will dissociate completely as will any strong acid or base.
-
2Write out a balanced chemical reaction to describe any interactions that will occur. Remember that the reactants must be present in the original solution as identified in step 1. Look for possible Ka or Kb reactions. Or for reactions of a weak base with a hydronium ion or a weak acid with a hydroxide ion that will react 100%. Sometimes there will not be an appropriate chemical reaction!
-
3Generate a reaction table based on the balanced chemical reaction. Remember that the initial concentrations for the products are not necessarily zero!
-
4Calculate the equilibrium composition of the mixture. This is only possible if the equilibrium constant for the reaction is known or if the reaction goes to completion.
-
5Calculate the pH. Once the[H3O+]or[OH−]is known, the pH can be calculated as above in the pure solutions.
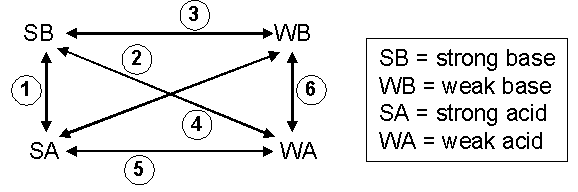
Figure 1: Combinations of Acids and Bases
Mixture 1:
Mixture 1, reaction of a strong acid and strong base, goes to completion. A reaction table can be used to determine if excess acid or base remains. For example, consider the addition of 10. mL of 0.10 M HCl to 15 mL of 0.20 M NaOH. Since two solutions are being mixed, it is better to use moles or mmoles in your reaction table.| H3O+ | + | OH− | → | H2O | + | H2O | |
| given | 10. mL × 0.10 M | 15 mL × 0.20 M | |||||
| initial | 1.0 mmol | 3.0 mmol | - | - | |||
| Δ | −1.0 mmol | −1.0 mmol | - | - | |||
| final | 0 mmol | 2.0 mmol | - | - | |||
[OH−]
can be calculated from the final mmol/(total volume) to give 2.0 mmol/(10 + 15 mL) = 0.08 M. Table 1 contains the necessary formulas to calculate pOH and pH from this information. The pH of this mixture is 12.90.

Mixture 2:
Mixture 2, reaction of a strong base and weak acid, also goes to completion. Depending upon the relative amounts of material, the final solution may be composed of only strong base, only weak base, or a mixture of weak acid and weak base. For example, consider the addition of 15. mL of 0.20 M NaOH to 10. mL of 0.30 M HC2H3O2. Since two solutions are being mixed, it is better to use moles or mmoles in your reaction table.| HC2H3O2 | + | OH− | → | C2H3O2− | + | H2O | |
| given | 10. mL × 0.30 M | 15 mL × 0.20 M | |||||
| initial | 3.0 mmol | 3.0 mmol | - | - | |||
| Δ | −3.0 mmol | −3.0 mmol | +3.0 mmol | - | |||
| final | 0 mmol | 0 mmol | 3.0 mmol | - | |||
[C2H3O2−]
can be calculated from the final mmol/(total volume) to give 3.0 mmol/(10 + 15 mL) = 0.120 M. Table 1 contains the necessary formulas to calculate the pH, given the concentration of weak base. The pH of this mixture is 8.91.
Mixture 3:
Mixture 3, a strong base and weak base, does not have any reaction. Rather, the[OH−]
associated with the strong base tends to suppress generation of [OH−]
from the reaction of the weak base and water. Please consult your textbook for more details. In compositions such as this, the pH can be readily obtained by focusing upon the concentration of strong base. For example, consider the addition of 20. mL of 0.20 M NaOH to 10. mL of 0.20 M NaC2H3O2. This results in dilution of the strong base. In this example, [OH−]
= mmol NaOH/total volume = 20 mL × 0.20 M OH− / (20. + 10. mL) = 0.13 M.
Table 1 contains the necessary formulas to calculate pOH and pH from this information. The pH of this mixture is 13.12.
Mixture 4:
Mixture 4, reaction of a strong acid and weak base, also goes to completion. Depending upon the relative amounts of material, the final solution may be composed of only strong acid, only weak acid, or a mixture of weak acid and weak base. For example, consider the addition of 15. mL of 0.20 M HCl to 20. mL of 0.20 M NaC2H3O2. Since two solutions are being mixed, it is better to use moles or mmoles in your reaction table.| H3O+ | + | C2H3O2− | → | HC2H3O2 | + | H2O | |
| given | 15. mL × 0.20 M | 20 mL × 0.20 M | |||||
| initial | 3.0 mmol | 4.0 mmol | - | - | |||
| Δ | −3.0 mmol | −3.0 mmol | +3.0 mmol | - | |||
| final | 0 mmol | 1.0 mmol | 3.0 mmol | - | |||
( 11 )
pH = pKa + log
or pH = pKa + log
.
 |
| [base] |
| [acid] |
 |
 |
| moles of base |
| moles of acid |
 |
pH = −log(1.8 × 10–5) + log(1.0 mmol C2H3O2− / 3.0 mmol HC2H3O2) = 4.26.
Mixture 5:
Mixture 5, a strong acid and weak acid, also does not have any reaction. The [H3O+] associated with the strong acid tends to suppress generation of [H3O+] from the reaction of the weak acid and water. In compositions such as this, the pH can be readily obtained by focusing upon the concentration of strong acid. For example, consider the addition of 30. mL of 0.20 M HCl to 20. mL of 0.15 M HC2H3O2. This results in dilution of the strong acid. In this example, [H3O+] = mmol HCl/total volume = 30 mL × 0.20 M H3O+ / (30. + 20. mL) = 0.12 M. The pH = –log[H3O+] = 0.92.Mixture 6:
Mixture 6, the combination of a weak acid and a weak base, is also a buffer. The pH can be calculated using the Henderson-Hasselbalch equation. For example, consider the mixture of 10. mL of 0.1 M NH4Cl and 15 mL of 0.10 M NH3. For this example,pH = −log(5.6 × 10–10) + log(1.5 mmol NH3 / 1.0 mmol NH4+) = 9.43.
This is a brief summary of calculating the pH of pure acid and base solutions as well as mixtures of acid and base solutions. In this lab, you will explore these solutions in more detail and gain a greater understanding of equilibrium in aqueous acid/base mixtures.
Equipment
-
1 25 × 150 mm test tube
-
1 400 mL beaker (to hold the test tube)
-
1 glass stir rod
-
1 10 mL graduated cylinder
-
1 100 mL beaker
-
2 30 mL beakers
-
1 MicroLab interface
-
1 MicroLab pH measurement instruction sheet
-
1 pH electrode in pH 7.00 buffer
-
1 ring stand
-
1 clamp
-
1 250 mL beaker for electrode rinsings
-
1 deionized water squirt bottle
-
1 box Kimwipes
Reagents
-
~60 mL 0.1 M NaOH
-
10 mL 0.1 M HCl
-
10 mL 0.1 M NH4Cl
-
10 mL 0.1 M NaC2H3O2
-
~15 mL pH 4.00 buffer
-
~15 mL pH 7.00 buffer
-
~15 mL pH 10.00 buffer
Safety
HCl and NaOH are corrosive. They can attack the skin and cause permanent damage to the eyes. If either solution splashes into your eyes, use the eyewash immediately. Hold your eyes open and flush with water. If contact with skin or clothing occurs, flush the affected area with water. Have your lab partner notify your instructor about the spill.Waste Disposal
All solutions can be flushed down the sink with plenty of water.Prior to Class
Please enter the calculated pH values from the WebAssign pre-lab assignment in Table A on your printed worksheet.Lab Procedure
Please print the worksheet for this lab. You will need this sheet to record your data. In this experiment, you will be using pH electrodes connected to the MicroLab interface. pH electrodes have a thin glass bulb at the tip. They break easily and are costly to replace. Be careful not to shove the electrode into the bottom of a beaker or drop the electrode. There is a protective guard around the tip, which should remain in place at all times. The guard will not protect against careless treatment. Please use extreme care when using this equipment. Best results in using the electrodes are obtained if:-
•Electrodes are kept in standard pH 7 buffer solution when not in use.
-
•Immediately prior to use, the electrodes are rinsed with deionized water and gently blotted with a tissue, then placed in the test solution.
-
•The electrodes are rinsed and blotted again after the measurement and returned to the pH 7 buffer solution.
Part A: Calibrating the MicroLabTM pH Electrode
1
Open the MicroLab program.
2
Make sure the pH electrode is plugged into the interface.
3
Calibrate the pH electrode using the MicroLab instructions provided in the lab. The calibration standards for the pH electrode will be a pH = 4.00 (red) buffer solution, a pH = 7.00 (yellow) buffer solution, and a pH = 10.00 (blue) buffer solution. Use about 15 mL of each in 30 mL beakers.
4
After the calibration is complete, configure the MicroLab program to collect data as described in the lab.
Part B: Measuring the pH of Acid/Base Mixtures
1
In a 100 mL beaker, obtain ~70 mL of 0.1 M NaOH from the side shelf.
2
Measure 10.0 mL of deionized water using the 10 mL graduated cylinder. Carefully pour the water into the 25 × 150 mm test tube and place it in the 400 mL beaker for support.
3
Measure the pH of the deionized water and record it in Table A.
-
aRemove the electrode from the buffer, rinse the electrode with deionized water and blot it with a Kimwipe.
-
bDuring measurement, place the electrode such that it is immersed in the sample solution and swirl the beaker gently, allowing a few seconds for equilibration.
-
cAfter the measurement is recorded, rinse the electrode with deionized water and blot it with a Kimwipe. Then return it to the pH 7 buffer provided.
4
Measure 5.0 mL of 0.1 M NaOH using the graduated cylinder. Carefully add the NaOH to the water in the test tube. Use the glass stir rod to gently mix the solution.
5
Measure the pH of the deionized water plus 5.0 mL of NaOH and record it in Table A.
6
Again measure 5.0 mL of 0.1 M NaOH using the graduated cylinder and carefully add it to the solution in the test tube. Use the glass stir rod to gently mix the solution.
7
Measure the pH of the deionized water plus 10.0 mL of NaOH and record it in Table A.
8
One more time measure 5.0 mL of 0.1 M NaOH using the graduated cylinder and carefully add it to the solution in the test tube. Use the glass stir rod to gently mix the solution.
9
Measure the pH of the deionized water plus 15.0 mL of NaOH and record it in Table A.
10
Pour your solution down the sink and flush with tap water. Rinse out the test tube with deionized water and dry as best as you can.
11
Repeat steps 2 - 10 substituting 0.1 M HCl for the deionized water.
12
Repeat steps 2 - 10 substituting 0.1 M NH4Cl for the deionized water.
13
Repeat steps 2 - 10 substituting 0.1 M NaC2H3O2 for the deionized water.
14
After your last measurement, stop and close the MicroLab software. Rinse all of your glassware with water, dry it and return it to the set-up area where you found it. Make sure the pH electrode is submerged in the pH 7 buffer solution.
15
Before leaving, enter your results in the in-lab assignment. If all results are scored as correct, log out. If not all results are correct, try to find the error or consult with your lab instructor. When all results are correct, note them and log out of WebAssign. The in-lab assignment must be completed by the end of the lab period. If additional time is needed, please consult with your lab instructor.

