Energy of a Rolling Object
Introduction
In this experiment, we will apply the Law of Conservation of Energy to objects rolling down a ramp. As an object rolls down the incline, its gravitational potential energy is converted into both translational and rotational kinetic energy. The translational kinetic energy is( 1 )
KEtrans = (1/2)mv2
( 2 )
KErot = (1/2)Iω2
( 3 )
I = kmr2
-
k = 2/5 = 0.4 for a uniform solid sphere, k = 1/2 = 0.5 for a uniform disk or solid cylinder, k = 1 for a hoop or hollow cylinder.
v = rω.
Substituting equation 3I = kmr2
and the expression for v into equation 2KErot = (1/2)Iω2
, we obtain:
( 4 )
KErot = (1/2)kmv2
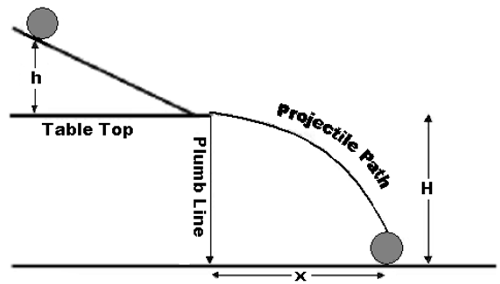
Figure 1
| total energy at top of ramp = total energy at bottom of ramp, |
| Egravitational = Etranslational + Erotational |
( 5 )
mgh = (1/2)mv2 + (1/2)kmv2.
( 6a )
x = vt
( 6b )
H = (1/2)gt2
x = vt
and 6bH = (1/2)gt2
) can be combined, eliminating t, to obtain the following expression for the velocity in terms of x and H.
( 7 )
v2 = gx2 / 2H
Procedure
Part 1
-
1Level the bottom surface of the ramp and the tray.
-
2Choose one object from the collection of solid spheres, solid cylinders, and circular rings provided. Identify the size and weight of this object by recording its diameter and mass.
-
3Roll the object down the ramp, starting from the top of the ramp, noticing at what point the object lands in the catch tray. Adjust the tray so that this point is towards the far end of the tray.
-
4A sheet of white paper taped in the tray and overlaid by a piece of carbon paper ("carbonized" face down) will record the impact point of the object. Use only one sheet of carbon paper and do not tape it down, move it around to record the impacts! From the impact point you can determine x. Choose at least 6 heights, h, from 15 cm to 35 cm and roll the object down the ramp several times from each height. State very specifically how you determine the height h. Try to catch the object after the first bounce to avoid stray marks on the paper.
-
5Measure the horizontal distance from the edge of the table to each mark, and enter this distance as x in Table 1. Plumb bobs will help you find the right point from which to measure (your instructor will demonstrate this). It's a good idea to check periodically to make sure that your tray has not shifted under the impact of the objects, which would introduce error.
-
6Take several measurements of H, the distance the object falls from the bottom of the ramp.
Part 2
Select 5 different objects and record descriptive information about the physical characteristics of each object (shape, mass, diameter, etc.). Before you roll each object down the ramp, predict and record the relative horizontal distance that each will travel (rank order). Roll each object several times from the same initial height to observe the differences in the horizontal distances each lands from the end of the ramp. Be careful to use a procedure to ensure that objects of different radii roll through the same vertical distance, h, and explain the method you used to accomplish this task. Measure and record the average x for each object.
Be sure to initial your data, have your TA initial your data, and hand in a copy before you
leave the lab room.
Analysis
Part 1
-
1Complete the data tables with the information needed to compute the initial potential energy and the translational and rotational kinetic energies for each release height. Calculate these energy values and determine the percentage of energy "lost" to non-conservative factors that were assumed to be negligible. What affect does the release height have on your results?
-
2Estimate the uncertainty in your measurements and compare with the fractional loss of energy. Based on this comparison, was mechanical energy conserved?
