Uniform Circular Motion
Introduction
Uniform circular motion is the motion of an object traveling at a constant (uniform) speed in a circular path. Besides the speed, there are several other variables that are used to characterize the motion. They are the radius of the motion r, the angular speed ω, the period T, and the rotational frequency f. The period is the time required for the object to complete one revolution of motion. The angular speed is the angular displacement per second and it is related to the frequency by:( 1 )
ω = 2πf
( 2 )
f =
| 1 |
| T |
( 3 )
a =
= rω2
| v2 |
| r |
( 4 )
F = ma = mrω2
UCM Apparatus
The UCM apparatus consists of a variable-speed rotating platform. A distance r from the center of rotation is the side post assembly from which hangs an object of mass m, referred to as the rotating mass (not to be confused with the static mass). The rotating mass is attached to a spring on the center post by way of a string and small pulley. When the platform rotates, the rotating mass will travel in a circular path due to the force exerted on it by the string (by way of the tension in the spring). Since it is not possible to have an instantaneous readout of this tension force while the platform is rotating, an indirect measurement of this force will be made using the weight of the static mass as shown and explained below.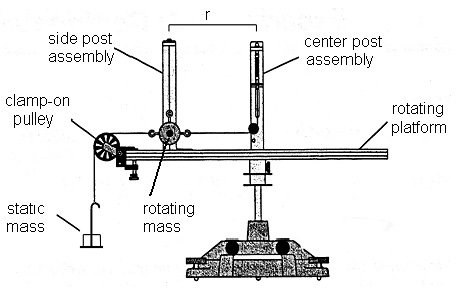
Figure 1
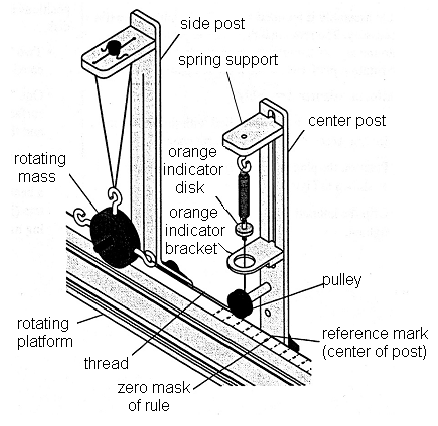
Figure 2
Procedure
Leveling the Apparatus
If the platform is not level, it will adversely affect your results. Students in the first lab of the week should have leveled the apparatus already. Hopefully, the apparatus has not been moved since then and will not need to be leveled again. Check to see if your apparatus is level by turning on the speed control motor and observing the orange indicator disk to see if it bobs up and down as the platform rotates. If your apparatus needs to be leveled, perform the following steps.-
1To roughly level the platform, place a bubble level in the middle of the platform and adjust the two leveling screws on the base of the apparatus until the bubble is centered.
-
2Place some extra mass (~500 g) on the same end of the rotating platform as the rotating mass. If the platform is not level, the heavy end will swing towards the side that is low.
-
3Adjust the leveling screws on the legs of the base until the end of the platform swings uniformly when it is gently rotated by hand.
Setting the Radius
-
1Carefully unhook the rotating mass from its strings. Use a balance to weight it, and record the mass value.
-
2Hang the rotating mass from the side post and connect the string from the spring to the mass. Make sure this string passes under (not behind) the small pulley on the center post.
-
3Move the indicator bracket on the center post to its lowest position.
-
4Pull the rotating mass away from the center post until the orange indicator is centered within the bracket. If the string that supports the rotating mass is not vertical when the indicator is aligned with the bracket, the side post should be moved in or out until the string is vertical. Use the vertical line on the side post to aid in this alignment. When tightening the side post, press down against the platform to assure that it is securely held vertical, and avoid over tightening and breaking the plastic thumb screw!
-
5Measure and record the radius, along with an estimate of uncertainty based on the alignment.
-
6Your apparatus should now be prepared to allow the widest possible range of centripetal forces. (Why is this important?) The centripetal force will be varied by moving the spring support up and down while keeping the other parts of the apparatus fixed in place. This range of motion along the center post should be at least 5 cm, which corresponds to a spring tension range of approximately 1.2 N.
Setting the Centripetal Force Magnitude
In this first part of the procedure, you will use a static (non-rotating) method to adjust the apparatus for a known value of centripetal force.-
1Attach the clamp-on pulley to the end of the platform closest to the rotating mass. Attach a string to the rotating mass and hang a known mass (start with 20 g) over the clamp-on pulley. Adjust the clamp-on pulley up or down as needed so that the string between the pulley and rotating mass is horizontal. (Why is this important?)
-
2Record the value of this static mass, which will determine the centripetal force.
-
3Adjust the spring support vertically until the orange indicator disk is centered in the indicator bracket. The apparatus should now be aligned to precisely know the radius of motion of the rotating mass when the platform is spinning.
Checkpoint 1:
Have your TA check your apparatus before continuing.
Have your TA check your apparatus before continuing.
Measurement of the Period
-
1Remove the static mass and string from the rotational mass. (Why?)
-
2Rotate the apparatus by evenly turning the knurled rod slowly clockwise. Take a minute to get a good feel for turning the platform at a constant speed. Increase the speed until the orange indicator disk is centered in the indicator bracket on the center post. This indicates that the string supporting the rotating mass is vertical and thus the mass is at the desired radius.
-
3As one lab partner rotates the platform the other should use the stopwatch to measure the time it takes to make one revolution. Take ten of these measurements.
-
4An alternative method for measuring the average period is to use a stopwatch to measure the time for N (e.g. 10) revolutions and divide by N to get T. Do this for at least one trial and compare with the value found using the procedure given in step 3. Which method do you think is more accurate?
-
5Before continuing, check your results for this one data point and confirm that your empirical value for the rotating mass is reasonable. If your result does not make sense, analyze your procedure and correct any mistakes before taking additional data.
Checkpoint 2:
Have your TA check your data and calculation results before continuing.
Have your TA check your data and calculation results before continuing.
Vary the Centripetal Force
Repeat the above procedure with at least five different static masses (and therefore, five different forces) that span the widest possible range of values (usually 40 to 150 g).Analysis
-
1The weight of the static mass hanging over the pulley is equal to the centripetal force, F, applied by the spring. Calculate this force for each of your five trials by multiplying the static mass by g and record the results.
-
2For each centripetal force, F, calculate the average period of rotation, T, and its standard error.
-
3For each value F, calculate ω2 and its uncertainty fromω =
.2π T -
4Plot ω2 vs. F (with error bars) and perform a linear least-squares fit.
-
5Determine the experimental value of the rotating mass, m, from the slope of your plot and the centripetal force equation. Identify the y-intercept of the linear fit to your data. Is it what you expect it should be?
