Data Analysis for Physics Labs

You have a number of software options for analyzing your lab data and generating graphs with the help of a computer. Since Microsoft Excel is widely available on all CCI laptops and in ATN computer labs, you are encouraged to use this spreadsheet program to analyze your data. A brief tutorial on using Excel for data analysis is included in this lab manual. Another graphical analysis program called KaleidaGraph is also available, but with limited access (there is not a campus-wide site license for this program). KaleidaGraph is available on the computers in the lab rooms (for your use during lab), in Phillips 245, and in the student computer labs throughout campus (in the physics folder). Instructions for using KaleidaGraph can be found on the lab website. A third software option is PASCO's DataStudio, which is used in the introductory chemistry lab courses and should be available across campus. You may use whichever software program you prefer, but it is your responsibility to ensure that the computational results are correct and consistent with the requirements stated in this lab manual.

No matter which program you use, the section titled Determining the Uncertainty in Slope and Y-intercept may be useful to you.

If you decide to use Excel, you may use the FitHaven templates that accompany the Data Analysis book by William Lichten (this book can be purchased in the campus bookstore, but is not required for this lab). A special license agreement has been obtained from the publisher for UNC-CH physics students to use these templates, which can be downloaded free of charge from the introductory physics lab website. Instructions for using the FitHaven templates are provided with the software, and therefore will not be discussed here. Consult your TA if you have specific questions about analyzing your data using Excel.

Using Excel for Data Analysis

Getting Started

This tutorial will lead you through the steps to create a graph and perform linear regression analysis using an Excel spreadsheet. The techniques presented here can be used to analyze practically any set of data you will encounter in your introductory physics lab. To begin, open Excel from the "Start" menu on your PC (Start > Programs > Microsoft Excel). A blank worksheet should appear. Enter the sample data and column headings shown in Figure 1 into cells A1 through B6. Save the file to a disk or to your personal file space on the campus network. (To do this, click on "File" and choose the "Save As" option.) You will be creating a graph of this data, similar to the one shown in Figure 1.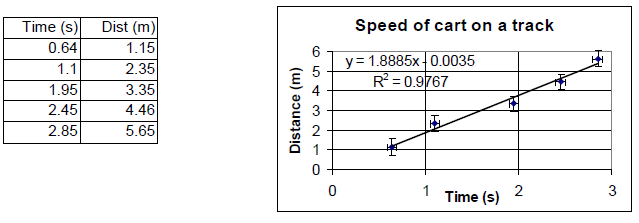

Figure 1

Creating and Editing a Graph

Use your mouse to select all the cells that contain the data that you want to graph. To graph this data, select "Chart" from the "Insert" menu (or click on the "Chart Wizard" icon that should be visible on the toolbar). You will see a series of dialog boxes.

Step 1: Choose "XY (Scatter)" with no lines, and click "Next."

Step 2: This screen allows you to choose which data to plot. Since you did this before starting the Chart Wizard, just click "Next."

Step 3: This screen has multiple menus. Experiment with the settings to see what they do. Make sure your final graph has a descriptive title, axes that are labeled (with units), and no legend. When you are done, click "Next."

Step 4: This screen selects where you will store the graph. Choose "As object in" to store the graph in the same worksheet as the data and click "Finish."

You can move your graph by clicking near its center and dragging. The size can be adjusted by dragging one corner. Most graph features can be modified by double-clicking on the feature you want to change. You can also right-click on a feature to get a menu. Try changing the color of the plot area, the numbers on the axes and the appearance of the data points. It is recommended that you change the background area to white by double-clicking on a blank portion of the graph plot area, and then select "None" under "Area."

Adding Error Bars

Right-click on a data point and choose "Format Data Series..." Click on the "Y Error Bars" tab. Choose "Both" under "Display" and "Fixed Value" under "Error Amount". Then enter the uncertainty for the y-values in the box marked "Fixed Value." You can add "X Error Bars" in a similar manner. Note: Error bars may not be visible if they are smaller than the size of the data marker.

Adding a Trendline

The primary reason for graphing data is to examine the relationship between the two variables plotted on the X- and Y-axes. To add a trendline and display its corresponding equation, right-click on a data point and choose "Add Trendline." Choose the graph shape that best fits your data and is consistent with your theoretical prediction (usually Linear). Click on the "Options" tab and check the boxes for "Display equation on chart" and "Display R-squared value on chart." A good fit is indicated by an R² value close to 1.0.

Caution: When searching for a mathematical model that explains your data, it is very easy to use the trendline tool to produce nonsense. This tool should be used to find the simplest mathematical model that explains the relationship between the two variables you are graphing. Look at the equation and shape of the trendline critically: Does it make sense in terms of the physical principle you are investigating? Is this the best possible explanation for the relationship between the two variables? Use the simplest equation that passes through most of the error bars on your graph. You may need to try a couple of trendlines before you get the most appropriate one. To clear a trendline, right-click on that regression line and select "Clear."

Determining the Uncertainty in Slope and Y-intercept

The R² value indicates the quality of the least-squares fit, but this value does not give the error in the slope directly. However, the standard error (uncertainty) in the slope m can be determined from the R² value by using the following formula:

( 1 )

σ_m = m

R²

− 1

n − 2

where the best fit line is

y = mx + b,

with n data points. The uncertainty in the y-intercept b is the following.

( 2 )

σ_b = σ_m

Σx²

These values can be computed directly in Excel or by using a calculator. For this sample set of data,

σ_m = 0.1684 m/s,

and

σ_b = 0.333 m.

The uncertainty in the slope and y-intercept can also be found by using the LINEST function in Excel. Using this function is somewhat tedious and is best understood from the Help feature in Excel.

Interpreting the Results

Once a regression line has been found, the equation must be interpreted in terms of the context of the situation being analyzed. This sample data set came from a cart moving along a track. We can see that the cart was moving at nearly a constant speed since the data points tend to lie in a straight line and do not curve up or down. The speed of the cart is simply the slope of the regression line, and its uncertainty is found from the equation above:

v = 1.9 ± 0.2 m/s.

(Note: If we had plotted a graph of time versus distance, then the speed would be the inverse of the slope:

v = 1/m)

The y-intercept gives us the initial position of the cart:

x₀ = −0.0035 ± 0.33 m,

which is essentially zero.

Copying Data and Graphs into a Word Document

You can copy graphs and data from Excel to Word. Just select the graph (or cells) and use the "Edit" menu or Ctrl-C and Ctrl-V shortcuts to copy and paste.

Data Analysis with Excel - the easy way!

For quick and easy data analysis with Excel, download the FITHAVEN template that is available from the labs website.