Lesson 6 - Earth and the Moon
Reading Assignment
-
•Chapter 7.1: Overall Structure of Planet Earth
-
•Chapter 7.3: Earth's Interior
-
•More Precisely 7-2: Radioactive Dating
-
-
•Chapter 7.5: Earth's Magnetosphere
-
•Chapter 7.4: Surface Activity
-
•Chapter 7.2: Earth's Atmosphere
-
•Discovery 7-1: The Greenhouse Effect and Global Warming
-
-
•Chapter 8.2: Physical Properties (The Moon)
-
•Chapter 8.8: The Origin of the Moon
-
•Chapter 8.1: Orbital Properties (The Moon)
-
•Chapter 7.6: The Tides
-
•Chapter 8.4: Rotation Rates (The Moon)
-
•Chapter 8.7: Interiors (The Moon)
-
•Chapter 8.3: Surface Features on the Moon and Mercury (The Moon)
-
•More Precisely 8-1: Why Air Sticks Around
-
-
•Chapter 8.5: Lunar Cratering and Surface Composition
-
•Chapter 8.9: Evolutionary History of the Moon and Mercury (The Moon)
Math Notes
Average Surface Temperature of a Rapidly Rotating or a Sufficiently Atmosphered Planet (or Moon)
Read Chapter 7.2.
-
•If a planet (or moon) rotates rapidly, the side facing the sun does not have enough time to heat up too much and the side facing away from the sun does not have time to cool down too much, so both sides of the planet radiate about the same amount of heat into space, cooling the planet.
-
•If a planet (or moon) rotates slowly but has a sufficiently thick atmosphere, the atmosphere will redistribute heat from the side facing the sun to the side facing away from the sun, again resulting in a relatively uniform distribution of surface temperature. So again, both sides of the planet radiate about the same amount of heat into space, cooling the planet.
-
•A = albedo, or average fraction of incoming light that is reflected back into space
-
•d = average distance from the sun
( 1 )
T = (278 K) × (1 − A)1/4 ×
 |
| d |
| 1 AU |
 | −1/2 |
-
•Note: This equation assumes that there is no greenhouse effect. If the planet (or moon) has an atmosphere and it has a greenhouse effect, the average surface temperature will be higher.
-
•Note: This equation also holds for Jovian planets, in which case "surface" refers to the depth at which we can no longer see any deeper (i.e., the cloud tops).
Subsolar Temperature of a Slowly Rotating, Insufficiently Atmosphered Planet (or Moon)
Read Chapter 8.2.
-
•The subsolar point is the point on a planet's (or moon's) surface that is directly below the sun. The subsolar temperature is the temperature at this point.
-
•If a planet (or moon) rotates slowly and does not have a sufficiently thick atmosphere to redistribute heat, the side facing the sun heats up and the side facing away from the sun cools down. Furthermore, this means that only one side of the planet radiates most of the heat into space, which means that the planet cools less than if both sides were radiating heat into space.
-
•A = albedo
-
•d = distance from the sun
( 2 )
T = (393 K) × (1 − A)1/4 ×
 |
| d |
| 1 AU |
 | −1/2 |
Average Density
-
•M = mass of planet (or moon)
-
•R = radius of planet (or moon)
( 3 )
average density = (1 Earth density) ×
| ||||||
|
( 4 )
average density = (5520 kg/m3) ×
| ||||||
|
- Example: The mass of the moon is 0.0123 Earth masses. The radius of the moon is 0.273 Earth radii. What is the average density of the moon?
-
Solution: average density = (5520 kg/m3) ×
= 3340 kg/m30.0123 (0.273)3
Surface Gravity
-
•M = mass of planet (or moon)
-
•R = radius of planet (or moon)
( 5 )
surface gravity = (1 Earth surface gravity) ×
| ||||||
|
- Example: The mass of the moon is 0.0123 Earth masses. The radius of the moon is 0.273 Earth radii. What is the surface gravity of the moon?
-
Solution: surface gravity = (1 Earth surface gravity) ×= 0.165 Earth surface gravity
0.0123 (0.273)2 - Consequently, your weight on the moon is 0.165 × your weight on Earth.
Escape Speed
-
•M = mass of planet (or moon)
-
•R = radius of planet (or moon)
( 6 )
escape speed = (1 Earth escape speed) ×
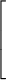 |
| ||||
|
 | 1/2 |
( 7 )
escape speed = (11.2 km/s) ×
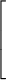 |
| ||||
|
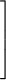 | 1/2 |
- Example: The mass of the moon is 0.0123 Earth masses. The radius of the moon is 0.273 Earth radii. What is the escape speed of the moon?
-
Solution: escape speed = (11.2 km/s) ×

0.0123 0.273
= 2.38 km/s
1/2
Atmospheric Composition
Read More Precisely 8-1.
-
•Consider molecules in a planet's (or moon's) atmosphere. The hotter the atmosphere, the faster the molecules move. Most molecules move near the average molecular speed for a gas of that temperature. But many molecules move slower and faster. If the faster moving molecules are moving in excess of the gravitational escape speed of the planet, they will be lost into space. Eventually, slower moving particles will warm up and take their place, and will also be lost into space. Eventually, nearly all of that type of molecule will be lost into space.
-
•So how fast is too fast? As a rule of thumb, if
( 8 )
6 × average molecular speed > escape speed,
- nearly all of that type of molecule will be lost into space.
-
•T = surface temperature
-
•m = molecular mass, or number of protons plus number of neutrons
( 9 )
average molecular speed = (0.157 km/s) ×
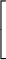 |
| ||||
| m |
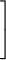 | 1/2 |
-
•Note: This equation also holds for Jovian planets, in which case "surface" refers to the depth at which we can no longer see any deeper (i.e., the cloud tops).
-
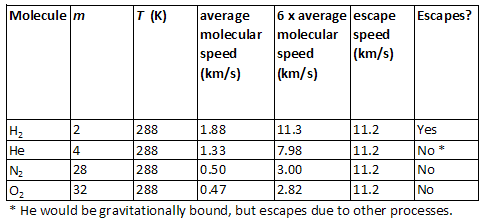
•Example: Earth's average surface temperature is 288 K and its escape speed is 11.2 km/s. The following table shows which molecules escape (lighter molecules, like hydrogen) and which are gravitationally bound (heavier molecules, like nitrogen and oxygen, which make up most of Earth's atmosphere).
-
•Example: The moon's average surface temperature is 227 K and its escape speed is 2.4 km/s. The following table shows which molecules escape (all of them) and which are gravitationally bound (none of them).
Radioactive Dating
-
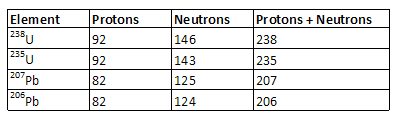
•Some elements are not stable. For example, 238U (uranium) decays to 206Pb (lead) and 235U decays to 207Pb. Uranium has 92 protons and lead has 82 protons. The number in the upper left hand corner is the number of protons plus the number of neutrons.
-
•Consider a sample of 238U. Half of it will decay to 206Pb in 4.5 billion years. This is called the half-life 238U. Half of what's left will decay in another 4.5 billion years, leaving only one quarter of the original sample after two half-lifes. Half of what's left will decay in another 4.5 billion years, leaving only one eighth of the original sample after three half-lifes. And so on.
-
•The half-life of 235U is 0.713 billion years.
-
•Example: Consider a rock where all of the 206Pb came from the decay of 238U. If there are as many 206Pb atoms as 238U atoms, half of the original sample of 238U has decayed, which means that the rock is one half-life, or 4.5 billion years, old.
-
•Note: Radiometric dating is complicated by the fact that not all 206Pb and 207Pb in rocks come from the decay of 238U and 235U, respectively. Consequently, measurements are typically made only in zircon crystals, which form in the rocks when the rocks form. Zircon crystals are unable to incorporate lead atoms into their lattice structure, but are able to incorporate uranium atoms. Consequently, all lead found in zircon crystals must come from the decay of uranium, in which case the age of the zircon crystals, and consequently the age of the rock in which they formed, can be found as above.