3.6 Thermal Radiation
Pre-Lecture Reading 3.6
-
•Astronomy Today, 8th Edition (Chaisson & McMillan)
-
•Astronomy Today, 7th Edition (Chaisson & McMillan)
-
•Astronomy Today, 6th Edition (Chaisson & McMillan)
Video Lecture
-
•Thermal Radiation (27:10)
Supplementary Notes
Thermal Radiation
-
•See Thermal Radiation.
-
•Temperature measures the average motion of a collection of particles.
-
•Absolute zero corresponds to no motion.
-
•Moving particles bounce off of one another.
-
•These bounces create ripples in the electromagnetic fields emanating from these particles.
-
•These ripples are light (see Light and the Electromagnetic Field).
-
•Consequently, a distribution of particle speeds results in a distribution of bounce speeds, and consequently in a distribution of ripple frequencies, and consequently in a distribution of light frequencies.
-
•This distribution of light frequencies is called a Planck, or blackbody, or thermal distribution.
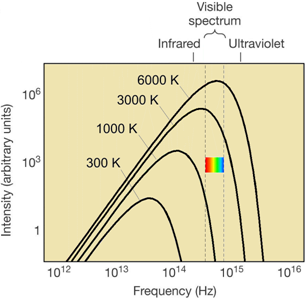
Figure 1
-
•Higher temperatures correspond to faster particle speeds, and consequently faster bounce speeds, and consequently higher-frequency ripples, and consequently higher-frequency light: The distribution of light shifts to higher frequencies. This is called Wien's Law.
-
•Higher temperatures correspond to faster particle motions, and consequently more particle bounces, and consequently more ripples in the electromagnetic field, and consequently more light: The distribution of light becomes more intense at all frequencies. This is called Stefan's Law.
Wien's Law
-
•See Wien's Law.
-
•λpeak = wavelengthat which a blackbody emits the most light
-
•T = temperature of the blackbody
-
•For stars, λpeak is usually measured in nm and T in 1,000s of K. Hence, you might find this equivalent form of Wien's law more convenient to use:
-
•Reminder: The visible part of the electromagnetic spectrum spans wavelengths of ≈700 nm (red) to ≈400 nm (violet).
-
•If λpeak is in the ultraviolet, X-ray, or gamma-ray parts of the electromagnetic spectrum, its thermal distribution will still cross the visible part of the spectrum, and will be blue in color.
-
•If λpeak is in the near-infrared (infrared, but almost visible) part of the electromagnetic spectrum, its thermal distribution will still cross the red side of the visible part of the spectrum, and will consequently be red in color (e.g., the
T = 1,000 distribution in Figure 1). -
•If λpeak is in the far-infrared or radio parts of the electromagnetic spectrum, its distribution will not cross the visible part of the spectrum, and will consequently be invisible (although detectable in the far-infrared and radio; e.g., the T = 300 distribution in Figure 1).
Stefan's Law
-
•See Stefan's Law.
-
•F = energy flux (energy emitted per unit area and per unit time) of a blackbody
-
•σ (Greek letter "sigma") = Stefan–Boltzmann constant
-
•T = temperature of the blackbody
In this course, you will never need to use the Stefan–Boltzmann constant to solve a problem.
Example:
Person A has a fever and is 1.01 times hotter than Person B. The energy flux coming off of Person A is how many times greater than the energy flux coming off of Person B? Solution: Let TA and FA be the temperature and energy flux of Person A. Let TB and FB be the temperature and energy flux of Person B. Then, FA = σTA4 and FB = σTB4. Dividing the latter equation into the former equation yields:
Person A has a fever and is 1.01 times hotter than Person B. The energy flux coming off of Person A is how many times greater than the energy flux coming off of Person B? Solution: Let TA and FA be the temperature and energy flux of Person A. Let TB and FB be the temperature and energy flux of Person B. Then, FA = σTA4 and FB = σTB4. Dividing the latter equation into the former equation yields:
| = |
| ||||||
| = |
| |||||||
| = | 1.014 ≈ 1.04. |
-
•Notice that we did not need to know the constant of proportionality, in this case σ, to solve this problem. This is what is called a ratio problem.
Most of the math problems in this course are ratio problems.
-
•If the constant of proportionality is not needed, we can more simply write:
F ∝ T4
Example:
Person A has a fever and is 1.01 times hotter than Person B. The energy flux coming off of Person A is 1.014 = 1.04 times greater than the energy flux coming off of Person B.
Person A has a fever and is 1.01 times hotter than Person B. The energy flux coming off of Person A is 1.014 = 1.04 times greater than the energy flux coming off of Person B.
Assignment 3
-
•Do Questions 4 and 5.


