Charging and Discharging the RC Circuits

Topics and Files

E&M Topic

RC circuit

DataStudio File

71 RC Circuit.ds

Equipment List

Introduction

The purpose of this activity is to measure the voltage across a capacitor as it is charged and then discharged through a resistor that is in series with the capacitor. Use a voltage sensor to measure the change in voltage across the capacitor. Use the 'Output' feature of the interface to first charge and then discharge the capacitor through the resistor. Calculate the capacitance of the capacitor based on your data and compare to the printed value on the capacitor.

Background

When a DC voltage source is connected across an uncharged capacitor, the rate at which the capacitor charges up decreases as time passes. At first, the capacitor is easy to charge because there is very little charge on the plates. But as charge accumulates on the plates, the voltage source must "do more work" to move additional charges onto the plates because the plates already have charge of the same sign on them. As a result, the capacitor charges exponentially, quickly at the beginning and more slowly as the capacitor becomes fully charged. The charge on the plates at any time is given by:

( 1 )

q = q₀

1 − e^−t/τ

where q₀ is the maximum charge on the plates and τ is the capacitive time constant (τ = RC, where R is resistance and C is capacitance). NOTE: The stated value of a capacitor may vary by as much as ±20% from the actual value. Taking the extreme limits, notice that when

t = 0, q = 0

which means there is not any charge on the plates initially. Also notice that when t goes to infinity, q goes to q₀ which means it takes an infinite amount of time to completely charge the capacitor.

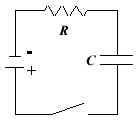
Figure 1

The time it takes to charge the capacitor to half full is called the half-life and is related to the capacitive time constant in the following way.

( 2 )

t_1/2 = RC ln 2

( 3 )

t_1/2 = τ ln 2

In this activity the charge on the capacitor will be measured indirectly by measuring the voltage across the capacitor since these two values are proportional to each other:

q = CV.