Print

Resistance; Ohm's Law

Topics and Files

E&M Topics

  • Ohm's Law
  • Series and parallel circuits

DataStudio Files

  • 67 Ohm's Law.ds
  • 69 Resistors.ds

Equipment List

Introduction

This lab has two parts. The purpose of Experiment 1 is to confirm the relationship of current, voltage, and resistance in an electric circuit. You will also explore what happens to the resistance of a light bulb's filament as it changes temperature. Use the DataStudio software to measure the current through resistors and the filament of a light bulb as the voltage across the resistors and the filament of the light bulb is changed. The purpose of Experiment 2 is to confirm that when resistors are added in series to a circuit, they have a total resistance that equals the sum of their individual resistances, and that when resistors are added in parallel to a circuit, they have a total resistance that is less than the individual resistances. Use a voltage sensor, a current sensor, and the DataStudio software to measure the voltage across parts of the series and parallel circuits, and a current sensor to measure the current through the circuits.

Background

Ohm discovered that when the voltage (potential difference) across a resistor changes, the current through the resistor changes. He expressed this as
( 1 )
I =
V
R
 
where I is current, V is voltage (potential difference), and R is resistance. Current is directly proportional to voltage and inversely proportional to resistance. In other words, as the voltage increases, so does the current. The proportionality constant is the value of the resistance. Since the current is inversely proportional to the resistance, as the resistance increases, the current decreases. A resistor is 'Ohmic' if as voltage across the resistor is increased, a graph of voltage versus current shows a straight line (indicating a constant resistance). The slope of the line is the value of the resistance. A resistor is 'non-Ohmic' if the graph of voltage versus current is not a straight line. For example, if resistance changes as voltage changes, the graph of voltage versus current might show a curve with a changing slope. For a certain resistor, the value of its resistance does not change appreciably. However, for a light bulb, the resistance of the filament will change as it heats up and cools down. At high AC frequencies, the filament doesn't have time to cool down, so it remains at a nearly constant temperature and the resistance stays relatively constant. At low AC frequencies (e.g., less than one hertz), the filament has time to change temperature. As a consequence, the resistance of the filament changes dramatically and the resulting change in current through the filament is interesting to watch. In the first part of this activity, investigate the relationship between current and voltage in simple ten-ohm (Ω) and one-hundred ohm resistors. In the second part, investigate the relationship between current and voltage in the filament of a small light bulb. In a series circuit, devices are connected in such a way that there is the same electric current, I, through each device.
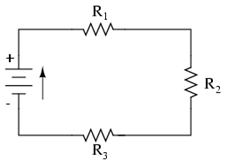
Figure 1

Figure 1

The voltage, V, supplied by the source is divided among the devices. Each device has a resistance, R, that is the ratio of the voltage across the device divided by the current through the device
R =
V
I
.
 Since each device shares a portion of the voltage, V, the following describes how the voltage, current, and individual resistances are related in a series circuit:
( 2 )
V = V1 + V2 + V3 = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRTotal 
where
RTotal
 is the sum of the individual resistances. Components in a series circuit share the same current.
( 3 )
ITotal = I1 = I2 =    In 
Total resistance in a series circuit is equal to the sum of the individual resistances.
( 4 )
RTotal = R1 + R2 +    Rn 
Total voltage in a series circuit is equal to the sum of the individual voltage drops.
( 5 )
VTotal = V1 + V2 +    Vn 
In a parallel circuit, devices are connected in such a way that the same voltage is supplied across each device.
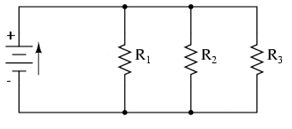
Figure 2

Figure 2

When more than one device is connected in parallel to a voltage source, each receives current from the source as if the other device were not there. Therefore, two devices connected in parallel draw more current from the source than either device does by itself. The following describes how the voltage, current, and individual resistances are related in a parallel circuit.
( 6 )
I = I1 + I2 + I3 =
V
R1
+
V
R2
+
V
R3
= V
1
R1
+
1
R2
+
1
R3
= V
1
REquivalent
 
You can calculate the value of
REquivalent
 from the other individual resistances as follows.
( 7 )
REquivalent =
1
1
R1
+
1
R2
+
1
R3
+   
 
Components in a parallel circuit share the same voltage.
( 8 )
VTotal = V1 = V2 =    Vn 
Total resistance in a parallel circuit is less than any of the individual resistances.
( 9 )
RTotal = 1/(1/R1 + 1/R2 +    1/Rn) 
Total current in a parallel circuit is equal to the sum of the individual branch currents.
( 10 )
Itotal = I1 + I2 +    In 

Copyright © 2011-2013 Advanced Instructional Systems, Inc. and the University of Central Florida Physics Department | Credits