Simple Pendulum

Introduction

Simple Pendulum

A simple pendulum consists of a large mass (bob) suspended by a light string from a rigid support (Figure 1). The length of the string is large compared to the dimensions of the bob. A stationary pendulum has its string in a vertical position with the bob hanging straight down. This is known as the pendulum's equilibrium position (since if left undisturbed, the pendulum will remain in this position). Oscillations (to and fro motion) are set up in a pendulum by displacing the bob from its equilibrium positions and releasing it.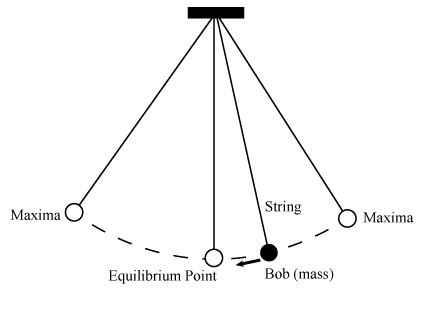

Figure 1: Simple pendulum

The period of the pendulum is the time required for the pendulum bob to complete one oscillation (cycle). One oscillation is the motion of the pendulum beginning at some reference point and continuing until the reference point is reached again (and the motion starts to repeat itself). The reference points that we will use are the equilibrium point and one of the two maxima (points of maximum displacement from equilibrium). Note that in one cycle the bob reaches the equilibrium point twice, once while traveling to the left and once while traveling to the right.

Measurements, Mean and Standard Deviation

Due to inaccuracy in measuring any physical quantity, different measurements of the same quantity do not necessarily yield identical results. Having obtained n measurements T₁, T₂, ..., T_n for a quantity T, the results are often presented in the form

( 1 )

T = T_mean ± ΔT,

where

( 2 )

T_mean =

T₁ + T₂ + ... + T_n

is the arithmetic mean or average of the measurements and

( 3 )

ΔT =

(T₁ − T_mean)² + (T₂ − T_mean)² +

+ (T_n − T_mean)²

n − 1

is the standard deviation of the set of measurement results. (See the Appendix.) ΔT gives a measure of how much the measurements were spread out. If ΔT is large, the measured values were quite different from each other. Sometimes ΔT is called the random uncertainty of T. The "real value" of T has a 68% probability of being within ΔT of T_mean. In this experiment we will measure the period of the simple pendulum using a stopwatch. Two different approaches for making the measurement will be used. We will also measure the period for a pendulum with a bob of a different mass to explore the dependence of the period on the mass of the bob. For each set of measurements we will determine the average period and the standard deviation.

Objective

This experiment explores the treatment of measurement error and tests if the period of a simple pendulum depends on the mass of the bob. This experiment also serves as an introduction to WebAssign.

Apparatus

Stopwatch
One pendulum with a heavy mass and one with a light mass (one setup at the front of the room)

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Experiment A

The instructor will set the pendulum with the lighter mass in motion and one person from each lab group will time one period. Make sure your stopwatch is at zero and wait until the pendulum has moved at least two cycles before starting the stopwatch. This ensures that the pendulum has had enough time to settle into steady motion. Use the equilibrium position as the reference point for determining the beginning and ending of the cycle. The instructor will ask for the result from each group and will write the data from each group on the whiteboard at the front of the room. Input the measurements of the time for one period done by each group into Table 1 on your worksheet. If there are 12 lab groups present, the table should have 12 entries.

What is the number of entries (the number n of measured values) in Table 1?

Calculate the average value of the period. (It is suggested that you use Excel to do this and subsequent calculations.)

Calculate the standard deviation.

Experiment B

Pass the stopwatch to the other member of your lab group. Repeat Experiment A with the same pendulum but now take one of the maximum positions of the bob as the reference point. Input the measurement of the time for one period from each group into Table 2 on your worksheet.

What is the number of entries (the number n of measured values) in Table 2?

Calculate the average value of the period.

Calculate the standard deviation.

Experiment C

The stopwatch should be passed back to the first lab partner. Repeat Experiment B, but now with the pendulum that has the heavier mass. As in Experiment B, use one of the maximum positions of the bob as the reference point. Input the measurement of the time for one period from each group into Table 3 on your worksheet.

What is the number of entries (the number n of measured values) in Table 3?

Calculate the average value of the period.

Calculate the standard deviation.

Analysis

Discuss the following questions with your lab partner.

Do your values of T_{B, mean} or T_{C, mean} agree to within ΔT_B and ΔT_C? Do your results therefore support or disprove the hypothesis that the period of a simple pendulum is independent of the mass of the bob?

Does one choice of reference point give a smaller ΔT than the other choice?