Photoelectric Effect

Introduction

The photoelectric effect is the emission of electrons (called photoelectrons) from the surface of a conductor when light shines on the surface. The energy of a photon is given by

( 1 )

E_photon = hf =

where we have used the wave relation

c = fλ.

The constant h is called Planck's constant. In the photoelectric effect light of wavelength λ falls on a metal surface. A photon is absorbed and all of the photon energy is transferred to an electron in the metal. The minimum energy required to free an electron from the surface of the metal is called the work function ϕ. Conservation of energy gives

( 2 )

hf = K_max + ϕ

where K_max is the maximum kinetic energy of the electrons emitted by the surface. Electrons from the interior of the metal can also be ejected but they require more energy than ϕ to be released from the metal and therefore have less kinetic energy than K_max. The rate at which photoelectrons are produced can be determined by collecting them at a metal anode and measuring the resulting current. The value of K_max can be measured by imposing a potential barrier, V, that converts part of the kinetic energy of the electrons to electric potential energy, eV. The stopping potential, V₀, is the value of V for which all the kinetic energy is removed, so

eV₀ = K_max

and the conservation of energy equation for the photoelectric effect becomes

( 3 )

hf = eV₀ + ϕ.

This model for the photoelectric effect predicts a threshold frequency f_th that is the minimum frequency the light must have in order to produce any photoelectrons. The threshold frequency is calculated by setting

K_max = 0

in the energy conservation equation and this gives

( 4 )

f_th =

The threshold frequency corresponds to a maximum wavelength

( 5 )

λ_max =

f_th

If the wavelength of the light is greater than λ_max no photoelectrons are produced.

Objective

In this lab we will analyze photoelectric data in order to calculate the work function of the surface, the value of Planck's constant, h, and the threshold frequency.

Apparatus

In-lab computers
Excel

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Data

The following data is an example of measured stopping potential, V₀, as a function of the wavelength, λ, of the light.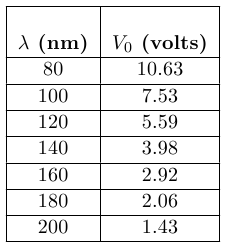

Table 1

Note: You will be given a different set of data in the WebAssign question.

In analyzing this data use the following values for physical constants:

1 eV = 1.602 × 10⁻¹⁹ J,

e = 1.602 × 10⁻¹⁹ J,

and c = 2.998 × 10⁸ m/s.

Analysis

Find the frequency f (in Hz) for each value of the wavelengths in the data table and use Excel to plot V₀ in volts (vertical axis) versus f in Hz (horizontal axis). You can use a formula in Excel to calculate f from λ.

Use Excel to find the best straight-line fit to the data.

Record the slope and y-intercept of this line. Be sure to include the correct units and use three significant figures.

You can control the number of significant figures displayed in the equation for the line as follows.

1
Right-click on the trendline equation.
2
Select Format Trendline Label.
3
Select Scientific with 2 decimal places.

Use the y-intercept value from Excel to calculate the work function, ϕ, in electron volts and record your result.

Use the slope from Excel to calculate the value of Planck's constant, h. Express your result in J · s.

Use the value of the work function calculated from the data to determine the threshold frequency in Hz for the surface. In this calculation use the value of h that you obtained in the previous step. Or, you can use the equation from your Excel graph to find the value of f that gives

V₀ = 0.

Use the threshold frequency from the previous step to calculate the maximum wavelength of light in nm that will produce photoelectrons from this surface.