Investigating Springs (Simple Harmonic Motion)

Introduction

The purpose of this lab is to study the well-known force exerted by a spring. The force, as given by Hooke's Law, is a function of the amount the spring is stretched or compressed and therefore the constant force formulae and resulting trivial potential energy functions do not apply. The motion of an object suspended from an ideal spring, in the absence of any friction, is called Simple Harmonic Motion. This type of motion occurs in a wide variety of physical systems and is itself worth studying. You can also obtain the potential energy function for the spring force and test the Law of Conservation of Energy. Everything seems to work out exactly as expected. However, when the force of the spring is investigated as a function of the mass of the object suspended from it, there is a puzzling result.

Determining the Spring Constant

When a mass, m, is suspended from a spring the extension of the spring at the equilibrium position can easily be measured. From the free body diagram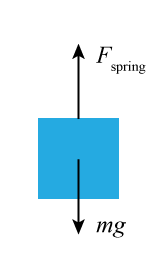

Two arrows of equal length point outward from a square. The arrow labeled F sub spring points upward and has its tail at the top of the square. The arrow labeled m g points downward and has its tail at the center of the square.

Figure 1

and Newton's second law, with the mass at rest,

( 1 )

ΣF = 0,

you have,

( 2 )

F_spring = mg.

Assuming that the force of the spring is given by Hooke's Law, which states that the magnitude of the force is a constant times the amount the spring is stretched or compressed, we have

( 3 )

F_spring = −kx_eq = mg.

Here

x_eq

is the extension of the spring at equilibrium (note: a downward stretch is a negative displacement), k is called the spring constant and from the above we have

( 4 )

k = −

x_eq

Conservation of Energy and Simple Harmonic Motion

We have seen in lecture that the spring force is a conservative force like gravity and as a result can be represented by a potential energy function

( 5 )

U_spring =

kx² + C_spring

( 6 )

U_gravity = −mgx + C_gravity

where x is the displacement measured from the springs equilibrium position and the C's are arbitrary constants. Then using the Work-Energy Theorem, the total energy of a moving mass on the end of a spring in the presence of a uniform gravitational acceleration is given by

( 7 )

ΔKE = ΔU_gravity + ΔU_spring

( 8 )

mv(x)² = mgx −

kx².

If we start such a mass moving about its equilibrium position, we see that the mass will undergo a repetitive oscillation until these oscillations gradually die away and the object is once again at the equilibrium position. This motion as noted above is often described as Simple Harmonic Motion. During these oscillations, we observe that the period of the oscillations remains approximately constant despite the fact that the oscillations are gradually dying away. If we investigate this system of mass and spring further using Newton's Laws, we can write down the equations of motion for this mass undergoing these oscillations and we find the following.

( 9 )

mg − kx = ma_x = m

d²x

dt²

The details of solving this equation will be discussed in the text and lecture, however from our observation of this system undergoing these oscillations, we appreciate that the solutions must be some form of oscillatory functions like sine and cosine of ωt. If we set the origin of our coordinate system at the equilibrium position of the mass on the end of the spring when it is at rest, we can then write down the solution of this equation as

( 10 )

x(t) = A sin(ωt) + B cos(ωt)

where

( 11 )

ω =

k/m

and the period of these oscillations is given by

( 12 )

T =

2π

k/m

To see that this function does indeed satisfy the equations of motion, substitute it into the equation and see what results. Note, in these calculations, we have assumed that the mass of the spring is negligible, however, if we allow the spring to have a mass and do the calculus necessary to solve the modified equation of motion, we find that the period of oscillation is modified as follows

( 13 )

T_{real spring} =

2π

m + m_effective

where the effective mass of the spring is

m_eff =

m_spring

Objectives

In this lab, you will investigate the properties of a simple mass-spring system,

1
to make static measurements of the spring constant and the dependence of the stretch of the spring from equilibrium to the force being applied to it,
2
then to make dynamic measurements of the mass and spring system while oscillating to investigate simple harmonic motion in this system,
3
and lastly, observe the effect of the spring mass on the period of the Simple Harmonic Motion.

Apparatus

Electronic stop clock
Mass holder
Slotted mass set
Spiral spring
Support rod and base
Ruler (taped to support rod)
Balance

A stop clock and a vertical stand are placed on a table. A ruler runs along the vertical stand and is taped to it. At the top of the stand is an eye-bolt affixed horizontally. A mass holder with slotted masses is held vertically in the air by a spring attached to the eye-bolt. Additional, available slotted masses lie on the table.

Figure 2

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Method I: Static Measurements

Hang the spring from the eye-bolt at the top of the support rod. Hook the mass holder onto the bottom end of the spring and if necessary add enough slotted masses to the mass holder to just separate the coils of the spring. Observe the position of the bottom of the mass holder on the ruler. Call this value y₀ and record its value.

Now add additional mass, ΔM, to the mass hanger and let the mass hang at rest. Do this for each value of ΔM given in Table 1. Note the position, y, on the scale of the bottom of the mass holder. The change in length, Δl, of the spring in each case is

y − y₀.

Record your measured values of y for each ΔM in Table 1 and enter the quantity

Δl = y − y₀.

Note that in Table 1 ΔM is in grams and Δl is in cm. Convert your values of ΔM to kg and your Δl to meters and record in Table 2.

Open Excel and plot the data in Table 2, with Δl on the vertical axis and ΔM on the horizontal axis. Use Excel to find the slope of the straight line that best fits your data.

According to the equation

k(Δl) = g(ΔM),

the vertical intercept of the line should be zero. If the vertical intercept of your line is not small or if your data does not fall close to a straight line, you have made an error in measuring, recording or plotting your data. If this is the case and you and your lab partner can't find what is wrong, ask your lab TA for help.

Record the numerical value of the slope of the line in your Excel graph.

Using

g = 9.80 m/s²

and the slope of the line, calculate k, the force constant of the spring. Since this value of k was determined using Method I, we will call it k_I.

Method II: Dynamic Measurements

Use the balance to measure the mass of the mass holder and record your value.

Hang the mass holder from the lower end of the spring and place a 40 gram slotted mass on the mass holder. Enter the total mass, M, the mass of the slotted mass plus the mass of the holder, in column 2 of Table 3. In column 3 enter the total mass converted to kg.

Displace the mass by about 3 cm downward from the equilibrium position and release to initiate Simple Harmonic Motion. Choose a reference point (the lowest point in the motion works well) and start the stop clock as the bottom of the loaded mass hanger moves past this point.

Start counting with zero (not one) when the stop clock starts and count each time the load passes the reference point, going in the same direction.

Stop the stop clock when 10 oscillations have been completed. Enter this time as t₁₀₍₁₎ in column 4 of Table 3. Repeat the measurement with the other lab partner starting and stopping the stop clock. Enter this time as t₁₀₍₂₎.

Calculate T, the period, as

T =

t₁₀₍₁₎ + t₁₀₍₂₎

and enter into the table.

Repeat the measurements and entries into Table 3 for each value of the slotted mass on the holder that is given for the rows of the table.

Open Excel and plot T (in seconds) versus M (in kg). Does your data fall close to a straight line?

Now plot T² (in s²) versus M (in kg).

Your data should fall close to a straight line. If it doesn't, then you have made an error in measuring, recording or plotting your data. If this is the case and you and your lab partner can't find what is wrong, ask your lab TA for help.

Use Excel to calculate the slope of the straight line that is the best fit to your data and record that value.

Use the slope of the line in your Excel graph to calculate the force constant of the spring. Note that the calculation doesn't require knowing the value of g, the acceleration due to gravity at your location. Since this value of k was determined using Method II, we will call it k_II.

The force constant of the spring has been measured two different ways. The average value of the two results is

k_av =

k_I + k_II

The percentage difference in the two values is given by

% diff =

|k_I − k_II|

k_av

× 100%.

Record the percentage difference for your two values of k. If you have been careful with your measurements and if you have done the analysis correctly, the percentage difference between your two values of k should be less than 10%. If this is not the case, look over what you have done and ask your TA for help if you can't find where you went wrong.

Determining the Effect of Using a Real Spring

Note that our original calculation of the period depended only the mass hanging on the spring, so as the mass goes to zero so should the period. Take a look at your data and observe what the y-intercept of the T² versus M graph is for your Dynamic Measurements. (The y-intercept is the value of T² when M = 0.) Record the value of the y-intercept.

Remember in our equations of motion for the spring and mass, we did not include the mass of the spring, assuming that it was a massless, ideal spring. However, if we allow the spring to have mass, we must add an effective mass for the spring to the mass on the end of the spring to solve these equations fully. This added spring mass alters the expression for the period as follows,

T = 2π

M + m_eff

For a typical spring m_eff is given by

m_eff =

m_spring

where m_spring is the mass of the spring.

For the graph of your data for T² versus M in your dynamic measurements, what does Excel give for the y-intercept of the straight line that best fits your data?

From the value of the y-intercept and the value of the force constant k from Method II, calculate m_eff (the effective mass of the spring).

Use the balance to measure the mass m_spring of the spring. Calculate

m_spring

Recall that the percentage difference between two quantities is the magnitude of their difference divided by their average, converted to a percentage. Calculate the percentage difference between your results for m_eff and

m_spring

This is a measure of how well your measured value of m_eff agrees with the theoretical value of

m_spring