Elastic Collisions: Conservation of Momentum and Mechanical Energy

Introduction

When two bodies collide, a small amount of energy is expended due to the deformation of the bodies. If the collision is elastic, all the energy expended in changing the shape of the objects is recovered. In the case of a perfectly elastic collision, the kinetic energy of the total system containing all the objects remains constant. In this experiment the conservation of momentum and the conservation of kinetic energy will be examined for an elastic collision.

Conservation of Momentum

In any collision, momentum is always conserved. Kinetic energy may or may not be conserved, depending on the nature of the objects involved. Perfectly elastic collisions can take place between atoms and subatomic particles but on a macroscopic scale, for objects of ordinary size, perfectly elastic collisions do not occur. However, if the objects involved in the collisions are sufficiently rigid, then the amount of kinetic energy lost is very small and the collision, for all practical purposes can be considered elastic. When a particle of mass, m, moving with a velocity, v_1i, collides with a second particle of the same mass that is at rest, the conservation of momentum gives

( 1 )

mv_1i + m(0) = mv_1f + mv_2f

where v_1f and v_2f are the velocities of the two masses after the collision. If the collision is elastic, then the conservation of kinetic energy can be invoked and

( 2 )

m|v_1i|² +

m(0)² =

m|v_1f|² +

m|v_2f|².

For a head-on collision (see Figure 1), all the momentum and all the kinetic energy of the first particle is transferred to the second and the first particle has a zero velocity after the collision. In this case the two conservation equations result in

( 3 )

mv_1i + 0 = 0 + mv_2f

( 4 )

v_1i = v_2f

( 5 )

m|v_1i|² + 0 =

m|v_2f|²

( 6 )

|v_1i|² = |v_2f|².

So for a head-on collision, the velocity of particle 2 after the collision is equal in magnitude and is in the same direction as the velocity of particle 1 before the collision.

A circle labeled m_1 has an arrow pointing to the right at another circle labeled m_2. The arrow is labeled v_1i. Above the circle m_2 is the text v_2i = 0. To the right of this diagram is another diagram with circle m_1 and the text v_1f = 0 above. To its right is the circle m_2 with an arrow pointing to the right labeled v_2f.

Figure 1: Head-on collision

If the collision is a glancing collision (see Figure 2), only part of the energy and momentum of particle 1 is transferred to particle 2. In this case, conservation of energy and momentum result in

( 7 )

mv_1i + 0 = mv_1f + mv_2f

( 8 )

v_1i = v_1f + v_2f

( 9 )

m|v_1i|² + 0 =

m|v_1f|² +

m|v_2f|²

( 10 )

|v_1i|² = |v_1f|² + |v_2f|².

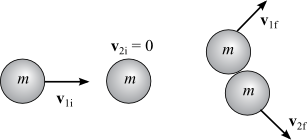
A circle labeled m_1 has an arrow pointing to the right in the direction of another circle labeled m_2. The arrow is labeled v_1i. Above the circle m_2 is the text v_2i = 0. To the right of this diagram is another diagram with circle m_2 touching and directly above circle m_1. Extending diagonally down and to the right from m_1 is an arrow labeled v_1f. Extending diagonally up and to the right from m_2 is an arrow labeled v_2f.

Figure 2: Glancing Collision

Suppose the collision between the two particles occurs at some height above the ground and that after the collision the particles are allowed to fall. When the two particles are at the same height, if the initial velocity of particle 1 is horizontal and particle 2 is initially at rest, then immediately after the collision the velocities of the two particles will still be in the horizontal direction. The horizontal position of the particles as they follow a trajectory to the ground will be given by

( 11 )

x(t) = x(0) + v_xi(0)t

( 12 )

x₁(t) = v_1ft

( 13 )

x₂(t) = v_2ft

( 14 )

v_1f =

x₁(t)

( 15 )

v_2f =

x₂(t)

The velocities of the two particles therefore are proportional to the horizontal distance they travel after the impact. Since the particles are at the same height when they collide, the fall time, t, is the same for both and a measurement of

x(t)

provides all the information necessary to examine the conservation of momentum and kinetic energy. (While we have noted that the time of fall is the same for all of the spheres and therefore can be factored out of your calculations, you should be able to calculate the time of fall for these spheres from your knowledge of the motion of a freely falling body under the influence of gravity.)

Objectives

In this lab you will perform both "head-on" and "glancing" collisions using two steel spheres. By measuring the horizontal distances that they travel after the collision, you will be able to measure their velocities and then find their kinetic energy and momentum before and after the collisions. Once you have made these calculations you will use your data to test the laws of conservation of momentum and mechanical energy in these collisions.

Apparatus

Grooved track
Two steel balls
Large sheet of paper (2' × 2')
Carbon paper (2 pieces - 6" × 6")
Meterstick
Protractor
Compass

An L-shaped piece of wood is clamped down to the top of the table. A metal track is attached to the top of the vertical part of the wood and slopes down to the horizontal part of the wood to where it extends slightly off the edge of the table. A stop at the top of the track ensures balls are always launched at the same position. A steel ball sits on a stand just in front of the bottom of the track. A chain hangs down from this stand to the floor.

Figure 3

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

The elastic collision apparatus consists of a grooved track mounted on a wooden base. One of the steel balls (called the projectile since it will be projected along the track) is held against a small metal stop at the upper end of the track until it is ready to be released. At the lower end of the track is a movable target support that will hold the second steel ball (the target ball). The horizontal and vertical positions of the screw can be adjusted to allow for glancing, head-on and no collisions.

Tape a large (2' × 2') piece of paper to the floor near the table so that it is centered under the apparatus and extends several inches back under the edge of the table.

Be sure that the paper and the table do not move during the experiment.

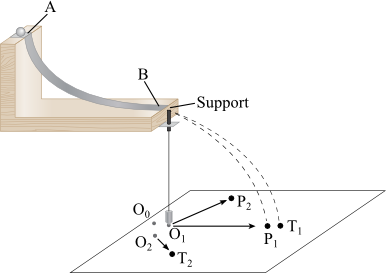
A ball starts at a position A on a track connected to a vertical block on top of a table. The track slopes down, connecting to the top of a horizontal block where it ends just over the edge of the table to a position labeled B. On the floor in front of everything is a square sheet. Two dotted lines show the path of two balls that have fallen off the track on the table and onto the sheet on the floor. A point labeled P_1 represents a ball that lands slightly closer to the table than a ball's impact point labeled T_1. A chain with a small weight hangs down from the end of the track to the square sheet. Beneath the weight are three dots arranged in an upside down triangle on the sheet. The top left dot is labeled O_0. The top right dot is labeled O_1 and from it extends a medium length arrow to a point labeled P_2. A longer arrow extends also from O_1 to the right to a point labeled P_1. The bottom dot is labeled O_2 and from it extends a short arrow to the bottom right to the ball's impact point labeled T_2.

Figure 4

A: Determining the Initial Velocity of the Projectile (No Collision)

Take one of the steel balls and hold it at the top of the grooved track at point A (Figure 4). This is the projectile. Loosen the lock nut on the target support and move it to the side so that the projectile will not strike the support as it leaves the track and falls to the floor. Release the projectile and note where it strikes the paper that was placed on the floor. Place a piece of carbon paper facedown at the approximate point where the projectile landed. Release the projectile from the top of the track six times. Be sure it strikes the carbon paper and leaves a mark on the paper underneath each time.

Remove the carbon paper and surround the six dots with a very lightly drawn circle and draw a line through each dot to indicate that they are associated with this data set. The circle does not need to be exact, it will only be used to temporarily distinguish these marks from those made later in the experiment. Label this set of points P₁.

B: Head-on Collision

A steel ball is near the bottom edge of a horizontal metal track. Just to the left of the edge of the track is another ball sitting atop a screw. This ball is at the same height as the horizontal track.

Figure 5

Move the target support so that it is directly in the path of the projectile (Figure 5).

a
The support must be centered exactly along the axis of the track and not moved to one side or the other.
b
Place one steel ball, the target ball, on the support and place the projectile as close as possible to the end of the track.
c
In order to obtain a head-on collision, the two balls must be at the same height when they collide. Adjust the target support until the two balls are at the same height.
d
In addition, the projectile must strike the target just as the projectile leaves the track. This means that the target support should be adjusted so that the two balls are touching when the projectile is just resting on the edge of the track.
e
Check once again that the two balls are at the same height and are aligned along the axis of the track.
f
Clamp the target support in place by tightening the lock nut under the target support.

Place the target on the support. Release the projectile from point A and note where the target lands after the collision. It should fall at a point at or just beyond P₁. If it lands too short or too much to the side, check the alignment of the target support once more to be certain that the collision is head-on.

Place the carbon paper facedown. Place the target on the support and release the projectile from point A. Do this six times. Remove the carbon paper and lightly circle the six new points for the head-on collision, placing an X on center of each of the impact points. Call this grouping T₁.

In order to indicate the position of the target before the collision, lower the plumb bob on the target support until its point almost touches the paper. Put a mark on the paper directly under the plumb bob. Darken this point with a pen or pencil if necessary and label it O₁.

C: Glancing Collision

For the glancing collision, the target support should be moved to one side so that the projectile, when released, will just barely strike the target.

a
Place the target on the support and release the projectile from point A.
b
Note where the two balls land (do not use the carbon paper yet). Adjust the target support until the target has about one-half the horizontal range as the projectile (as seen on the paper).
c
The target holder should still be adjusted so that the two balls are at the same height.
d
Again the two balls should be touching when the projectile is at the edge of the track and is just about to leave it.
e
Tighten the lock nut on the target support once it has been properly aligned.

Place two sheets of carbon paper on the large sheet of paper where the target and the projectile land. Place the target on the support and release the projectile from point A.

Lightly circle each set of points for the glancing collision. Label the points made by the target ball as T₂ and the points made by the projectile as P₂.

Use the plumb bob as before to locate the position of the center of the target during the glancing collision. Label the point located by the plumb bob as O₂.

Have the lab instructor check the large sheet of paper before it is removed from the floor.

Replace the two steel balls in their holders and remove the large sheet of paper from the floor. Be sure to remove any masking tape left on the floor.

D: Data Analysis

Using the compass provided, draw a circle about the points labeled P₁, T₁, P₂, and T₂. The circles should be as small as possible yet still enclose all of the points. Clearly indicate the center of each circle. The radius of each circle will be a measure of the uncertainty (Figure 6).

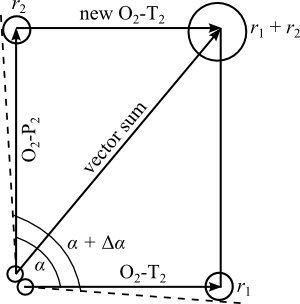
A rectangle has a medium-sized circle centered on the top left corner labeled r_2. A larger circle labeled r_1 + r_2 is centered on the top right corner. A medium-sized circle labeled r_1 is centered on the bottom right corner. The top side has an arrow pointing to the right labeled new O_2 T_2. The left side has an arrow pointing up labeled O_2 P_2. The bottom side has an arrow pointing to the right labeled O_2 T_2. The bottom left corner is composed of two small circles. One circle is slightly down and right of the other and is connected to the bottom side of the rectangle. A dotted line extends from its middle to the bottom edge of r_1. The other circle is connected to the left side of the rectangle. A dotted line extends from its middle to the left edge of r_2. A diagonal line labeled vector sum connects this circle to the center of r_1 + r_2. A small arc labeled alpha connects the sides of the rectangle. A larger arc labeled alpha + delta alpha connects the dotted lines together.

Figure 6

Head-on Collision

Draw a straight line from point P₁ (no-collision) to point O₁, and extend it back 1.27 cm (the diameter of one steel ball) past O₁. Label this point O₀. This is the position of the center of the projectile when it is on the very edge of the track and just about to strike the target.

Using the meterstick, measure and record the length of O₀–P₁. Measure and record the length of O₁–T₁. Measure and record the uncertainties of each of these lines.

Determine and record the difference (and its uncertainty) in the lengths of the lines O₀–P₁, and O₁–T₁. Record the angle between O₀–P₁ and O₁–T₁, as the difference in direction for the two vectors.

Glancing Collision

Draw the lines O₀–P₂ and O₂–T₂. Measure and record the lengths and the uncertainties in the lengths of these two lines.

Measure and record the angle, α(P₂–O₀–T₂), between the lines O₀–P₂ and O₂–T₂. Using the error circles, determine and record the angle

α + Δα.

Add the two vectors produced by the glancing collision by drawing the vector O₂–T₂ at the tip of O₀–P₂. Use the angle, α, and the length measured in step 6.

Draw a line connecting O₀ to the tip of the vector (the new O₂–T₂ just drawn). This is the vector sum of O₀–P₂ and O₂–T₂.

Measure and record the length of the vector sum. Determine and record the error associated with the vector sum. Determine the difference in the lengths (and its uncertainty) for the vector sum and O₀–P₂. Record the difference in direction of the vector sum and O₀–P₂.

E: Questions

According to Equations (11-15), the velocities of the target and the projectile in a collision are proportional to the horizontal range of each. This range is represented by the vectors drawn on the large sheet of paper in the vector analysis section of the procedure. So when the velocities are used to determine whether the momentum and the kinetic energy are conserved, a comparison of the range vectors will provide all the necessary information. For example, if two vectors on the paper have the same length, then the magnitudes of the velocities were equal. Likewise, if two distance vectors have the same orientation, then the two velocities also had identical directions. In answering the following questions, be sure to include equations and to use the numerical results from the vector analysis to support your answers. Include units and uncertainties for all quantities.

Comparing your measurements from the "no collision" data and the "head-on" data, was momentum conserved (to within experimental uncertainty) in the "head-on" collision? See Equations (3) and (4).

Was kinetic energy conserved (to within experimental uncertainty) in the head-on collision? See Equations (5) and (6).

Comparing the "no collision" data with that from the glancing collision,was momentum conserved (to within experimental uncertainty) in the glancing collision? See Equations (7) and (8).

Was kinetic energy conserved (to within experimental uncertainty) in the glancing collision? See Equations (9) and (10).