Geometrical Optics

Introduction

In this experiment, the optical characteristics of mirrors, lenses, and prisms will be studied based on using the following physics definitions and relationships plus simple geometry. If you would like to learn more about the subject of geometrical optics, please consult your text.

Wave Fronts and Rays

In this lab we will use both the concept of a wave front and ray for the propagation of light through a uniform isotropic medium. If we have a point source of light emitting in all directions, we can visualize this disturbance propagating from the source point as a sequence of expanding spheres centered on this point. We call the locus of points located on this wave disturbance with the same phase of vibration a wave front. In Figure 1 below, we illustrate this concept by drawing a line on the wave at the peak of the wave disturbance and show how these curves form a set of concentric spheres that expand with the velocity of propagation of the wave in the medium.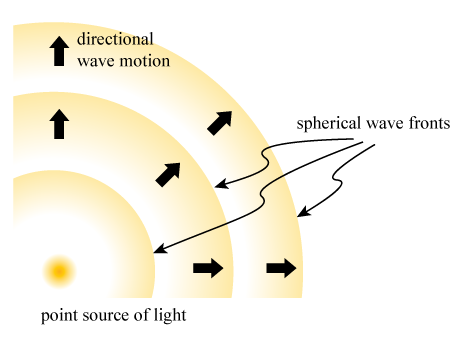

A point source of light is at the lower left corner emitting spherical wave fronts in all directions. In the figure, segments of three spherical surfaces at different radii are shown and are labeled spherical wave fronts. There are several arrows in the middle and outer radii pointing radially outward and are labeled directional wave motion.

Figure 1

In our investigation of the optical systems in this lab, it is helpful to define another way of describing these wave disturbances and their propagation through the optical medium. We want to introduce the concept of a ray to describe the direction of propagation of these light waves in the medium. A ray is an imaginary line along the direction of propagation of the wave that is perpendicular to the wave front of this disturbance. When waves travel through an isotropic and homogenous medium, these rays will be straight lines. We will use these rays to study in more detail what happens when a light disturbance encounters mirrors and boundaries between different optical media as it propagates through space.

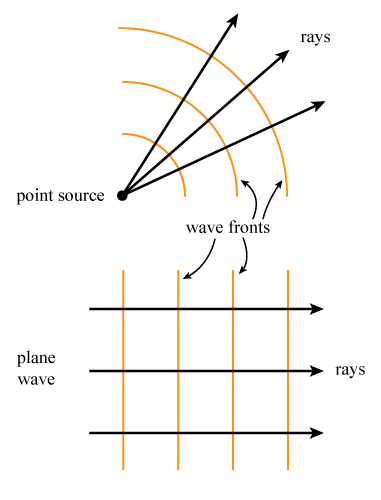
There are two images in the figure. The top image has a point source and three circular arcs which are at equal intervals from the point source. These circular concentric arcs centered on the point source are labeled wave fronts and are only drawn in the first quadrant (from 0 to 90 degrees counterclockwise). Three arrows labeled rays are radially pointing out from the point source at angles of about 25 degrees, 45 degrees and 60 degrees. The bottom image at the bottom has four vertical lines and three horizontal arrows pointing to the right at equal intervals. The horizontal arrows are labeled rays. On the leftmost side, there is a label plane wave. The vertical lines are labeled wave fronts.

Figure 2

Index of Refraction

We can define a quantity called the index of refraction, n, of an optical media as the ratio of the speed of light in vacuum divided by the speed of light in the medium. Since nothing can go faster than the speed of light, including light, this ratio is always greater than or equal to 1.

( 1 )

n =

v_medium

(index of refraction)

Light that has entered a material from vacuum will slow down in that material and we describe this light as having been refracted by this medium.

The Laws of Reflection and Refraction

If we now investigate what happens to light that is incident on a surface between to different optical media, we find the following laws apply.

1
The incident, reflected, refracted rays and the normal to the surface all lie in the same plane.
2
The angle of reflection as measured with respect to the normal to the surface is always equal to the angle of incidence, also measured with respect to the normal to the surface. This is true for all wavelengths of light and for any pair of materials that you may choose.

( 2 )

θ_r = θ_a (law of reflection)

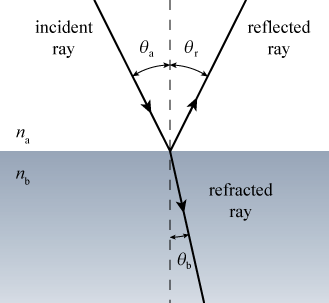
$There are two mediums in the image. Medium n_a is at the top half and medium n_b is at the lower half. An incident ray represented by an arrow is traveling through medium n_a and is incident at some angle on the second medium n_b. There is a vertical dashed line where the incident ray meets the second medium. All the angles are measured from this vertical line. The angle between the incident ray and the vertical line is labeled theta_a. The reflected ray represented by another arrow, points up in medium n_a at angle theta_r from the vertical line. Thus, the angle theta_a and theta_r are on either side of the vertical line. At the point where the incident ray meets the medium n_b, a refracted ray represented by an arrow travels down the medium n_b at an angle theta_b from the vertical line.$

Figure 3

3
For light of a single wavelength incident on this surface, we find that the ratio of the sines of the incident ray as measured to the normal divided by the refracted ray is equal to the inverse of the ratio of the indices of refraction for these two materials.

( 3 )

n_a sin θ_a = n_b sin θ_b (Snell's Law)

Objective

In this lab, you will use these basic principles of reflection and refraction to study several different simple optical systems. In each of these exercises, you will use a source of parallel light rays to study how they behave in these different configurations. The goal of this lab is to have you verify the above relationships.

Apparatus

Multi-ray light source
Mounted mirror
Concave/convex mirror
Double-concave lens
Masking tape
Double-convex lens
Plano-convex lens
Prism
Protractor

Figure 4

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Reflection from a Plane Surface

Set up the multi-ray light source to produce only one light ray. You may have to use masking tape to cover the extra slits. Set the small plane mirror in a vertical position in front of the light source on a sheet of paper. Position the face of the mirror perpendicular to the light ray and mark the position of the mirror and the path of the light ray on the paper.

The angle between the incident light ray (the light ray that shines on the mirror directly from the light source) and a line normal to the mirror is called the angle of incidence. The angle between the reflected light ray and the line normal to the mirror is called the angle of reflection. When the mirror is perpendicular to the incident light ray, the reflected light ray is directly along the path of the incident ray and thus the incident angle and the reflected angle are both equal to zero.

Rotate the plane mirror such that the incident angle is approximately 30° from the normal. Trace the incident and reflective lines on a sheet of paper and measure the angle of reflection with a protractor. Repeat this procedure with incident angles of 45° and 60°. See Figure 5.

A single light ray originating from a light source is incident on a plane mirror at some angle from the normal. This apparatus sits on top of a piece of paper and an arrow drawn on the paper indicates the incident and reflected rays.

Figure 5

Remove the masking tape (if used) from the other slits on the light source and shine the light rays on the plane mirror. Trace the light rays and try to determine if the mirror image of an object is reversed. Explain your steps.

Concave and Convex Mirrors and Lenses

Reflection from a Concave Mirror

For this experiment, you will need three or more parallel light rays. The plano-convex lens (used to collimate the light rays) should now be placed in front of the slits of the multi-ray light source.

Place the concave mirror such that the light rays reflect back toward the light source and that the principal focus f of the mirror converges along the central ray (see Figure 6).

There are three objects in this figure. A plano-convex lens is placed in front of the light source to produce some parallel light rays. These parallel rays are incident on a concave mirror such that the light rays are reflected back and converge at a point in front of the concave mirror.

Figure 6

Trace the light rays on a sheet of paper (be sure to mark the location of the mirror).

Find the focal length of the mirror.

Reflection from a Convex Mirror

Turn the concave mirror around and use it as a convex mirror (see Figure 7).

Trace the light rays and find the focal length of the convex mirror. Again, be sure to mark the location of the mirror. Note that the focal point of this convex mirror cannot be observed directly. You may only determine this from the ray diagram.

Figure 7

Refraction by a Convex Lens

Position the convex lens as shown in Figure 8.

Figure 8

Find the focal length of the lens.

Refraction by a Concave Lens

Position the concave lens as shown in Figure 9.

Find the focal length of the lens by tracing the lines on a sheet of paper. Note that you must trace the diverging refracted light rays back to the focal point of the lens.

Figure 9

More Experiments with Concave–Convex Lenses

Position the lenses different distances and in different order from the light source and observe the various ray diagrams that are produced. An example is shown in Figure 10. Try others.

There are four objects in this figure. A plano-convex lens is placed in front of the light source to produce some parallel light rays. A convex lens and then a concave lens are placed in front of these light rays.

Figure 10

Reflection/Refraction by Prism

Angle of the Prism

Position the prism as shown in Figure 11. Adjust the light source such that two parallel rays are produced.

$There are three objects in this figure. A plano-convex lens is placed in front of the light source to produce two parallel light rays. A prism is placed in the path of the light rays such that one of the vertices of the triangle is facing the light source and the two parallel light rays are incident on the two sides of the prism. These rays produce refracted and reflected rays. The angle between the two reflected rays from the two sides of the prism is labeled R.$

Figure 11

You will now measure the angle, R, of the prism.

a
When the prism is positioned in the path of the light rays, a refracted ray and a reflected ray are produced.

b
The reflected ray will be used to find the angle, R.

c
Note that the angle between the two reflected rays is equal to 2R. Why?

d
Determine R.

How does your measurement compare to a direct measurement of the angle of the prism?

Index of Refraction of the Prism

Adjust the light source so that only one light ray is produced. Position the light source and the prism as shown in Figure 12.

From your measurement of the angle of deviation, D, find the index of refraction of the prism.

$There are three objects in this figure. A plano-convex lens is placed in front of the light source to produce a single light ray. This light ray is incident on one side of the prism at some angle from the normal. The refracted ray is seen coming out of the other side of the prism. There is also a line that traces the original incident ray.$

Figure 12

Total Internal Reflection

We will now investigate how the light is reflected and refracted if it is incident on the boundary between two materials from the side with the larger index of refraction. Take your light source and prism from the last setup and arrange the prism so that the light ray enters the prism and is aimed in order that it exits the prism on its longest side.

First arrange the light beam so that it is normally incident on this surface from inside the prism. What is the angle of refraction of the light as it leaves the prism?

Now begin to gradually rotate the prism in order that the angle of incidence inside the prism increases.

Pick an angle here and measure both the incident angle in the prism and the refracted angle in air and see if these angles are consistent with your earlier measurement of the index of refraction of the prism.

As you continue to gradually increase the angle of incidence for the light ray inside the prism, you should find an angle where there is NO refracted ray of light that leaves the prism. What is the value of this angle?

Is this consistent with Snell's Law and the value of the index of refraction that you measured earlier?

The angle where the rays are not able to exit the higher index material is called the critical angle. How does this angle depend on the indices of refraction of the two materials?