Lab 5 - Impulse, Momentum, and Energy

Introduction

Newton expressed what we now call his second law of motion, not as

= ma

but in terms of the rate of change of momentum of the object

/dt.

In this more general and powerful form the law states that when an unbalanced force acts on a body during a finite but short time interval, the change in the object's momentum depends on the product of the force and the time interval for which the force acts. The quantity

is defined as Impulse and the relationship between the change in momentum and the Impulse is sometimes referred to as the Impulse-Momentum Theorem. It states that the integral of the force with respect to time is equal to the change in momentum of the object.

Discussion of Principles

Impulse-Momementum Theorem

When an unbalanced force

_net

acts on an object for a time interval

Δt,

the momentum of the object will change over this time interval. If

and

are the initial and final momenta at the start and end of this time interval respectively, then Newton's second law can be written as

( 1 )

_net Δt = Δp

The product

_net Δt,

when summed over several small time intervals, is the integral of

_net dt

and is defined as the Impulse

( 2 )

t_f	F_netdt

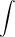t_i

= p

_f − p

Note that impulse is a vector quantity and has the same direction as the change in momentum vector. Figure 1 is a graph of the net force versus time. When the force is constant over a time interval, then the integral of

_net

over the time interval is the area of the rectangle under the force line and bounded by the two time values. This is shown by the shaded region in Fig. 1a. The example in Fig. 1b is for a non-uniform force acting over an interval of time. In this case, the impulse would again be the area under the force-time curve as indicated by the shaded region.

Figure 1: Impulse as area under force-time curve

Work-Energy Theorem

The simplest form of the Work-Energy Theorem states that the change in kinetic energy of an object is equal to the total work done on that object.

( 3 )

ΔK = W

The work done can be divided into

W_C,

the work done by conservative forces like gravity, and

W_NC,

the work done by non-conservative forces like friction, so that Eq. (3) can be written as

( 4 )

ΔK = W_C + W_NC

Since

W_C = −ΔU,

where

ΔU

is the change in the potential energy of the object, this can be rewritten as

( 5 )

ΔK + ΔU = W_NC

( 6 )

W_NC	=	(K_f − K_i) + (U_f − U_i)
	=	(K_f + U_f) − (K_i + U_i)
	=	(E_f − E_i)

where

E_i

is the initial value of the total mechanical energy of the object and

E_f

is the final value of the total mechanical energy of the object. Therefore,

( 7 )

W_NC = ΔE

Equation (7) states that the total change in the mechanical energy of an object is equal to the work done by non-conservative forces.

Objective

In this lab, you will verify the impulse-momentum theorem by investigating the collision of a moving cart with a fixed spring. You will also use the work-energy theorem to evaluate the energy losses during the collision.

Equipment

Track
Force sensor with spring bumper
Cart with low friction wheels
Photogate
Meter stick

Procedure

The experimental setup consists of a long, inclined track to which a force sensor with a spring is attached. See Fig. 2. A cart will be released from the high side of the track and will roll down the incline, collide with the spring, and then roll back up the incline. A photogate will be placed just in front of the spring to measure the speed of the cart just before and just after the collision.

Figure 2: A force sensor with spring bumper

The cart moves down the track, collides with the spring, and goes back up the track. The force sensor will record the force of this collision at equally spaced time intervals. Plotting this force information, you will be able to determine impulse from the area under the force vs. time curve. From the initial and final speeds of the cart recorded by the photogate measurements you can determine the change in momentum of the cart. You can then compare the impulse to the change in momentum to validate the impulse-momentum theorem. During this process, some of the cart's energy will be lost due to the action of non-conservative forces. You will be able to see this in two ways. First, the initial and final speeds recorded by the photogate will not be equal, indicating that energy is lost due to the action of non-conservative forces during the collision. According to Eq. (7), the energy lost during the collision is equal to the work done by these non-conservative forces.

( 8 )

ΔE_collision = W_NC^collision

Secondly, after the collision, the cart will return to a point on the inclined track that is lower than the point from which it was initially released. This shows a net loss of energy over the entire trip. Some of this energy is lost during the collision as shown in Eq. (8), and some is lost to other non-conservative forces acting while the cart travels down and up the ramp. Therefore, the total energy lost during the entire trip will be equal to the work

W_NC^collision

done by non-conservative forces during the collision, plus the work

W_NC^traveling

done by the other non-conservative forces acting while the cart travels along the track. In other words,

( 9 )

ΔE_total = W_NC^collision + W_NC^traveling

Let's now try to determine these energy losses in terms of quantities that can be determined experimentally. We will first focus on the energy loss that occurs over the entire trip,

ΔE_total.

Figure 3 is a diagram of the trip taken by the cart.

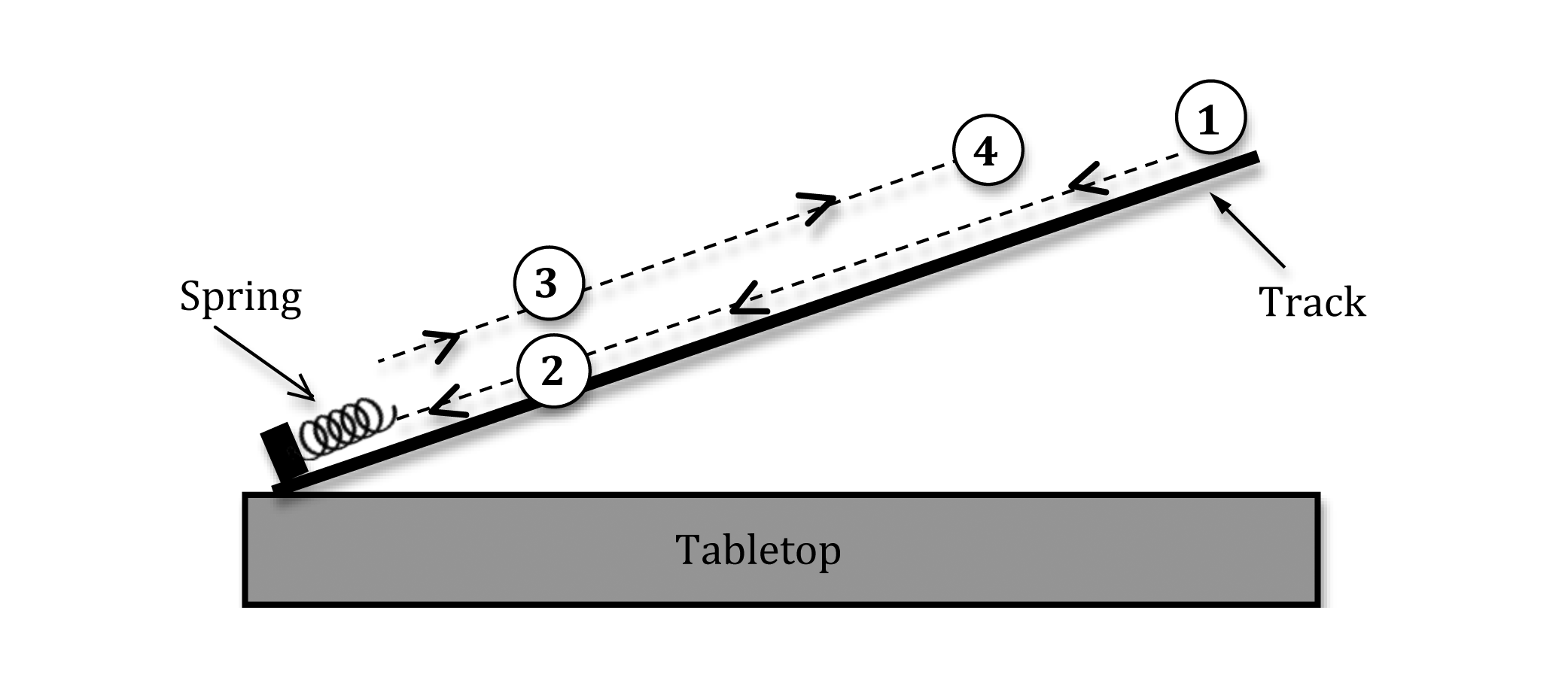
Figure 3: Diagram of the path of the cart

The cart is released from location Point one

, travels down the ramp and first passes through the photogate at location Point two

just before the collision. This is represented by the thin dashed line with arrows pointing down the track. The cart then bounces off the spring and passes back through the photogate at location Point three

just after the collision. This is represented by the thin dashed line with arrows pointing up the track. Note that locations Point two

and

are actually the same positions on the track. Finally, the cart returns to location Point four

, which is lower on the track than the initial starting location Point one

. The two dashed lines are displaced from each other for clarity. Combining Eqs. (5) and (7) we get

( 10 )

ΔE_total = ΔK_total + ΔU_total

where

ΔK_total = K₄ − K₁

and

ΔU_total = U₄ − U₁.

Since the cart is released from rest and returns to rest,

K₄ = K₁ = 0

and

( 11 )

ΔE_total = U₄ − U₁.

If we focus on determining the energy loss just in the collision itself (i.e., from location Point two

on the way down back to location Point three

on the way up), we have

( 12 )

ΔE_collision = ΔK_collision + ΔU_collision

where

ΔK_collision = K₃ − K₂

and

ΔU_collision = U₃ − U₂.

Since the cart is at the same height each time it passes through the photogate

U₃ = U₂

and we get

( 13 )

ΔE_collision = K₃ − K₂.

Equations (11) and (13) can be used to determine the total energy loss and the energy loss just in the collision, respectively. Then, this information can be combined with Eqs. (4) and (5) to determine the work,

W_NC^collision,

done by non-conservative forces during the collision, and the work,

W_NC^traveling,

done by other non-conservative forces while the cart travels along the track.

Initial set-up

The equipment consists of a straight track, a cart with low friction wheels, a force sensor with a spring bumper, and a photogate. A computer acquires, stores, and displays the data collected by the photogate and force sensor.

Weigh and record the mass of the cart on the worksheet.

Measure the width of the flag on the cart and record it on the worksheet.

Make sure the track is set up so that the yellow, ruled strip is facing you, and make the side of the track flush with the edge of the table.

Elevate the starting end of the track about 4 to 5 centimeters so that the cart can roll toward the spring bumper.

Move the track so that the end with the force sensor is firmly against the stop.

Set the photogate so that the flag clears it 1 to 2 centimeters before the cart hits the spring bumper.

Calibrating the Force Sensor

Open the appropriate DataStudio file associated with this lab. The force probe will automatically be routed to analog channel A and the photogate will automatically be routed to digital channel 1.

Click the Experiment Setup window. See Fig. 4.

Click the Constants tab and input your flag width.

Figure 4: DataStudio window showing input for flag width

Click the FORCE SENSOR in the middle of the window.

Then click the Calibrate Sensors button at the top of the Experiment Setup window. See Fig. 5.

Figure 5: Calibrate sensors

Remove the force sensor from the track by loosening the bolts on the side.

After the Calibrate Sensors window opens go through the following steps. Hang the 500 g (4.95 N) mass from the spring (the force sensor should be in one hand with the mass hanging below the sensor). Click Read From Sensor and input –4.9 N in the Calibration Point 1 box. Notice the (–) sign. Remove the mass. Flip the sensor so that the spring is pointing up toward the ceiling. Steady the 500 g (4.95 N) mass on the spring. Click Read From Sensor and input +4.9 N in the Calibration Point 2 box. Notice the (+) sign. Click OK to complete the calibration process.

Return the force sensor to the track and tighten. Make sure the force sensor, clamp, and track all remain in place when car slides down the track and hits them. Now you are ready to begin the lab!

Data Acquisition

Select a starting point about 60 cm from the end of the spring bumper. Record this on the worksheet as the starting position. Note: This is the distance up the ramp from the uncompressed spring.

Use the meter stick to measure the vertical distance from the bottom of the tabletop to the top edge of the track at the starting position. Record this in the worksheet as the starting position height.

Place the cart so that the end with the flag is towards the spring bumper and the front end is lined up with the starting position.

Click the START button to start the data acquisition program and then release the cart, being careful not to push it either up or down the track. The cart should go through the photogate once on its way down and once on its way up the track for a total of two passes. Now click the STOP button. Practice steps 17 and 18 a few times before performing the experiment. You should be able to get the cart to return to roughly the same place each time it is released, and you should have a nice, smooth force vs. time curve like the one shown in Fig. 6.

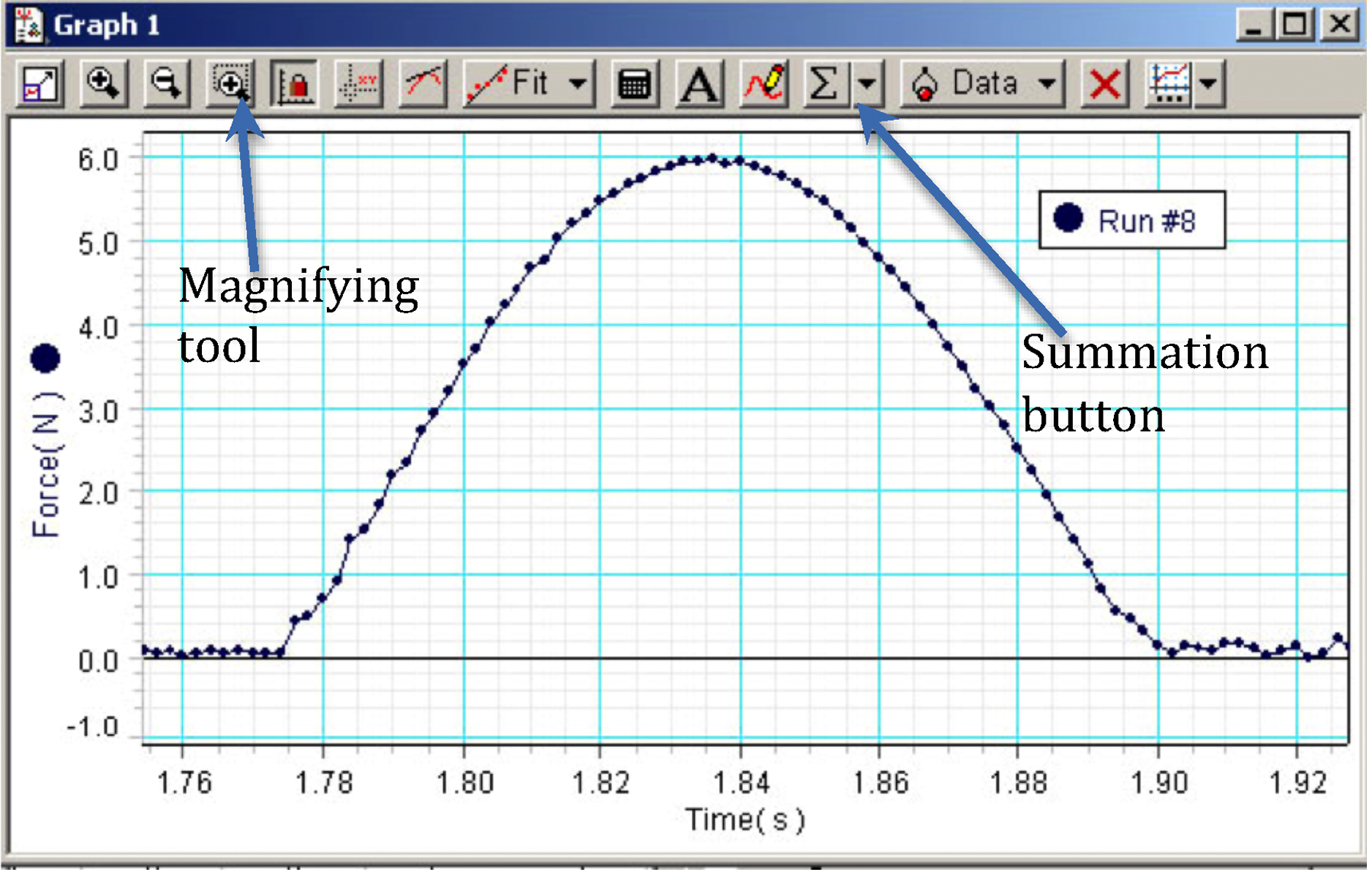
Figure 6: Screenshot showing plot of spring force versus time

Observe the position of the back end of the cart (the end that was originally at the starting position) when it temporarily stops at its maximum height. Record this on the worksheet as the stopping position.

Measure the vertical distance from the bottom of the tabletop to the top edge of the track at the stopping position. Record this in Data Table 1 in the worksheet.

Record the values of the initial and final speeds of the cart in Data Table 1. Do not delete the data set. You will need it for future analysis.

Checkpoint 1:
Ask your TA to check your data from the first run before proceeding.

Repeat this procedure two more times with the exact same starting position.

Record the stopping position, track height, and the initial and final cart speeds each time in Data Table 1. At the end of this procedure, you should have three nice graphs of force vs. time, three sets of initial and final cart speeds, and three sets of stopping positions and track heights.

Checkpoint 2:
Ask your TA to check your data from the last 2 runs before proceeding.

Procedure A: Impulse

For each of the trials do the following. In the DataStudio window, click the magnifying tool (see Fig. 6) with the dotted line around it in the top left. Use this repeatedly to zoom in on just the portion of the graph where your cart hit the spring. With just this portion of your graph highlighted, click the summation button at the top mid-right of the DataStudio window, and from the menu select Area. This will automatically calculate the area under the highlighted portion of your graph. Enter this value of the area in Data Table 2 in the worksheet. For one of the graphs calculate the area by the trapezoid method to compare with the value obtained from the computer software. Construct rectangles between 2 data points with a height equal to the average of the 2 data points. Then the area is the sum of the areas of these rectangles.

Use the photogate speeds to compute the magnitude of the change in momentum of the cart for each trial and record these in Data Table 2 in the worksheet.

Calculate and record the average values of the area and change in momentum.

Compare the average area with the average change in momentum by computing the percent difference. See Appendix B.

Checkpoint 3:
Ask your TA to check your impulse calculations.

For each trial, use the initial and final speeds recorded by the photogate to calculate the energy loss during the collision. Record these in Data Table 3 on the worksheet.

For each trial, use the starting height and stopping height to compute the total energy loss for the entire trip. Record these values in Data Table 3.

Compute and record the average values of

ΔE_collision

and

ΔE_total.

Use these average values to determine the percentage of the total energy loss that occurred during the collision.

Use the average energy losses to determine the amount of work done by non-conservative forces during the collision as well as the amount of work done by other non-conservative forces during the rest of the cart's trip.

Checkpoint 4:
Ask your TA to check your energy loss calculations.