Record-Keeping and Calculations

Forms

Miscellaneous Useful Calculations

Few experiments will involve very complicated calculations. However, most will require several relatively simple computations. You must be able to do these computations rapidly and accurately. Review your General Chemistry material if any of the following calculations appear to be difficult or new to you.

Mass Volume

Very often it will be more convenient to measure reagents by volume. This saves the time of weighing. If the density is known, the volume can be simply converted to mass so that the number of moles may be calculated. The density can be obtained from the container label, a chemical catalog, the MSDS, or from one of the tables in the "Handbook of Chemistry and Physics."

( 1 )

Density =

Mass

Volume

The density ( "d") of water is 1 g/cc. The density of acetone is 0.791 g/cc. Thus, one cc of acetone weighs 0.791 g.

Question: What volume must we use if we need 16 g of acetone?

Mass

Density

Volume

16 g

0.791 g/cc

20 cc since we had only two significant figures in the weight (16 g)

Question: What mass of acetone is contained in 75.2 mL? (1 cc = 1 mL)

Volume × Density	=	Mass

75.2 mL × 0.791 g/mL	=	59.5 g NOTE three significant figures in this case

Gram Formula Weight

We will be using molecular formulas throughout this course. You should be able to determine the gram formula weight (or molecular weight) given the molecular formula of a compound.

Question: What is the gram formula weight of acetone (C₃H₆O)?

3 Carbons	= 3 ×	12.011	=	36.033
6 Hydrogens	= 6 ×	1.0079	=	6.0474
1 Oxygen	= 1 ×	15.9994	=	15.9994
				58.0798

or, 58.08 g/g formula weight = 58.08 g/mole (Molecular Weights (Gram Formula Weights) are generally reported to only two decimal places.)

Question: What is the gram formula weight of sodium dichromate? When we look up sodium dichromate in a handbook or catalog, we find that it is usually found as the dihydrate

(Na₂Cr₂O₇ · 2 H₂O).

2 Sodiums	= 2 ×	22.9898	=	45.9796
2 Chromiums	= 2 ×	51.996	=	103.992
9 Oxygens	= 9 ×	15.9994	=	143.9946
4 Hydrogens	= 4 ×	1.0079	=	4.0316
				297.9978

or, 298.0 g/g formula weight = 298.0 g/mole

Question: What is the percent chromium in this salt?

Mass of Chromium

Mass of the Salt

× 100

Percent Chromium

103.9

298.0

× 100

34.87% Cr in Na₂Cr₂O₇ · 2 H₂O

Moles/Mass

One of the most useful applications of the gram formula weight is the determination of the number of moles of a substance.

Question: How many moles of sodium dichromate dihydrate (Na₂Cr₂O₇ · 2 H₂O) are present in 26.5 g of that material?

1 mole = 298.0 g therefore,

26.5 g

298.0 g/mole

= 0.0889 moles

Question: How many grams of acetone must I use if I want 3.6 moles?

Moles × g Formula Weight	=	Mass
3.6 moles × 58.08 g/mole	=	210 g

Question: What is the volume of this much acetone?

Mass

Density

Volume

210 g

0.791 g/cc

265 cc = 265 mL

Percent Yield

Before trying to calculate a percent yield, it is necessary to have a balanced equation. For the allylic substitution reaction of bromine (Br₂) with cyclohexene (C₆H₁₀), the equation is illustrated in the figure below.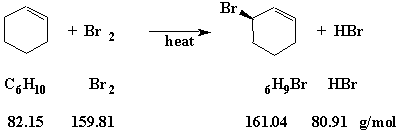

Figure 1

Question: In one experiment, we used 20.1 g of cyclohexene and 20.5 g of bromine. Which reagent is the "Limiting Reagent;" what is the "Theoretical Yield" of the product (3-bromocyclohexene); and what is the "Percent Yield" if the reaction produced 5.2 g of product? To determine the "Limiting Reagent" we first look at the balanced equation. That equation tells us that it takes one mole of bromine to react completely with one mole of cyclohexene. We must next calculate how many moles we have of each of the reagents.

Moles of Cyclohexene

20.1 g

82.15 g/mole

0.245 moles

Moles of Bromine

20.5 g

159.82 g/mole

0.128 moles

Since we have about twice as many moles of cyclohexene as bromine, we will run out of bromine first. Therefore, bromine is the "Limiting Reagent." Since we have only 0.128 moles of the "Limiting Reagent" (bromine), the maximum quantity of product that could be produced is only 0.128 moles. The "Theoretical Yield" of 3-bromocyclohexene is therefore 0.128 moles × 161.04 g/mole = 20.6 g (Significant Figures). The maximum amount of product that could be produced is 20.6 g.

Question: But what is the "Percent Yield" if the reaction actually produced 5.2 g of product?

Actual Yield

Theoretical Yield

× 1000

Percent Yield

5.2 g/20.6 g × 100

25%

Each time you run a reaction starting with known quantities of material, you should determine the "Limiting Reagent," "Theoretical Yield," and "Percent Yield." Be sure to use a correctly balanced equation and the correct gram formula weights. Double-check all calculations. It is very easy to skip a decimal point or misread a figure on a calculator.