Lab 7 - Simple Harmonic Motion
Introduction
Have you ever wondered why a grandfather clock keeps accurate time? The motion of the pendulum is a particular kind of repetitive or periodic motion called simple harmonic motion, or SHM. The position of the oscillating object varies sinusoidally with time. Many objects oscillate back and forth. The motion of a child on a swing can be approximated to be sinusoidal and can therefore be considered as simple harmonic motion. Some complicated motions like turbulent water waves are not considered simple harmonic motion. When an object is in simple harmonic motion, the rate at which it oscillates back and forth as well as its position with respect to time can be easily determined. In this lab, you will analyze a simple pendulum and a spring-mass system, both of which exhibit simple harmonic motion.Discussion of Principles
A particle that vibrates vertically in simple harmonic motion moves up and down between two extremes y = ±A. The maximum displacement A is called the amplitude. This motion is shown graphically in the position-versus-time plot in Fig. 1.
Figure 1: Position plot showing sinusoidal motion of an object in SHM
y = −A
to y = +A
and back again to y = −A.
The time interval T required to complete one oscillation is called the period. A related quantity is the frequency f, which is the number of vibrations the system makes per unit of time. The frequency is the reciprocal of the period and is measured in units of Hertz, abbreviated Hz; 1 Hz = 1 s−1.
( 1 )
f = 1/T
( 2 )
y = A sin(2πft)
( 3 )
v = 2πfA cos(2πft)
( 4 )
a = −(2πf)2[A sin(2πft)]
f = 1/T
into Eq. (4) a = −(2πf)2[A sin(2πft)]
yields
( 5 )
a = −4π2f2y
a = −4π2f2y
we see that the acceleration of an object in SHM is proportional to the displacement and opposite in sign. This is a basic property of any object undergoing simple harmonic motion.
Consider several critical points in a cycle as in the case of a spring-mass system in oscillation. A spring-mass system consists of a mass attached to the end of a spring that is suspended from a stand. The mass is pulled down by a small amount and released to make the spring and mass oscillate in the vertical plane. Figure 2 shows five critical points as the mass on a spring goes through a complete cycle. The equilibrium position for a spring-mass system is the position of the mass when the spring is neither stretched nor compressed.
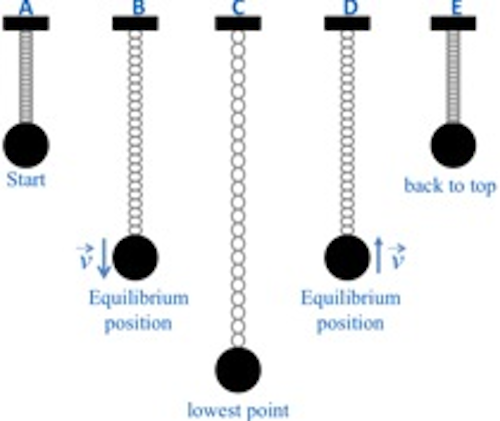
Figure 2: Five key points of a mass oscillating on a spring.
-
Position A: The spring is compressed; the mass is above the equilibrium point at y = Aand is about to be released.
- Position B: The mass is in downward motion as it passes through the equilibrium point.
- Position C: The mass is momentarily at rest at the lowest point before starting on its upward motion.
- Position D: The mass is in upward motion as it passes through the equilibrium point.
- Position E: The mass is momentarily at rest at the highest point before starting back down again.
| Position | Velocity | Acceleration | |
| Point A | neg max | zero | pos max |
| Point B | zero | pos max | zero |
| Point C | pos max | zero | neg max |
| Point D | zero | neg max | zero |
| Point E | neg max | zero | pos max |
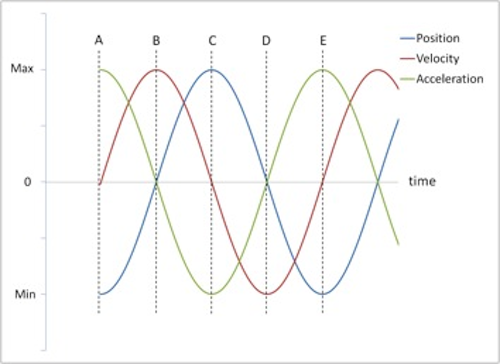
Figure 3: Position, velocity and acceleration vs. time
Mass and Spring
A mass suspended at the end of a spring will stretch the spring by some distance y. The force with which the spring pulls upward on the mass is given by Hooke's law( 6 )
F = −ky
Δy
. This experimental set-up is also shown in the photograph of the apparatus in Fig. 5.

Figure 4: Set up for determining spring constant

Figure 5: Photo of set-up for determining spring constant
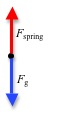
Figure 6: Free-body diagram for the spring-mass system
( 7 )
Δmg − kΔy = 0
Δm
is the change in mass and Δy
is the change in the stretch of the spring caused by the change in mass, g is the gravitational acceleration, and k is the spring constant. Eq. (7) Δmg − kΔy = 0
can also be expressed as
( 8 )
Δm =
Δy
| k |
| g |
ma = F = −ky.
Substitute from Eq. (5) a = −4π2f2y
for the acceleration to get
( 9 )
m(−4π2f2y) = −ky
( 10 )
f =
| 1 |
| 2π |
 |
|
( 11 )
T = 2π
 |
|
T = 2π
we can predict the period if we know the mass on the spring and the spring constant. Alternately, knowing the mass on the spring and experimentally measuring the period, we can determine the spring constant of the spring.
Notice that in Eq. (11)  |
|
T = 2π
the relationship between T and m is not linear. A graph of the period versus the mass will not be a straight line. If we square both sides of Eq. (11) |
|
T = 2π
, we get
 |
|
( 12 )
T2 = 4π2
| m |
| k |
T2
versus m will be a straight line and the spring constant can be determined from the slope.
Simple Pendulum
The other example of simple harmonic motion that you will investigate is the simple pendulum. The simple pendulum consists of a mass m, called the pendulum bob, attached to the end of a string. The length L of the simple pendulum is measured from the point of suspension of the string to the center of the bob as shown in Fig. 7 below.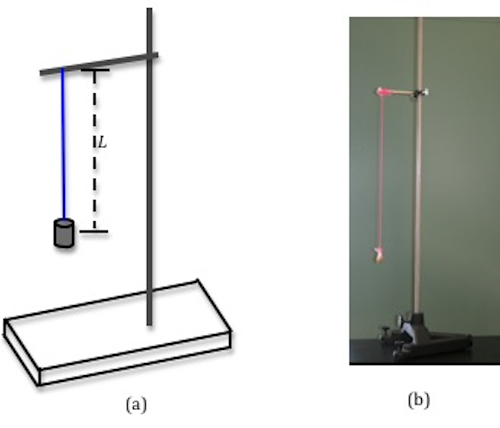
Figure 7: Experimental set-up for a simple pendulum
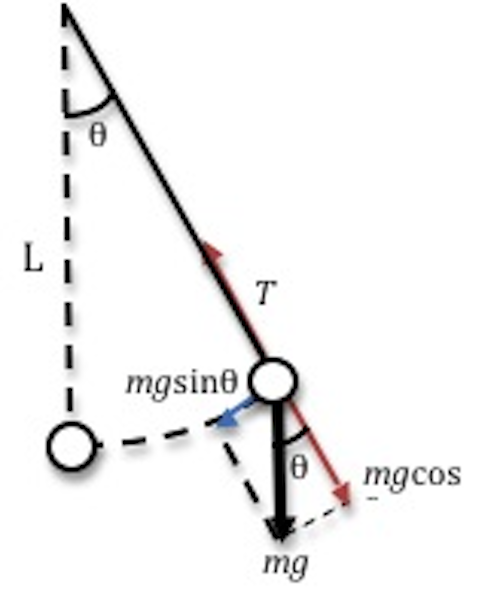
Figure 8: Simple pendulum
|F | = mg sin θ.
| = mg sin θ.
This force depends on the mass of the bob, the acceleration due to gravity g and the sine of the angle through which the string has been pulled. Again Newton's second law must apply, so
 | = mg sin θ.
| = mg sin θ.( 13 )
ma = F = −mg sin θ
α = a/L.
From Eq. (13) ma = F = −mg sin θ
we get
( 14 )
α = −
sin θ
| g |
| L |
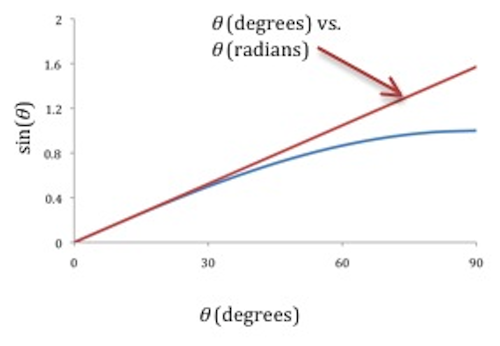
Figure 9: Graphs of sin θ versus θ
α = −
sin θ
becomes
| g |
| L |
( 15 )
α = −
θ
| g |
| L |
a = −4π2f2y
to get
( 16 )
α = −4π2f2 θ
α = −
θ
and Eq. (16)| g |
| L |
α = −4π2f2 θ
, and simplifying, we get
( 17 )
f =
| 1 |
| 2π |
 |
|
( 18 )
T = 2π
 |
|
Objective
The objective of this lab is to understand the behavior of objects in simple harmonic motion by determining the spring constant of a spring-mass system and a simple pendulum.Equipment
- Assorted masses
- Spring
- Meter stick
- Stand
- Stopwatch
- String
- Pendulum bob
- Protractor
- Balance
Procedure
Using Hooke's law you will determine the spring constant of the spring by measuring the spring stretch as additional masses are added to the spring. You will determine the period of oscillation of the spring-mass system for different masses and use this to determine the spring constant. You will then compare the spring constant values obtained by the two methods. In the case of the simple pendulum, you will measure the period of oscillation for varying lengths of the pendulum string and compare these values to the predicted values of the period.Procedure A: Determining Spring Constant Using Hooke's Law
-
1Starting with 50 g, add masses in steps of 50 g to the hanger. As you add each 50 g mass, measure the corresponding elongation y of the spring produced by the weight of these added masses. Enter these values in Data Table 1.
-
2Use Excel to plot m versus y. See Appendix G.
-
3Use the trendline option in Excel to determine the slope of the graph. Record this value on the worksheet. See Appendix H.
-
4Use the value of the slope to determine the spring constant k of the spring. Record this value on the worksheet.
Checkpoint 1:
Ask your TA to check your table and Excel graph.
Ask your TA to check your table and Excel graph.
Procedure B: Determining Spring Constant from T2 vs. m Graph
We have assumed the spring to be massless, but it has some mass, which will affect the period of oscillation. Theory predicts and experience verifies that if one-third the mass of the spring were added to the mass m in Eq. (11)T = 2π
, the period will be the same as that of a mass of this total magnitude, oscillating on a massless spring.
 |
|
-
5Use the balance to measure the mass of the spring and record this on the worksheet. Add one-third this mass to the oscillating mass before calculating the period of oscillation. If the mass of the spring is much smaller than the oscillating mass, you do not have to add one-third the mass of the spring.
-
6Add 200 g to the hanger.
-
7Pull the mass down a short distance and let go to produce a steady up and down motion without side-sway or twist. As the mass moves downward past the equilibrium point, start the clock and count "zero." Then count every time the mass moves downward past the equilibrium point, and on the 50th passage stop the clock.
-
8Repeat step 7 two more times and record the values for the three trials in Data Table 2 and determine an average time for 50 oscillations.
-
9Determine the period from this average value and record this on the worksheet.
-
10Repeat steps 7 through 9 for three other significantly different masses.
-
11Use Excel to plot a graph ofT2vs.m.
-
12Use the trendline option in Excel to determine the slope and record this value on the worksheet.
-
13Determine the spring constant k from the slope and record this value on the worksheet.
-
14Calculate the percent difference between this value of k and the value obtained in procedure A using Hooke's law. See Appendix B.
Checkpoint 2:
Ask your TA to check your table values and calculations.
Ask your TA to check your table values and calculations.
Procedure C: Simple Pendulum
-
15Adjust the pendulum to the greatest length possible and firmly fasten the cord. With a 2-meter stick, carefully measure the length of the string, including the length of the pendulum bob. Use a vernier caliper to measure the length of the pendulum bob. See Appendix D. Subtract one-half of this value from the length previously measured to get the value of L and record this in Data Table 3 on the worksheet.
-
16Using the accepted value of 9.81m/s2for g, predict and record the period of the pendulum for this value of L.
-
17Pull the pendulum bob to one side and release it. Use as small an angle as possible, less than 10°. Make sure the bob swings back and forth instead of moving in a circle. Using the stopwatch measure the time required for 50 oscillations of the pendulum and record this in Data Table 3.
-
18Repeat step 17 two more times and record the values for the three trials in Data Table 3 and determine an average time for 50 oscillations.
-
19Determine the period from this average value and record this on the worksheet.
-
20Calculate the percent error between this value and the predicted value of the period.
-
21Repeat steps 16 through 20 for three other significantly different lengths.
Checkpoint 3:
Ask your TA to check your table values and calculations.
Ask your TA to check your table values and calculations.

