Lab 3 - DC Circuits and Ohm's Law

Introduction

During the nineteenth century so many advances were made in understanding the electrical nature of matter that it has been called the "age of electricity." One such advance was made by a German physicist named Georg Simon Ohm. Ohm was interested in examining the relative conductivity of metals and in investigating the relationship between the electromotive force (potential difference) and the current in a conductor. By taking wires made from different materials but having the same thickness, passing a current through these wires, and measuring the electromotive force, i.e., the potential difference between the ends of the conducting wire, he was able to determine experimentally the relative conductivity of certain metals such as silver, copper, and gold. In another experiment using a piece of apparatus that he built, Ohm investigated the effect of current in a conductor on the voltage drop across the conductor. He found that for a given conductor the voltage drop was directly proportional to the current in the wire. When voltage is plotted against the current in a given conductor, the data can be fitted to a straight line, the slope of which is the resistance of the conductor. This result was published in 1826. In recognition of Ohm's work, this empirical relationship bears his name.

Discussion of Principles

Ohm's Law can be written algebraically as ΔV = RI, where ΔV, measured in volts, represents the potential drop or potential difference across the conductor, I is the current in the conductor measured in amperes, and R is the resistance of the conductor measured in units called "ohms" symbolized by Ω, upper-case Greek omega. Note: Some textbooks use V rather than ΔV for potential difference.

Resistance and Resistors

Resistance is a property of materials. Resistors are conducting devices made from materials, which satisfy Ohm's Law. If the potential difference across a resistor is set at 1 volt, and if a current of 1 amp is measured in the conductor, then its resistance is determined to be 1 ohm, or 1 Ω. Instead of using thin wires as Ohm did in his original experiment, you will replicate his results using small cylindrical ceramic resistors.

Figure 1: Color-coded ceramic resistors

You will notice colored bands on the resistors. These bands form a code that indicates the resistance of the resistor. Later we will discuss how to read this color code.

Combinations of Resistors

Resistors can be combined in simple circuit arrangements that increase or decrease the overall resistance in the circuit. These arrangements are called series and parallel circuits. Fig. 2(a) illustrates two resistors connected in series and Fig. 2(b) shows the resistors in a parallel arrangement.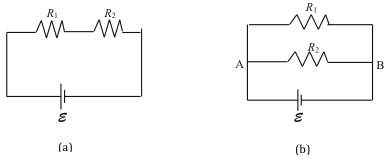

Figure 2: Resistors in series and parallel arrangements

In order for charges to move in a conductor, there must be a potential difference across the conductor, and there must be a complete path leading away from and back to the source of emf (

in Fig. 2). In the series arrangement shown in Fig. 2(a), the current I in the circuit goes through each resistor. If we compute the potential drop ΔV₁ across R₁ using Ohm's Law, it is

ΔV₁ = IR₁.

Likewise, the drop across R₂ is

ΔV₂ = IR₂.

The potential drop across both resistors is

ΔV = ΔV₁ + ΔV₂

which is equal to

. One can think of the applied voltage

being divided between the two series resistors R₁ and R₂. In the parallel arrangement shown in Fig. 2(b), the current divides at the junction A and recombines at junction B. Therefore, the current through R₁ and R₂ will be different. Notice that in this case

ΔV = ΔV₁ = ΔV₂.

That is, the potential drop across each resistor is the same. Using algebra, the relationships for determining equivalent resistance R_eq for resistors in series and/or parallel can be derived.

( 1 )

Series R_eq = R₁ + R₂ + . . .

The equivalent resistance is the sum of the individual resistances.

( 2 )

Parallel

R_eq

R₁

R₂

+ . . .

The reciprocal of the equivalent resistance is the sum of the reciprocals of the individual resistances.

Measuring Current and Voltage

Ammeters are used to measure the current flowing in a circuit. To do so, the ammeter should be connected in series with the circuit element through which you want to measure the current. Introducing an ammeter into a circuit should not affect the flow of current in the circuit and, therefore, ammeters have very low resistance. Voltmeters are used to measure the potential difference or voltage drop across a circuit element. To do this, the voltmeter should be connected to the two points across which you want to measure the potential difference. In other words, the voltmeter should be connected parallel to the circuit element. Voltmeters should not affect the current flowing through the circuit element and, therefore, voltmeters have high resistance. This prevents current from flowing through them.

Reading the Resistor Code

The resistance of most ceramic resistors can be determined from the colored bands printed on the resistor. Each color represents a digit from 0 to 9.

black	0	green	5
brown	1	blue	6
red	2	violet	7
orange	3	gray	8
yellow	4	white	9

The first two bands indicate the mantissa of a number in scientific notation; the third indicates the power of ten. The fourth band indicates the tolerance or the uncertainty expressed as a percentage in the value of the resistance (gold: ±5%, silver: ±10%, no 4th band: ±20%). Therefore, in order to know which end of a resistor to start from when reading the color code, it is useful to remember that the 4th band, if present, is metallic in color (gold or silver). If regular colors are present instead of these metallic bands, sometimes the color bands will be spaced differently or are closer to one end of the resistor to help indicate which end to start reading from. We will not be concerned with five-band resistors in this lab. If a fifth band were present, the first three bands indicate the mantissa, the fourth indicates the power of ten and the fifth indicates the tolerance (as brown, red, orange, yellow, or gold). See the example in Fig. 3 below.

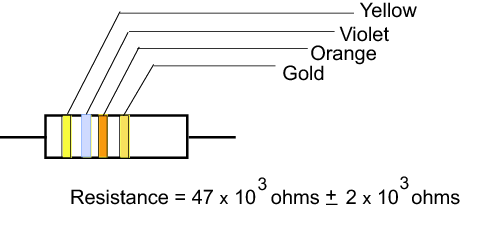
Figure 3: Reading the color code

Objective

The objective of this experiment is to use Ohm's Law to determine the resistance of several individual resistors and the equivalent resistance of series and parallel combinations. You will apply various voltages across the resistor (or circuit) using a power supply, and measure the current I through the resistor and the voltage ΔV across the resistor for each setting of the power supply. From a plot of ΔV vs. I, you will determine the resistance. You will compare the measured value of the resistance with the manufacturer's value.

Equipment

PASCO circuit board with two unknown resistors
DC power supply—adjustable from 0 to 5 V
Two hand-held multimeters
Connecting wires

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

You will set up a simple DC circuit with a single resistor and measure the current flowing through the resistor and the potential difference across it. From a plot of voltage versus current you will determine the resistance of the resistor. You will repeat this process with the second unknown resistor. You will use the two unknown resistors to set up a series combination and experimentally determine the equivalent resistance of the combination and compare it to the theoretical equivalent resistance. You will connect the two resistors in parallel and find the equivalent resistance of this parallel combination and compare this equivalent resistance to the theoretical equivalent resistance.

Procedure A: Determining Resistor Value Using Color Code

Enter the color of the four bands for the two resistors in Data Table 1.

Determine the resistor value for the resistors, and enter these values in Data Table 1. You will use these values as the expected or manufacturer's values when comparing with the experimental values.

Checkpoint 1:
Ask your TA to check your reading of the color code.

Procedure B: Determining R₁

To determine the resistance, you will set up the following circuit. You will use the Pasco Universal Interface as the adjustable power supply. Connect wires from the Interface output 1 as shown for the power supply, and open the appropriate Capstone file for DC circuits and Ohm's Law.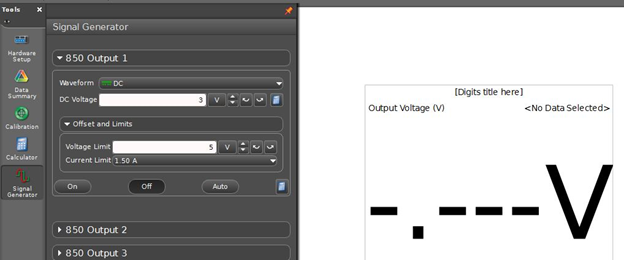

Figure 4a

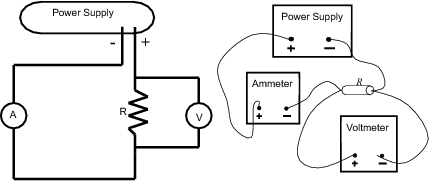
Figure 4b: Circuit diagram for Procedure A

Fig. 4a shows the circuit diagram and schematic for connecting a single resistor in series with the power supply and ammeter. In Fig. 4a,

represents a multimeter as an ammeter and

represents a multimeter as a voltmeter. You will use the circuit board shown in Fig. 5 below. The connection points are numbered in the schematic of the circuit board shown in Fig. 5(b). Refer to these numbers as you make the connections for each part of the lab.

Figure 5: Photo and schematic of circuit board

Fig. 6 below show the connections for each individual resistor using the circuit board. To provide clarity, the connecting wires in this and other subsequent diagrams have been drawn with different colors. These colors do not represent the true colors of the connecting wires you will be using.

Figure 6: Circuit diagram for the 100-Ω resistor

Make sure the power supply is turned off.

Connect the circuit shown in Fig. 6 for the 100-Ω resistor.

Precaution: If the multimeters are not set to the proper scale, it can damage the meters. Before you turn the power supply on, your TA must check your circuit.

Checkpoint 2:
Ask your TA to check your circuit and multimeter settings.

Set the power supply to deliver 3 V. Record the ammeter and voltmeter readings on your worksheet. Record the actual voltmeter reading and not the value on the power supply as these two readings might be slightly different.

Increase the power supply output in steps of 1 volt and record the ammeter and voltmeter readings on your worksheet, for a total of five different voltmeter readings.

Construct a graph of ΔV versus I using Excel. See Appendix G.

Use the trendline option in Excel to get the best fit line and determine the resistance from the slope of the graph. See Appendix H.

Compute the percent error between the manufacturer's value of the resistance (from Data Table 1) and the experimental value. See Appendix B.

Checkpoint 3:
Ask your TA to check your chart, calculations, and Excel graph before proceeding.

Procedure C: Determining R₂

Disconnect the first resistor and connect the second resistor as shown in Fig. 7.

Figure 7: Circuit diagram for the 33-Ω resistor

Repeat steps 5 through 9 with this second resistor and complete Data Table 3 on the worksheet.

Compute the percent error between the manufacturer's value of the resistance (from Data Table 1) and the experimental value.

Checkpoint 4:
Ask your TA to check your chart, calculations, and Excel graph before proceeding.

Procedure D: Determining Equivalent Resistance—Series Arrangement

Connect the two resistors you used before in a series arrangement. Connect one multimeter in series with the two resistors to read the current flowing in the circuit. See Fig. 8.

Figure 8: Connections for the series circuit

You will use the other multimeter as a voltmeter for measuring the potential difference across the series combination (as shown in Fig. 8), and then across each individual resistor R₁ and R₂. See Figs. 9 and 10 below.

Figure 9: Measuring potential difference across the 100-Ω resistor

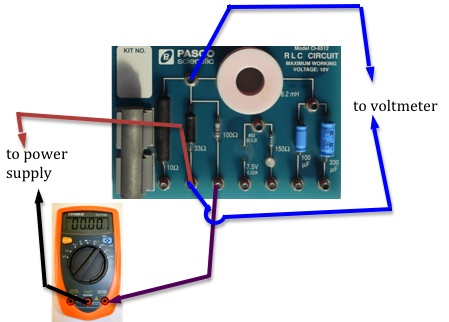
Figure 10: Measuring potential difference across the 33-Ω resistor

Checkpoint 5:
Ask your TA to check your circuit before proceeding.

Set the power supply to deliver 3 V. Record the voltmeter reading across the combination and the ammeter reading in the first two columns in Data Table 4 on the worksheet.

Measure ΔV₁ and ΔV₂, the potential drops across R₁ and R₂, respectively. Enter these in columns 3 and 4 in Data Table 4 on the worksheet.

Repeat steps 14 and 15 for four more readings of the power supply.

Use the first two columns of Data Table 4 to draw a graph using Excel and determine the equivalent resistance of the series combination from the slope of the graph.

Compute the theoretical equivalent resistance of the series combination using Eq. 1and the values from Data Table 1.

Compute the percent error between the measured and calculated values of the equivalent resistance. Record this on the worksheet.

Use the data in columns 3 and 4 of Data Table 4 to determine the total voltage across the series combination. Enter these values in the same data table.

Compare the measured and calculated total voltage drop across the series combination by computing the percent difference between the two values. Record these in Data Table 4.

Checkpoint 6:
Ask your TA to check your chart, calculations, and Excel graph before proceeding.

Procedure E: Determining Equivalent Resistance—Parallel Arrangement

Connect the two resistors you used before in a parallel arrangement. Connect the voltmeter to measure the potential difference across the parallel combination. See Fig. 11 below.

Figure 11: Connection for the parallel circuit

You will use the second multimeter as an ammeter to measure the current I flowing out of the power supply, as well as I₁ and I₂, the currents flowing through R₁ and R₂, respectively. To do this you will first connect the ammeter in series with the power supply (as in Fig. 11) to measure I. You will then disconnect the ammeter and connect it, first in series with R₁ (see Fig. 12) and then in series with R₂ (see Fig. 13) to measure I₁ and I₂.

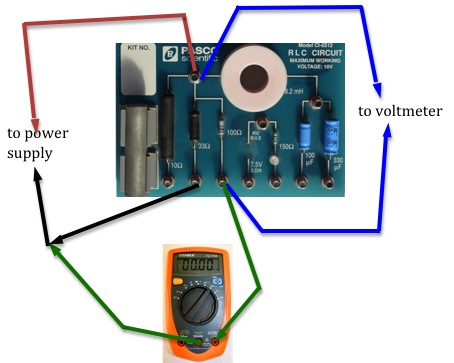
Figure 12: Measuring current through the 100-Ω resistor

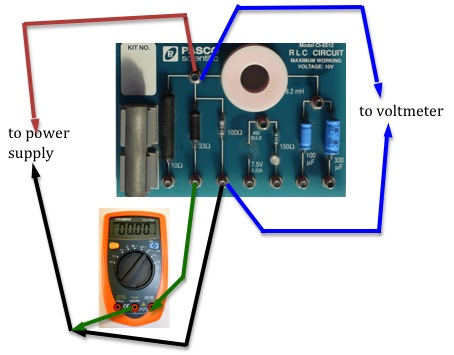
Figure 13: Measuring current through the 33-Ω resistor

Checkpoint 7:
Ask your TA to check your circuit before proceeding.

Set the power supply to deliver 3 V. Record the voltmeter reading in the first column in Data Table 5 on the worksheet.

Measure I, I₁, and I₂, the currents flowing from the power supply, and through R₁ and R₂, respectively. Enter these in columns 2, 3, and 4 in Data Table 5 on the worksheet.

Repeat steps 23 and 24 for four more readings of the power supply.

Use the first two columns of Data Table 5 to draw a graph.

Then use the trendline option in Excel to draw the best fit line and determine the equivalent resistance from the slope of the graph.

Compute the theoretical equivalent resistance of the parallel combination using Eq. 2 and the values from Data Table 1.