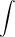Impulse, Momentum, and Energy – Concepts

Introduction

Newton expressed what we now call his second law of motion, not as F = ma, but in terms of the rate of change of momentum of the object dp/dt. In this more general and powerful form, the law states that when an unbalanced force acts on a body during a finite but short time interval, the change in the object's momentum depends on the product of the force and the time interval for which the force acts. The quantity Fdt is defined as Impulse, and the relationship between the change in momentum and the Impulse is sometimes referred to as the Impulse-Momentum Theorem. It states that the integral of the force with respect to time is equal to the change in momentum of the object.

Discussion of Principles

Impulse-Momementum Theorem

When an unbalanced force F_net acts on an object for a time interval Δt, the momentum of the object will change over this time interval. If p_i and p_f are the initial and final momenta at the start and end of this time interval respectively, then Newton's second law can be written as

( 1 )

F_net Δt = Δp.

The product F_net Δt, when summed over several small time intervals, is the integral of F_net dt, and is defined as the Impulse I.

( 2 )

I =

t_f	F_net dt

t_i

= p_f − p_i

Note that impulse is a vector quantity and has the same direction as the change in momentum vector. Figure 1 is a graph of the net force versus time. When the force is constant over a time interval, then the integral of F_net over the time interval is the area of the rectangle under the force line and bounded by the two time values. This is shown by the shaded region in Figure 1a. The example in Figure 1b is for a non-uniform force acting over an interval of time. In this case, the impulse would again be the area under the force-time curve as indicated by the shaded region.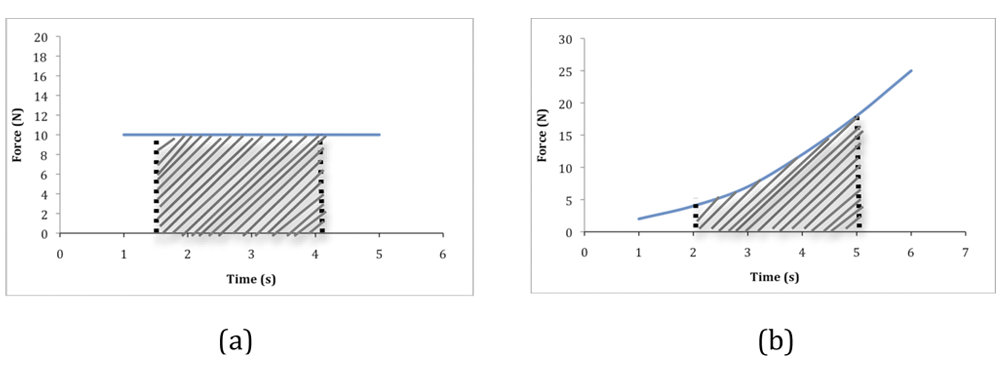

Graph of net force versus time in two parts. Part a shows a line of net force at 10, from one second to 5 seconds. The area from 1.5 seconds to a little past 4 seconds is shaded. Part b shows a curve beginning at 1 second and ends at 6 seconds. It moves upwards from about 2.5 to 25 net force. The area between two and five seconds is shaded.

Figure 1: Impulse as area under force-time curve

Work-Energy Theorem

The simplest form of the Work-Energy Theorem states that the change in kinetic energy of an object is equal to the total work done on that object.

( 3 )

ΔK = W

The work done can be divided into

W_C,

the work done by conservative forces like gravity, and

W_NC,

the work done by non-conservative forces like friction, so that equation 3 can be written as

( 4 )

ΔK = W_C + W_NC.

Since

W_C = −ΔU,

where

ΔU

is the change in the potential energy of the object, this can be rewritten as

( 5 )

ΔK + ΔU = W_NC

( 6 )

W_NC	=	(K_f − K_i) + (U_f − U_i)
	=	(K_f + U_f) − (K_i + U_i)
	=	(E_f − E_i)

where

E_i

is the initial value of the total mechanical energy of the object, and

E_f

is the final value of the total mechanical energy of the object. Therefore,

( 7 )

W_NC = ΔE.

equation 7 states that the total change in the mechanical energy of an object is equal to the work done by non-conservative forces.