Uniform Circular Motion – Concepts – Alternate Lab

Discussion of Principles

Part 1: Experimental Determination of Mass

The principle behind this experiment is that the weight of the hanging mass provides a tension that will provide the centripetal force for the swinging mass. Thus, for a mass moving in a horizontal arc, the weight of the hanging mass, m_hg, is equal to the centripetal force on the stopper,

M_s

v²

The speed of the moving mass can be related to the period of rotation and the radius of the path. Since speed is distance over time for constant speed, the distance of a circular path (the circumference, 2πr) divided by the time to travel the path (the period, T ) gives the speed:

( 1 )

v =

2πr

So the centripetal acceleration is

( 2 )

a_c =

v²

4π²r

T²

In this case, the radius of the path will be L, the length of string between the end of the tube and the stopper. Note that the centripetal force is being provided by the tension in the string necessary to support the weight of m_h. That is,

( 3 )

F_c = F_T = m_hg,

which yields

( 4 )

m_hg = M_sa_c.

This will be useful for calculating M_s from the slope of the trend line.

Part 2: An Alternate Method

In Part 1, an approximation is being made that the only force acting on the stopper is the tension in the string, and so the tension equals the centripetal force. In reality, gravity plays a role in the process as well. The string will actually be at an angle, as shown in Figure 1, rather than purely horizontal. In this case, the tension force (calculated with m_hg), is the hypotenuse of a right triangle, where the vertical side is the gravitational force on the stopper, M_sg, and the horizontal component is the centripetal force,

M_s

v²

A string runs through a vertical tube with a mass hanger on the end hanging below the tube and a rubber stopper on the end extending to the right of the tube, just slightly below the horizontal. The angle between the string with the stopper and a line indicating the horizontal is labeled theta. An arrow beneath the part of the string with the stopper points from the stopper towards the tube and is labeled as vector T. An arrow above the line indicating the horizontal points from the hanger toward the tube and is labeled with an equation indicating the net force vector equals the mass of the stopper times the centripetal acceleration vector. An arrow beneath the stopper points downward and is labeled with an equation indicating the force vector F sub g equals the mass of the stopper times the gravity vector. An arrow beside the mas hanger points downward and is labeled with an equation indicating the force vector for the hanger equals the mass of the hanger multiplied by the gravity vector.

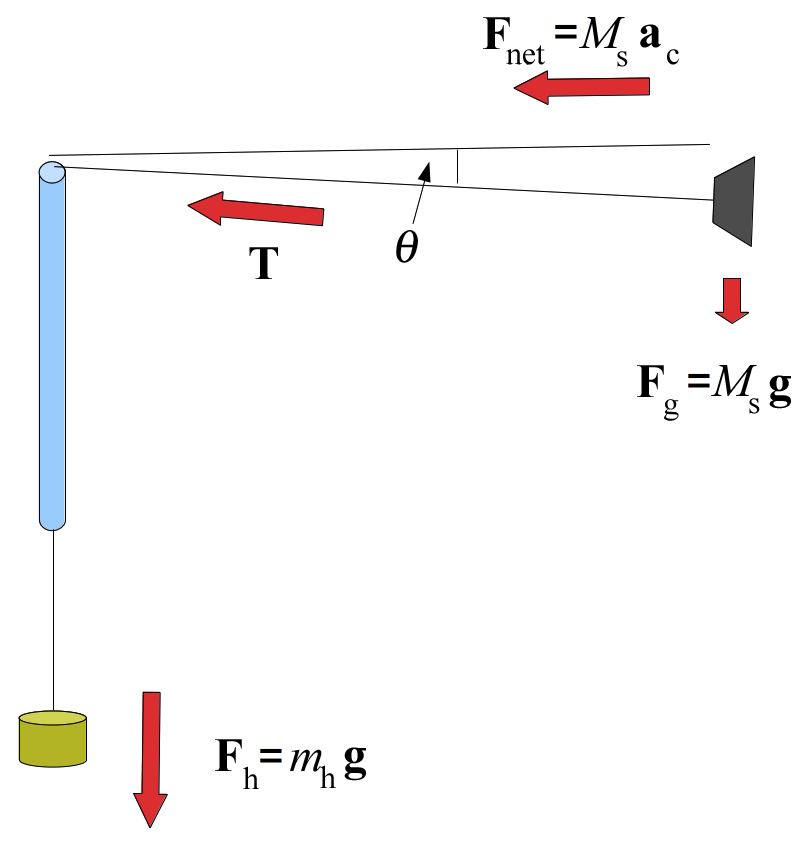
Figure 1: Including the force of gravity on the stopper

This means that when you include gravity, the centripetal force term, M_sa_c, is actually equal to only the horizontal component of the tension,

m_hg cos(θ).

( 5 )

M_sa_c = m_hg cos(θ)

The easiest way to determine the angle is to pause the video at a point where you can clearly see the angle θ and hold a small protractor up to the screen.