Standing Waves in an Air Column

Purpose

•
To observe resonance of sound waves in an air column open at one end and closed at the other.
•
To determine the speed of sound in air and the effect of the air temperature on that speed.
•
To examine the reflection of sound waves at the closed and open ends of a tube.
•
To study the effect of the tube length on the resonance frequencies produced.

Equipment

Virtual Sound Waves simulation
VPL Grapher
Pencil

Simulation and Tools

Open the Sound Waves simulation to do this lab. You will need to use the VPL Grapher to complete this lab.

Explore the Apparatus/Theory

Use Figure 1 as a reference to identify various parts of the apparatus.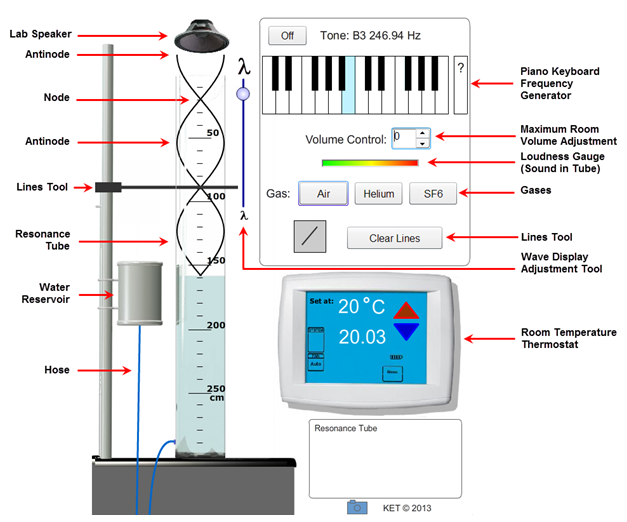

A resonance tube is marked every 50 cm down for a total height of 300 cm. A speaker sends a sound wave down into the tube. The start of the wave is labeled Antinode, with a node marked at 20 cm and an antinode at 50 cm. A black line labeled Lines Tool extends across the tube from a nearby stand. A water reservoir is connected to the cylinder. From the bottom of the water reservoir is a hose that extends down into the bottom side of the resonance tube. To the right of the resonance tube is a control panel that contains an off button, a piano keyboard frequency generator, a maximum room volume adjustment, and a loudness gauge for sound in the tube. There are gas options of air, helium, and SF6. A lines tool is available along with a button to clear lines. In between the resonance tube and the control panel is a sliding wave display adjustment. Beneath the control panel is a temperature control for the room set at 20 degrees C, displaying the current temperature of 20.03.

Figure 1

The Virtual Sound Waves apparatus allows you to observe standing sound waves in a closed air column. By "closed," we mean by convention that the tube is open at one end and closed at the other. Ours is open to the ambient air at the top and closed at the bottom by the surface of a column of water. You can adjust the length of the air column, L, the frequency of the sound, f, and the temperature of the air, T (°C). You can also replace the air with helium or sulfur hexafluoride, SF₆. A rubber hose connects a reservoir of water to a graduated cylinder. Lowering the reservoir allows water to flow from the cylinder into the reservoir. Try it. Raising and lowering the water level adjusts the length of the air column above it. It is the formation of standing sound waves in this column that we are interested in. (The ~~picky~~ observant student will notice that our reservoir appears too small to hold as much water as it needs to. In (virtual) reality, you're looking at an end-on view of an oval rather than a circular reservoir. That's my story, and I'm sticking to it.) Since our air column is filled with ambient air, adjusting the Room Thermostat thermostat icon

adjusts the temperature of the air column. Try adjusting the air temperature. When you finish, return the temperature to 20°C. We can also swap two other gases for our ambient air. In a real lab, that would be a problem for students. Your body will let you breathe helium until you collapse without your knowing there's a problem. So always be careful when you breathe it from a balloon to make your voice sound funny. Many a tooth has been lost when someone suddenly hit the floor. If you Google sulfur hexafluoride, you'll see some amazing videos of the properties of that gas. There's also some great misinformation about this on the Internet, too. "Googler" beware! Although we have three options for gases, we'll usually use the generic term "air column" in this document. We have one more thing to do before we plunge into our investigations. We need to set the minimum and maximum room volumes (loudness) so that you can perform the experiment without damaging your ears or bothering anyone around you. Its maximum value is adjusted using the Volume Control. We'll start with the room volume as low as possible and work from there. We'll use the term room volume to refer to the loudness of the amplified sound you hear with your computer speaker or headphones and the term tube volume to refer to the loudness of the sound in the resonance tube.

Caution:
If at any time you hear a sound that's too loud, click the Off button at the top of the screen. Be sure to get assistance if you have trouble with this. You don't want to damage your hearing. Also, be careful with headphones. When you first turn on the sound, be sure to have your headphones away from your ears. Once you've determined that the sound seems OK, you can carefully put your headphones on. If you can't lower the headphone volume adequately, you should use speakers instead. It would be better to use just the Loudness Gauge rather than damaging your hearing.

You need to adjust your computer's system sound level first. This is not set within the lab environment. It's set using your computer's controls. Seek assistance if necessary. Adjust your computer's system sound level to

its lowest nonzero setting for headphones.
near the middle of the range for speakers.

•
If you use headphones or external speakers to listen to audio, plug them in.
•
Drag the water reservoir all the way to the top.
•
Set the room volume setting at 5 in the lab control panel.
•
Play the "C4" sound frequency on the piano. It's near the middle. You should see the speaker at the top start to vibrate, but you should hear little, if any, sound.
•
The Loudness Gauge should look something like this: . This represents the tube volume.

•
Adjust the volume on your computer until you can just hear a quiet sound. You're hearing middle C. It doesn't sound like that note as played on any musical instrument since there are no overtones present. It's just a pure, single-frequency sound. As you can see from the display, the C4 note has a frequency of 261.63 Hz. A piano typically has eight octaves. Thus, it has eight C's. C4 is the fourth one from the bottom.
•
Quickly drag the reservoir until the water level is at about 50 cm. You'll hear the room volume rise and then fall as the water level passes approximately 17 cm. If that peak sound was uncomfortably loud, you need to reduce the computer system volume somewhat and try again. If it was not loud enough, try adjusting the room volume setting in the lab control panel. If necessary, you can adjust your computer system volume.
•
Continue raising and lowering the water level in this way until you get the volume adjusted to a comfortable level. The target is to be able to hear the sound faintly when the water is at the top and the Loudness Gauge looks like the figure above, while also hearing a louder but comfortable maximum loudness when the water is at about 17 cm.
•
There's no need to have the room sound on when you're not adjusting the water levels or making readings. It does tend to get annoying very quickly. You can set the room "Volume Control" to 0 to turn off the room sound at any time. The speaker above the tube will continue to play, and there will still be sound in the tube. You just won't hear it. Is that clear? The "Volume Control" controls what you hear—the room sound. The volume of the speaker over the tube will never change unless you turn it Off. Surprisingly, the sound in the tube, the tube volume, will change according to how we adjust various settings in the apparatus.
•
The Loudness Gauge measures the actual tube volume. When this volume is at its maximum, the gauge will look like this: . You'll frequently need to adjust the apparatus in some way to produce the loudest possible sound in the tube. Of course, when the tube volume is loud, the room volume will be, too.

Resonance of Sound in an Air Column

Make sure that you have air in the room (green background). Set the air temperature to 0°C. Drag the reservoir to its highest position and play C4. At any instant, the sound you're hearing was emitted just a fraction of a second before you hear it. Sounds produced a bit earlier have already reached you and jiggled your eardrums. Sounds produced a bit later have yet to reach you. Thus, you're hearing the sound produced at a certain earlier instant. Actually, you're hearing only a small part of that sound since the sound moves off in all directions, dropping off in intensity as it propagates in three dimensions. Now adjust the water level to about 17 cm. The volume reaches a maximum at about that point. So where's all that sound coming from? Actually, it's more like when. (More on this in a moment.) This would be a good time to adjust the "Volume Control" to zero! Drag the wave display adjustment slider until the wave display behind the water looks something like Figure 2.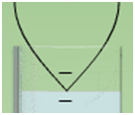

The top end of the resonance tube is shown. Water is inside and filled up to a point between the first and second mark. An antinode is above the tube. There is a node at the top of the water inside of the tube where the wave ends.

Figure 2

The wave display, which only appears at 0°C and multiples of 10°C, is helpful in visualizing what's happening in the tube. It provides a transverse wave representation of the longitudinal waves in the tube. You can do fine adjustments with the up and down arrows on your keyboard. Try it. (Yes, it's a bit counterintuitive. Moving the slider upward increases the wave display wavelength, making the wave expand downward.) Figure 2 shows the shortest air column that will produce resonance (the magnified sound) for a frequency of 261.63 Hz. This length is 1/4 of the wavelength of this sound in air at 0°C. One-fourth of a wavelength is the shortest wave that satisfies the boundary conditions for a standing wave in a closed air column. By boundary conditions, we mean the conditions necessary at certain key positions in the medium for resonance to occur.

The boundary conditions for standing waves in a closed air column are that an antinode exists at the open end and a node exists at the closed end. The amplitude of the longitudinal sound wave and corresponding transverse wave displayed is largest where the air has its greatest motion and lowest pressure—an antinode. The amplitude is smallest where the air has its least motion and greatest pressure—a node.

(In this document, the terms "node" and "antinode" will always refer to the displacement of air molecules. At a displacement node, the air molecules do not move relative to where they would be when no wave is present (bottom of Figure 2). In a displacement antinode, the molecules are moved a maximum distance relative to where they would be when no wave is present (top of Figure 2). The other use of the terms refers to pressure. At a pressure node, the pressure is always equal to the pressure that would exist when no wave is present (top of Figure 2). At a pressure antinode, the pressure differs by a maximum amount relative to the pressure that would exist when no wave is present (bottom of Figure 2). Note that these two are the reverse of each other.) You've probably noticed that the amplitude of the transverse wave also varies as you move toward and away from standing wave conditions. This also corresponds to the behavior of the actual longitudinal wave in the tube. When resonance occurs, most of the sound entering the air column is found to reflect back and forth between the two boundaries—the open end and the closed end—rather than just exiting the tube as it did earlier. As a result, energy from waves produced over a period of time is present in the tube at a given moment, and the sound that does escape the tube is greatly amplified. OK, OK, I can see that you're upset about the wave sticking out of the top of the tube. That's not an error. When a sound wave hits the water's surface, it's not surprising that it reflects back upward, but what about the open end? We need to know more about reflection. Suppose our speaker moved quickly downward just once. It would compress a small region of air, which would quickly expand into the surrounding uncompressed regions and, as a result, compress the air just beneath it. We'll ignore the effects on air in other directions. The newly compressed region would then expand and repeat the process, and so on. This compression "pulse" would continue down the tube. Note that it's not the air that's moving down the tube but rather the disturbance of the air, the moving region of compression of the air in the tube. When this pulse arrives at the water, it has to slow to a stop. So at some instant, we have a region of compression at the bottom that can go no further. It reflects back up the tube by expanding into the region above, and so on. So the bottom of the tube is a displacement node—the molecules there are fixed because they have no place further down to go. And it's also a pressure antinode—maximum pressure variation. Now the compression heads toward the open end of the tube. The air outside the tube is kept at ambient pressure by the large body of ambient air that can move toward and away from the opening as needed. As the pulse reaches the top of the tube, the compressed air rapidly expands out into the lower density ambient air and, due to its inertia, overshoots its mark and becomes less dense. That is, the area at the top of the tube is converted from a compression to a rarefaction. Ambient air rushes back into this lower pressure region and, due to its inertia, produces a compression that makes its way back down the tube to repeat the process. So the air at the bottom is relatively stationary, and the air at the top has large amplitude motion in and out of the tube. It's sort of like a very light spring attached to the bottom of the tube. If you tap it on the top, the compression wave will travel down the tube and reflect back up. The section of the spring at the top is free to move with a large amplitude. The lower end of the spring remains in place. That was all about a single pulse. What about the continuous sound provided by our speaker? The plot thickens. With a speaker diaphragm moving with sinusoidal motion, waves are continuously sent down the tube and back with many compressions and rarefactions occupying the tube all at once. For most frequencies, there would be chaos in the tube. But for any frequencies with a corresponding wavelength such that the length of the tube is

n +

λ,

where n is an integer, the waves will interfere so as to form a standing wave pattern. Where were we? Oh yeah. We were worried about the waves extending out of the top of the tube. The water surface at the bottom produces a well-defined node as described above. But at the top, all that air rushing in and out effectively extends the length of the tube. So the position of the antinode, which lies beyond the end of the tube, is less clearly defined and not just at the end of the tube. The wave display shows its approximate location. You'll find it experimentally later.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

I. Finding the Wavelength and Wave Speed from the Spacing of Nodes

We'll continue with the same conditions—room thermostat set to 0°C, air in the tube, C4 selected, and the wave display set for a node at about 17 cm as in Figure 2. Turn the volume on so you can hear the sound. Drag the reservoir as far down as it will go. As the air column lengthens, you should hear three more pulses of maximum loudness. Each of these indicates air column lengths that satisfy our two boundary conditions. That is, they indicate additional nodes. See Figure 3.

On the left is a vertical green tube with two black lines inside that crisscross each other. There is an antinode above the tube. To the right of the tube is a horizontal red line near the top, halfway between the top antinode and the first node. Extending downward from this red line are four lines labeled L1, L2, L3, and L4. L1 extends down to the first node. L2 extends down to the second node. L3 extends down to the third node. L4 extends to the fourth node at the bottom of the tube. The lines end at this node at the bottom of the tube.

Figure 3

The transverse wave revealed as the water falls provides a good record of these nodal points. But you'll probably need to do some adjustments. The loudness of the sound doesn't go from zero to its maximum at a point but rather over a range of several centimeters. So it's tricky to estimate just where the nodes are. By watching the Loudness Gauge while making fine adjustments to the transverse wave display, you should be able to make each of its four nodal points correspond nicely to the corresponding points of maximum loudness. You'll see that setting the bottom-most node yields the most precise results. Go ahead and do that fine tuning.

We know that for any wave,

( 1 )

v = λf,

where v is the wave velocity in m/s, λ is the wavelength in meters, and f is the frequency in cycles/sec (Hz). By measuring the spacing of the nodes using the centimeter scale on our tube, we can determine the wavelength of the C4 sound. We know that the frequency of C4 is 261.63 Hz. With this frequency and equation 1, we can determine the speed of sound in air at 0°C. If we label the locations of the four nodal points as shown in Figure 3, we can calculate the wavelength of our sound waves in a number of ways. In equations 2–4, each λ represents a calculation of the wavelength of our sound wave.

( 2 )

λ_a = 2(L₂ − L₁)

( 3 )

λ_b = L₃ − L₁

( 4 )

λ_c =

(L₄ − L₁)

We could calculate each one and then their average. But there's a better strategy. The absolute error—how much your answer differs from the correct value—will be the same for any of the measurements of L. The larger the total length measured, the smaller the relative error, that is, the smaller the absolute error divided by the length. So we'll use equation 4.

Using Table 1,

•
record your values for lengths L₁ and L₄.
•
calculate λ_c and record it as your wavelength value, λ.
•
calculate the velocity of sound in air at 0°C using equation 1
v = λf,
with λ.
•
calculate the percentage error between your experimental value for the velocity of sound in air at 0°C and the accepted value for the speed of sound at 0°C of 331.5 m/s.

II. The Effect of Air Temperature on the Speed of Sound

As you've learned earlier in the course, the volume occupied by a given mass of gas, and hence its density, varies with temperature. If the density of the gas occupying our tube changes with temperature, perhaps its velocity does too.

Reset the conditions in the tube again as before—room thermostat set to 0°C, air in the tube, C4 selected. Adjust the water level to L₄ so that you're hearing the amplified sound in the tube. Use the lines tool to put a marker at the L₄ (0°C) position. Record the value of L₄ (0°C).

If you have the room volume set to zero, adjust it to an audible level for the following. Increase the air temperature to its maximum value of 40°C. Listen for changes in the loudness. OK, you can reset the room volume if you like. As you increased the temperature, what happened to the loudness of the sound?

Adjust the water level up or down until you find the new location of the fourth node. It could be further up the tube or further down. You'll have to figure out which one is the new L₄ position.

a
Record the value of L₄ (40°C).
b
Has the wavelength of the sound increased or decreased?

Given that there is a change in wavelength, this must mean that either the speed or the frequency has changed, or possibly both. You probably didn't notice any change in the frequency, and this is reasonable given that the frequency of the sound is determined by the frequency of vibration of the speaker. So it's the velocity that must have changed.

Based on equation 1

v = λf,

, has the speed of sound increased or decreased with this increase in temperature? Explain your reasoning.

Let's determine the relationship between the speed of sound in air and the temperature of the air. We again need to determine the wavelength experimentally and then calculate the wave speed using equation 1 for each temperature setting. Just as before, we'll find λ_c from equation 4

λ_c =

(L₄ − L₁)

. Calculate and record this as your wavelength, λ, for each temperature in Table 2. Use Table 2 to find the velocity at each of the five temperatures given. We're looking for very small changes, particularly in the L₁ value. Patience is a virtue.

You should have found that the speed increased with temperature as predicted. To find the relationship, plot velocity vs. temperature. We'll use Celsius degrees, °C, for our temperature units. You should find a fairly linear graph with Grapher. Use manual mode and start both axes at 0. (Be sure to click in an empty cell after entering the last data point. Otherwise, it won't show up.) Sketch your graph on the grid in Figure 4. Take a Screenshot screenshot tool icon

of your graph and upload it as "soundwaves_vt".

A blank graph of Speed of Sound (m/s) on the vertical axis versus Temperature (degrees C) on the horizontal axis is shown. The vertical axis goes from 0.0 to 360.0. The horizontal axis goes from 0.0 to 40.0.

Figure 4

Write your equation in

y = mx + b

format.

Using the accepted values (for this apparatus) for the slope and y-intercept gives the equation

( 5 )

v = 0.679 T m/s + 329.9 m/s.

This is an empirical equation that works fairly well for a limited range of temperatures. To see how well your results compare to these accepted values, calculate the percentage error for your slope and for your y-intercept.

III. Determining the End Correction for the Tube

We found that our sound wave resonated in an air column that extended somewhat beyond the top of the tube. We now want to determine the length of this extra column of air, the "end correction." This end correction is represented by the dark rectangle at the top of Figure 5.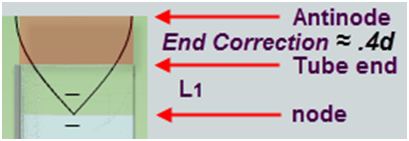

The top of a tube filled with water is on the left. There is an antinode above the tube and a node inside the tube at the top of the water in between the first and second mark on the tube. Between the labels for the antinode and the top end of the tube, L1, is the text End Correction is approximately .4d.

Figure 5

Knowing the wavelength of your C4 wave (at 0°C), you can compute the distance between the node and antinode in the figure. Knowing the distance L₁ from Table 1, you can compute the value (length) of the end correction from the top of the tube to the antinode above.

Determine the experimental value of the end correction.

By careful analysis, the resonating column of air is found to extend approximately 0.4 × diameter of tube. We will use this as the accepted value. The tube's diameter is 0.38 m.

Determine the theoretical value of the end correction, 0.4 × diameter of tube.

Calculate the percentage error between the experimental and theoretical values for the end correction.

Note that this end correction is considered a part of the standing wave even though it is outside the physical tube. Be sure to include it in any calculations involving the effective length of the resonating air column.

IV. The Effect of Air Column Length on Resonance Frequencies; Musical Instruments

Let's finish up with something a bit more musical! If there came a time when we needed to leave this planet to set up our civilization elsewhere, we would need to build a pretty large musical ark to carry all the different wind instruments that people, animals, and inanimate nature have invented. They all work based on the same basic principles as our glass tube, but they are way more complex. And even the performer is part of the instrument. If you'd like to know more, please check out "The Physics of Music" by David Lapp. With the exception of a few instruments such as the bugle, all wind instruments play a fundamental frequency along with other higher pitches that can be produced by changing the effective length of the resonating air column. So where do the notes come from? A wind source such as your lungs or an actual natural wind provides a supply of moving air, which passes into or, in the case of whistling, out of the instrument. The airflow is interrupted by some sort of "reed" that interrupts the flow of the air at a frequency controlled by the dimensions of the instrument. We want to investigate how the resonance frequency is related to the length of the resonating air column. The dimensions of the tube as well as the placement of openings along its length determine the frequency of the wave that will resonate in the tube and influence the frequency of the reed.

To make life more comfortable for our musicians, we'll use a temperature of 20°C for this section. We'll also use 342.7 m/s and

0.15 m

for the speed of sound and end correction, respectively.

With no tone playing (click OFF), drag the water reservoir all the way to the top.

Drag the wave display slider all the way to the top.

Play C3. It should be barely audible, if at all.

Slowly drag the reservoir downward until the maximum volume is heard for the first time.

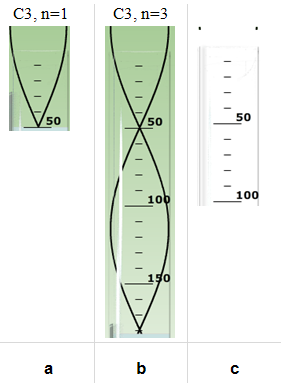
The top 50 centimeters of a tube labeled a has an antinode above the tube and a node inside the tube at 50. Above tube a is the label C3, n = 1. The top 180 centimeters of a tube labeled b has the first antinode above the tube and nodes at 50 and 180. The lines start apart at the top and intersect at 50 and 180. Above tube b is the label C3, n = 3. The top 100 centimeters of an empty tube is labeled c.

Figure 6

Adjust the wave display to match Figure 6a.

Carefully drag the reservoir downward until the sound becomes quiet and then reaches its second maximum.

Adjust the wave display, if necessary, to match Figure 6b.

At each of these two configurations and no others, the tube met the conditions for resonance for a C3 tone (130.81 Hz)—an antinode at the top and a node at the bottom. (A longer tube could produce further similar harmonics.) At all other positions, the waves are still reflecting up and down in the tube. There's just no resonance since the waves going up the tube are not properly synchronized with those going down. You've found that 130.81 Hz is a natural frequency for air columns of these two particular lengths. You first learned about this as a young child when you found that if you sloshed back and forth in the bathtub at just the right frequency, you could make massive waves. This was, of course, frowned on, leading you to abandon your physics studies until now. With a more sophisticated tank with vertical walls and one wall arranged to pulse at different frequencies, you can set up standing water waves that just remain still. That is, they don't travel from one side of the tank to the other. They just rise and fall in place. That's also what's happening in our tube at resonance. The conditions for a standing wave in a closed tube can be described mathematically as follows. For a closed tube with waves of velocity, v, resonance will occur at frequencies f₁, f₂, f₃, ..., with wavelengths λ₁, λ₃, λ₅, ..., given by the following equations.

( 6 )

λ_n =

( 7 )

f_n =

where

n = 1, 3, 5, ..., n =

the number of quarter waves that will exactly fit into the length, L.

Ex. For Figure 6a, we have a quarter wavelength in the air column, where

n = 1,

v = 342.7 m/s,

and

L = 0.51 m + 0.15 m = 0.66 m.

We'll use these values for

v (342.7 m/s)

and the end correction (0.15 m) in this development instead of your experimental values. From equations 6 and 7,

λ₁ =

4 × 0.66 m

= 2.64 m

f₁ =

1 × 342.7 m/s

4 × 0.66 m

= 129.81 Hz,

which is pretty close. Our λ₁ looks about right given the distance—about 1.32 m—we see between the two nodes in Figure 6b. And our f₁ is pretty close to the 130.81 Hz note we played.

So equations 6

λ_n =

and 7

f_n =

predict what wavelengths and frequencies will be needed for resonance just based on the wave speed and the length of the air column! Also notice that in equation 6, the "n" term allows only a quarter wavelength air column, a three-quarter wavelength air column, etc. This matches our boundary conditions. Figures 6a and 6b both contain waves of identical frequency and wavelength. A larger L value will only produce standing waves if some other odd number of quarter wavelengths will fit. But what will happen if we try a different frequency with the same initial length,

L = 0.66 m?

Reset the apparatus with C3 and

L = λ/4

as in Figure 6a.

Click D3, which is the next white key to the right. No resonance. And the result is the same for E3 and F3.

Repeat with every key until you find another note that produces strong resonance.

Record the second frequency producing resonance in an air column of length 0.66 m.

Don't move the wave display slider yet. Instead, in Figure 6c, draw the standing wave, with

n = 3,

that you think is present in this tube with this new higher frequency. The tops of the waves are provided to get you started. Think about how this new resonant frequency compares to C3. Is its frequency higher or lower than C3? Would its wavelength be longer or shorter? Look back at the discussion of boundary conditions in the exploration section. How could the G4 tone fit within the 66-cm length and still meet the boundary conditions?

Adjust the wave display slider to match your figure. You can then see if you were correct by moving the water reservoir up and down. You should see that you'll get resonance at both nodes! Make any corrections necessary to Figure 6c.

Take a Screenshot screenshot tool icon

of the upper end of the tube and upload it as "soundwaves_Figure6c".

How many quarters of C3's wavelength fit in this 0.66-m "tube"?

What did we find above for C3's wavelength?

How many quarters of G4's wavelength fit in this 0.66-m "tube"?

Using equation 6

λ_n =

, determine G4's wavelength.

Show your theoretical calculations of G4's wavelength and frequency using equations 6

λ_n =

and 7

f_n =

We stated above that the integer n in our equations was equal to the number of quarter wavelengths that fit within a given resonating length, L. It also represents something fundamental about the frequencies of the sounds that will resonate within an air column of a given length, L.

What do the two values for n in #16 and #18 tell you about the two frequencies? You can find out by considering the fact that for a constant velocity,

λ_C3f_C3 = λ_G4f_G4.

Show your calculations of the ratio of

f_G4

f_C3

This second frequency that the 0.66-m air column can "play" is the third harmonic frequency of the fundamental C3 note.

That is,

1st harmonic:      C3      f₁ = 130.81 Hz      fundamental frequency
2nd harmonic:      C4      f₂ = 261.63 Hz
3rd harmonic:      G4      f₃ = 392 Hz      1st overtone.

Because of the structure of the closed-ended tube, it cannot play any even harmonics because that requires the ability to create antinodes (or in the case of string, nodes) at each end. An open-ended tube can play all the harmonic frequencies just as a stringed instrument can. Actually, conical closed-tube instruments or instruments with flared ends are able to approximate the full set of harmonics. This is why musical instruments are not created based on some strict mathematical calculations. They are more of playable pieces of art or craftsmanship.

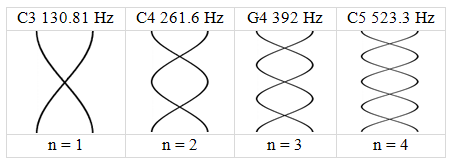
Four sound waves are shown. The first is labeled C3 130.81 Hz and n = 1. Shown are two antinodes and one node. The second wave is labeled C4 261.6 Hz and n = 2. Shown are three antinodes and two nodes. The third wave is labeled G4 392 Hz and n = 3. Shown are four antinodes and three nodes. The fourth wave is labeled C5 523.3 Hz and n = 4. Shown are five antinodes and four nodes.

Figure 7: Harmonics 1–4 for an open tube

Closed instruments such as closed flutes, recorders, and organ pipes will play only the odd harmonics. Open-tube instruments such as open flutes and pan pipes, which are open at each end, can play all harmonics, so you'd hear all four of the frequencies shown in
Figure 7. The equations matching equations 6

λ_n =

and 7

f_n =

for an open tube are slightly different.

( 8 )

λ_n =

( 9 )

f_n =

where

n = 1, 2, 3, ..., n =

the number of half waves that will exactly fit into the length, L. For a given note, would the dimensions of these tubes be the same as with our closed tubes? We'll leave that for you to calculate. Unfortunately, you can't test it with our apparatus. This difference in the harmonics that can be played by an instrument is one of the ways in which we distinguish between them when we hear them. These distinguishing characteristics of the sounds of different "instruments" is known as their timber (TAM-ber or TIM-ber) or tone quality. It's actually more subtle than just the harmonics they can play. Otherwise, all closed tubes of a given length would sound the same. If you listened to an orchestra's wind section all playing together, you might not know the names of the different instruments, but you could certainly distinguish one from another. This is due to the power of the sounds of the different harmonics that each produces. For example, a typical open flute plays the first and third harmonics very strongly, but the second is not so strong. After the third harmonic, the power gradually diminishes with a few strong harmonics here and there. A clarinet characteristically plays the first several odd harmonics at about even power, but the even harmonics are produced at somewhat less power. A bassoon typically rises in power from the first up to the fourth harmonic, stays steady, and then begins to diminish in power. The player of the instrument also plays some role in the tone quality. And speaking of the human input, you've probably observed that when you get a phone call on a not-so-great phone, it's hard to tell who's calling even if it's a close friend. That's because a better quality phone is one that can accurately reproduce the sound spectrum of the caller. And this works for both ends. A call will only be clear if both phones have good fidelity. In ancient times, a.k.a. the 50s and 60s, "records" often had the words "Hi Fidelity" prominently printed on their covers. And they sounded best if you played them on a good "Hi Fi." In a less musical case, if someone drops an object out of your view, you could very likely tell them whether it was, say, a screwdriver, a wrench, or a teaspoon. And if it was a wrench, you could probably suggest approximately how long it was. Finally, why is the buzzing sound that we're working with in this lab so unpleasant? I was puzzling on this and momentarily considered the possibility that a single frequency is not very common given that most sounds that we hear involve something that can produce a range of frequencies. Then it hit me. Bees, mosquitos, electric saws, dentist drills... Hmm. Beware the buzz!

1st harmonic:	C3	f₁ = 130.81 Hz	fundamental frequency
2nd harmonic:	C4	f₂ = 261.63 Hz
3rd harmonic:	G4	f₃ = 392 Hz	1st overtone.