Print

Module 7 – Ohm's Law

Introduction

In this experiment, you will study Ohm's Law, the most fundamental relation used in the analysis of electrical circuits. Ohm's Law relates the quantities of voltage, electric current, and resistance in one easy-to-use equation. This illustration provides you with an aid to help you remember the three forms of Ohm's Law. If you know two of the three quantities, it is possible to determine the third.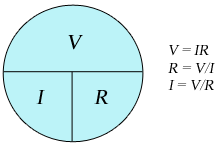
A circle divided into sections represents Ohm's Law. The top half of the circle is labeled with the letter V. The bottom half is split into 2 sections. One is labeled I and the other R. The following equations are given V = I*R, R = V/I, and I = V/R. The horizontal line of the circle represents the division needed if you are writing Ohm's Law to find R or I.
Figure 1
In the following information, you will study these three physical quantities as they relate to simple electrical circuits.

Simple Electric Circuit

The simplest electric circuit contains a source of electric power and a resistance. The power supply is a source of electrical energy, which is used to supply electric current that flows through the resistance in the circuit. A water pump analogy is often used to help illustrate the concept. The water pump creates a difference in pressure between the two ends of the pipe. This pressure difference causes the water to flow through the pipes as it moves from high pressure to low pressure. As the pressure is increased, the flow of water also increases.
A simple electric circuit has a wire running from the positive end of a power supply through a resistance, created by a resistor, to reconnect with the negative end of the power supply. A water pump has a pipe running from the pump through a resistance, created by a narrowing of the pipe, to reconnect to the pump on the other side.
Figure 2: Water pump and electric circuit analogy
In the case of an electric circuit, the power supply does not create a pressure difference; instead, it creates an electric field throughout the circuit. Locations in the circuit differ in electrical potential energy, and electric charges move from higher potential energy to lower potential energy. This movement of charge constitutes an electric current. Like pressure in the water pump analogy, an increase in electrical potential energy of the power supply increases the electric current. The power supply's voltage is a measure of the electrical potential energy across its terminals. In both cases, the current flow will decrease when the resistance increases, assuming that the electrical potential energy or pump pressure has not also increased.

Electric Current

Electric current is defined as the amount of charge that flows each second. As you can see in the illustration, an electric current can exist in wires, solutions, and even in the vacuum of a television tube. The unit of electric charge is the coulomb, so electric current has the unit coulomb per second (C/s); this is also called the ampere (A).
( 1 )
1
C
s
 = 1 A
Meters used to measure electric current are placed in line with the circuit components so that the same current flowing through the circuit also flows through the meter.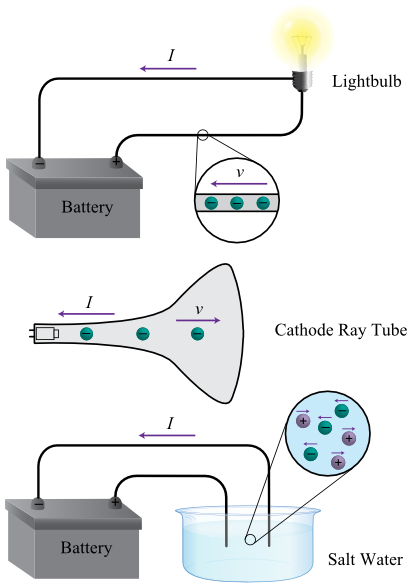
Three examples of electric current flow are shown. In the first example, a wire runs from the positive terminal of a battery to a lightbulb and then from the lightbulb to the negative terminal of the battery. Current flows from positive to negative. In the second example, electrons flow through a cathode ray tube. In the third example, a wire is connected at one end to the negative terminal of a battery, the other end immersed in a container of salt water. A second wire runs from the salt water to the positive terminal of the battery. Current flows from negative to positive.
Figure 3
It is interesting to note that the unit of electric current, the ampere, is one of seven fundamental units in the SI system of measurement.

Voltage

As you have seen, the voltage in an electric circuit is analogous to the pressure created by a water pump. More precisely, however, the voltage in an electric circuit is a measure of the amount of electrical potential energy per charge between two points in the circuit. Take a look at the illustration. Suppose you have an accumulation of electric charge (a battery or power supply). This electric charge will create an electric field that exerts an electric force on the charge located in the field. In our case, assume that the large positive charge is fixed, and that the small negative charge is able to move. The work required to move the negative charge will be the force required to overcome the electric attraction times the distance moved.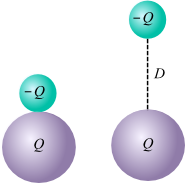
At one instant, a smaller negative charge is just touching a larger positive charge. At a later time, the negative charge has been moved a distance D away from the positive charge.
Figure 4
The negative charge will now have a potential energy equal to that work. The difference in potential energy between the starting and stopping points is called the potential difference, or voltage, across the points. The voltage between any two points in an electrical circuit is equal to the change in electrical potential energy per charge between the two points. For this reason, voltage is always measured across two points. The unit of potential difference, or voltage, is the volt (V). One volt is equal to one joule of potential energy difference per coulomb of electric charge.
( 2 )
1 V = 1
J
C

Resistance

Resistance is the opposition to current flow. In the water pump analogy, the more narrow the pipe, the less water will flow. Similarly, the greater the electrical resistance for a given voltage, the less electric current will exist. Consider the flow of electric charge through a conducting wire. As the charge begins to move, it collides with the atoms in the wire. This impedes the current flow. The more collisions, the greater the resistance to current flow. If each charge has greater potential energy, it will tend to move through the wire with greater kinetic energy as it "falls" from point to point, and the electric current will increase. In other words, the voltage and current are directly proportional. The amount of increased current for an increase of voltage depends on the resistance in the circuit. Ohm's Law summarizes these facts in a simple, easy-to-use equation.
Voltage is proportional to Current.

Voltage = Current × Resistance
( 3 )
V = IR
The unit of electrical resistance is the ohm (Ω); it is equal to 1 volt/ampere. The illustration demonstrates this proportionality between voltage and current. Notice that the slope of the line is equal to the value of the resistance in the circuit.
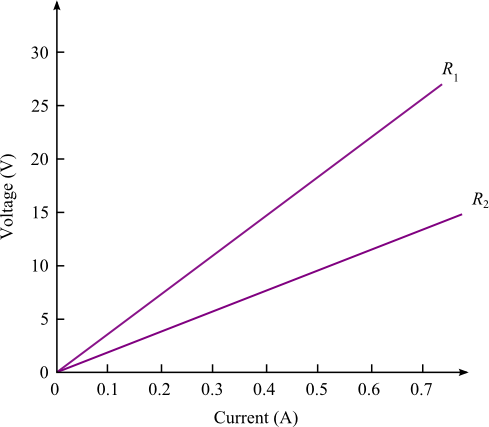
A graph of voltage versus current. There are two lines labeled R 1 and R 2 on the graph. Both lines start at the origin and slope upward, indicating an increase in voltage with increasing current. R 1 has a steeper slope than R 2.
Figure 5

Procedure

You will observe the experiment performed and fill in your data sheets.
1
Open the experiment instructions and worksheet.
2
After you have opened the instructions and worksheet, select and watch the Experiment Video (the Experiment Video is available in your course LMS).
3
Record your data in the worksheet. (You will need it for the lab report assignment in WebAssign.)

Copyright © 2012-2013 Advanced Instructional Systems, Inc. and Embry-Riddle Aeronautical University | Credits