Module 6 – Standing Waves

Introduction

A standing wave is a pattern which results from the constructive and destructive interference of two or more waves traveling in the same medium. Waves traveling through solid objects, such as a string, the ground, or air, will do so with a wavelength, velocity, and frequency that are determined by the medium in which they are traveling and the source producing the waves.

INTERFERENCE

Standing waves are possible through the phenomena of constructive and destructive interference. As waves pass each other, their energies—manifesting in wavelengths, amplitudes, and speeds—either interfere in a constructive manner, making the wave amplitude larger, or in a destructive manner, decreasing the resultant amplitude. The waves may be moving in the same direction or in opposition, as with a reflected wave. The final waveform is determined by how the waves interact. Pure tones have a smooth, sinusoidal waveform (first and second images in Figure 1). Complex tones are regularly repeating waveform, with a wavelength and frequency, but they do not have the smooth sine curve waveform (bottom image, Figure 1). The special case of both waves having the same speed, wavelength, and amplitude when they interfere is shown in Figure 2. These are pure tones.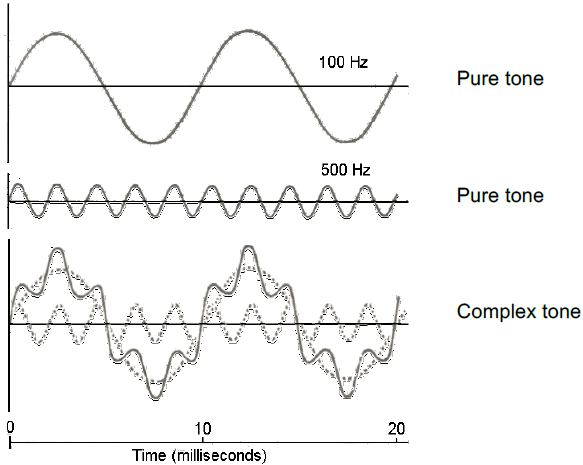

Figure 1: Complex tone produced from constructive and destructive interference of two pure tones of different frequencies (100 Hz and 500 Hz) and amplitudes.

NODES AND ANTINODES

All standing waves have certain special positions along the medium which are standing still, referred to as nodes. Antinodes are other special positions where the particles within the medium oscillate about their equilibrium position with maximal displacement. Standing wave patterns are always characterized by an alternating pattern of nodes and antinodes, with the number of nodes always being one more than the number of antinodes. Waves on strings are transverse waves. When a string is vibrating at its fundamental frequency, the wave pattern looks like the top image in Figure 2.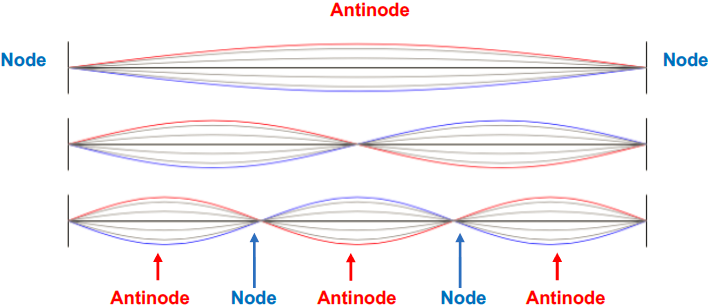

Figure 2

There is an antinode at the middle where the displacement of the string is at a maximum. There are nodes at the fixed ends of the strings where there is no displacement of the string. Although changing the wavelength can produce different standing waves, they can be produced only if the wavelength is a whole number multiple of half wavelengths. Notice the top image in Figure 1 is one-half a wavelength. The second image shows one full wavelength, the third, one and one-half (or 3λ/2) wavelengths. In short, for a string of length, L (with two fixed ends): L = n(λ/2), where n = 1, 2, 3, .... Fundamental: n = 1; L = λ/2; 1/2-wavelength fits into the length of the string (top image). Second harmonic: n = 2; L = λ; 1-wavelength fits into the length of the string (middle image). Third harmonic: n = 3; L = 3λ/2; 3/2-wavelengths fit into the length of the string (bottom image). Knowing the frequency of the oscillation, f and the wavelength of the standing wave, λ, allows the calculation of the speed of the wave, ν, on the string using the relationship ν = fλ. The velocity of a wave on a string is dependent on several factors, including the tension on the string (F) and its linear mass density (ρ). This relationship is: ν =(F/ρ)^1/2.

PROCEDURE

This experiment consists of three parts.

Open the experiment instructions and worksheet.

•
Standing Waves Experiment Instructions (HTML or PDF)
•
Standing Waves Experiment Worksheet

After you have thoroughly read the instructions and worksheet, open the experiment simulations in which you will conduct the experiment and collect your data.

•
Part I Simulation: Experiment link
•
Part II: Experiment link

Record your data in the worksheet. (You will need it for the experiment report assignment in WebAssign.)