Print

Module 2 – Newton's Second Law

Introduction

You have learned that all freely falling objects fall at the same rate, but that the force on any one object depends on its mass. This is because more massive objects require greater force to be accelerated the same amount as less massive objects. This is not hard to understand. It takes more push (force) to get the heavier car to accelerate than it does the less massive lawn mower.
A drawing of a man pushing a car and a drawing of the same man pushing a lawn mower. Above the man an arrow pointing to the right, which has the same length in both drawings and is labeled F. The car and shopping cart are both underneath arrows pointing to the right labeled a. The arrow labeled a is longer for the lawn mower than for the car.
Figure 1
In this experiment, you will continue your study of Newton's Second Law. You will experiment with a machine that allows you to attach a free falling body to another mass. By doing this, it is possible to slow the free falling object's rate of fall. In addition, it helps you to understand the relationship between force, mass, and acceleration more completely.

Modified Atwood Machine

Take a good look at Figure 2 below. Let's apply Newton's Second Law to this machine. Remember that the Second Law can be written as follows: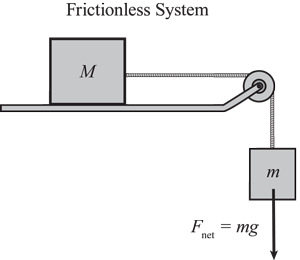
( 1 )
Fnet = ma
or
( 2 )
a =
Fnet
m
.
A drawing labeled Frictionless System. One box, labeled M is on a horizontal surface. A string is attached to this box, continues horizontally until it passes over a pulley. A smaller box, labeled m, is hanging from the other end of the string. An arrow points downward from the bottom of the smaller box. The equation F net = m g is given.
Figure 2
The "secret" to applying this relation to our machine is that you need to remember that while the force of gravity acts only on the hanging mass, it is applied to both masses. So the applied force is equal to the weight of the hanging mass, but this force is required to move a mass equal to the sum of the masses. Let's take a look at these two conditions.
Condition 1: Fnet = mg
Condition 2: a =
Fnet
(M + m)
The first equation simply quantifies the fact that the weight of the hanging mass is the only force causing the two masses to move. In addition to causing the hanging mass to fall, it creates a tension in the string, which pulls on the second mass. The second equation relates the rate of fall, the acceleration of the system, –a, to the total applied force on the two masses. If you substitute the first relation into the second, you obtain an equation for acceleration in terms of the acceleration due to gravity and the masses themselves. These variables are either known or can easily be measured. The rate of fall of mass m is:
( 3 )
a =
mg
(M + m)
.

Acceleration Revisited

Take a good look at equation 3
a =
mg
(M + m)
.
 for the system's acceleration again. Let's study the acceleration when we vary the masses.
( 3 )
a =
mg
(M + m)

M = 0 kg

When you remove the mass on the table, equation 3
a =
mg
(M + m)
.
 yields a = g. This is just the case we have for free falling objects. The hanging mass is not restrained by the mass on the table, so it will fall freely.

M is larger than m: M = 2 kg; m = 1 kg.

When the mass on the table is twice as massive as the hanging mass, equation 3
a =
mg
(M + m)
.
 yields a = (1/3)g. This makes sense too. The weight of the hanging mass is required to move three times the mass, so the acceleration is reduced to one-third the value. If you increase the table mass to 99 times the hanging mass, the acceleration becomes a = (1/100)g. When friction is introduced, the system is stationary, but without friction, the rate of fall is reduced significantly.

M is smaller than m; m = 2 kg; M = 1 kg.

When the hanging mass is twice that of the mass on the table, equation 3
a =
mg
(M + m)
.
 yields a = (2/3)g. In this case, notice that the system accelerates more quickly than the case when table mass was larger, but not as quickly as in free fall. As you increase the hanging mass, the acceleration of the system will get closer and closer to g. When the hanging mass is 99 times the mass on the table, the rate of fall will be (99/100)g or 0.99g.

Procedure

This experiment consists of three parts.
1
Open the experiment instructions and worksheet.
  • •
    Newton's Second Law Experiment Instructions (HTML or PDF)
  • •
    Newton's Second Law Experiment Worksheet
2
After you have thoroughly read the instructions and worksheet, open the experiment simulation in which you will conduct the experiment and collect your data.
3
Record your data in the worksheet. (You will need it for the lab report assignment in WebAssign.)

Copyright © 2012-2013 Advanced Instructional Systems, Inc. and Embry-Riddle Aeronautical University | Credits