Rotational Motion

Objectives

•
to study the basic concepts of rotational motion such as torque and moment of inertia
•
to validate the conservation of energy law

Equipment

a large, 6 inches in radius, aluminum disk attached to the rotary motion sensor
meter stick
set of small masses from 20 g to 50 g

•
The radius of the large-sized pulley is 2.387 cm.
•
The radius of the medium-sized pulley is 1.432 cm.

Introduction and Theory

In this experiment, we will study the effect of a constant torque on a symmetrical body. We will determine the angular acceleration of a disk. From this, we will measure its moment of inertia, which we will compare with a theoretical value. We will also study how energy is conserved in this sort of system. The apparatus for this experiment is shown in fig. 1. It consists of a large disk that is mounted on the PASCO rotary motion detector unit. The unit has several pulleys on it. We have a string that is wound on the pulley on which we hang various masses. The experiment will consist of winding the string up, and then allowing the mass to fall and unwind the string. During this, the angular velocity of the disk will increase to a maximum. When the mass reaches the bottom of the string, the rotating disk will wrap the string back up until the disk has zero angular velocity. The height that the mass reaches on its way up will be nearly the same as the starting point because energy is almost completely conserved. From all of this, you will measure the angular acceleration, determine the moment of inertia, and check if the Law of Conservation of Energy holds in this system.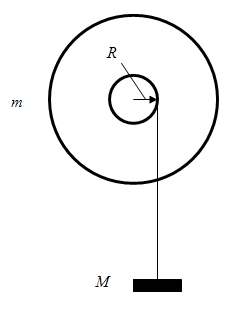

Figure 1: The experimental setup for the Rotational Motion lab

The basic equation for rotational motion is:

( 1 )

Στ = Iα,

where I is the moment of inertia in units of kg · m², τ is the torque in N · m, and α is the angular acceleration in units of rad/sec². For a uniform disk pivoted about the center of mass, the moment of inertia is

I =

mr²,

where m is the mass of the disk and r is the radius of the disk. Measure α and use it to calculate I, which you will need to compare with the theoretical value of I. A typical graph produced in DataStudio^® for this experiment is shown in fig. 2, below.

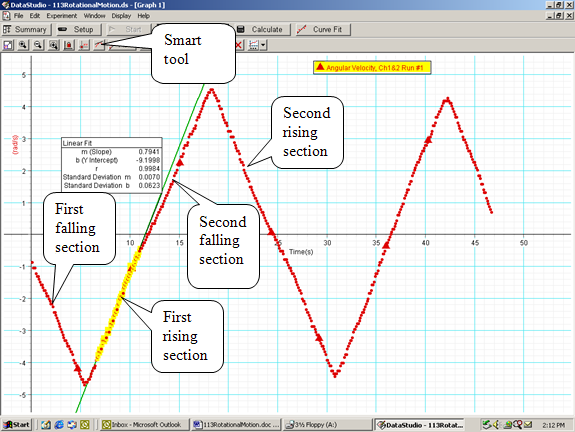
Figure 2: A sample file in DataStudio^®

Each section corresponding to

of the period of the recording represents a separate consecutive portion of the hanging mass motion: falling – rising – falling – rising – etc. It is easy to notice that the magnitude of the angular acceleration (α = slope of the angular velocity vs. time recording) is smaller when the mass M is falling than when it is rising. This effect is due to friction. When the mass M is falling, the frictional torque is in the opposite direction from the gravitational torque. However, when the same mass is rising, the frictional and the gravitational torques are acting in the same direction.

Equations of Motion

When the mass is falling, the equation for rotational motion is

( 2 )

Στ = RT_f − τ_F = Iα_f,

and when the mass is rising

( 3 )

Στ = RT_r + τ_F = Iα_r.

Here, T_f and T_r are the tensions when the mass is falling and rising respectively, τ_F is the torque due to friction, α_f and α_r are the angular accelerations when the mass is falling and rising respectively, and R is the radius of the pulley. The tension can be found from an application of Newton's Second Law to this system. In both cases, the tension is T = M(g – αR). The equations 1, 2, and 3 can be solved to give

( 4 )

I =

MgR

− MR² ≈

MgR

Thus, if we use the average of the falling and rising α values, the effect of friction will be eliminated. Neglecting the term MR² introduces a small (~1%) error, and for simplicity we will ignore it here.

Energy

When the mass begins to fall, the gravitational potential energy will transfer to the kinetic energy.

Potential Energy

The change in potential energy can be found using the equation:

( 5 )

ΔPE = PE_f − PE_i,

where PE_i is the initial gravitational potential energy in the system and PE_f is the final gravitational potential energy in the system. These are defined as the following.

( 6 )

PE_i = Mgh_i

( 7 )

PE_f = Mgh_f

Equations 5, 6, and 7 can be solved to give:

( 8 )

ΔPE = Mg(h_f − h_i).

Kinetic Energy

The change in kinetic energy can be found using the equation:

( 9 )

ΔKE = KE_f − KE_i,

where KE_i is the initial kinetic energy in the system, and KE_f is the final kinetic energy in the system. KE_i and KE_f are defined for rotational motion as the following.

( 10 )

KE_i =

Iω_i²

( 11 )

KE_f =

Iω_f²

Plugging the equations 10 and 11 into 9, we will get:

( 12 )

ΔKE =

Iω_f²

−

Iω_i²

Conservation of Energy

The total mechanical energy is conserved in the frictionless system, which means the following.

( 13 )

−ΔPE = ΔKE

( 14 )

−Mg(h_f − h_i) =

Iω²_f

−

Iω²_i

The negative sign indicates that the potential energy decreases as kinetic energy increases, which means the total mechanical energy is conserved. We did not include the elastic potential energy because we can neglect the stretch in the string in our experiment. You have to check the Law of Conservation of Mechanical Energy using experimental data from one of the runs.

Procedure

Please print the worksheet for this lab. You will need this sheet to record your data.

Calculate the theoretical value for the moment of inertia for the disk.

Open the pre-set experiment file: labs/PreSetupfiles/PHY113.

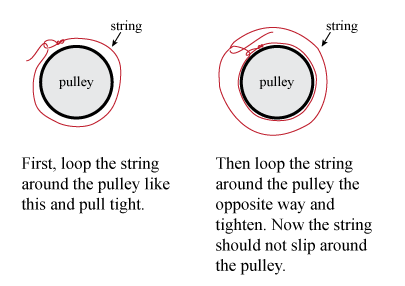
Figure 3: Attaching the string correctly.

Record the angular velocity vs. time data for the following cases.

A
string wound around the medium pulley, M = 50 g
B
string wound around the medium pulley, M = 70 g
C
string wound around the large pulley, M = 50 g
D
string wound around the large pulley, M = 70 g
E
string wound around the large pulley, M = 100 g

To find the angular acceleration α for a certain part of the motion, select the corresponding segment of the data on the graph and apply the linear fit to it. In each case, to calculate the experimental value of the moment of inertia, remember to use the averaged angular acceleration α from 4 (or more, but an even number) sections of the plot.

For one of the runs, determine if the energy is conserved by comparing the maximum change in potential energy with the maximum change in kinetic energy.

A
Measure the distance that mass M falls from the starting point (kinetic energy is zero and the potential energy is maximum) to the bottom of the fall (kinetic energy is maximum while the potential energy is minimum) with the metric ruler provided. Use masking tape to mark initial and final position.
B
To collect the data of the maximum angular velocity, use the "Smart tool" feature or "Statistics" in the angular velocity vs. time graph.

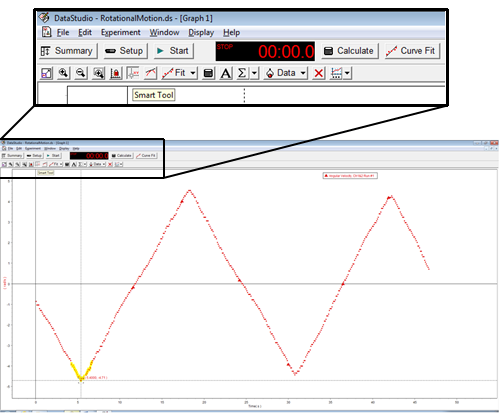
Figure 4a: How to measure the maximum velocity - Smart Tool.

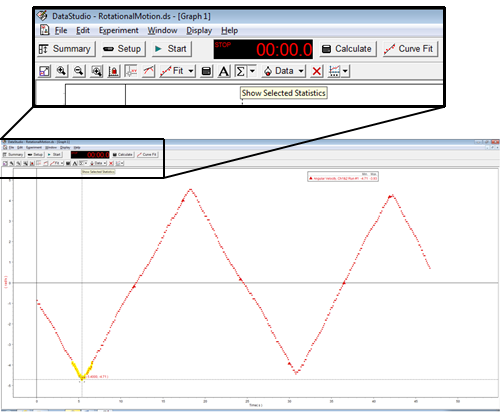
Figure 4b: How to measure the maximum velocity - Statistics.

Discussion

Start your discussion with the statement of the purpose of the lab experiment, then provide a brief theoretical explanation about expected results. Discuss if the graphs generated in class show the expected relationship between the physics quantities (angular velocity and time). Report your best experimental results. How do the theoretical and empirical values of the moment of inertia of the disk compare? What is the percent discrepancy (difference) between the theoretical and experimental results? Are the results accurate and/or consistent? (In general, the experimental results are considered accurate if the percent discrepancy/difference is within 10-15% depending on the experimental setup used to prove the theoretical concept.) What have you proven/learned about moment of inertia? What are the reasons for random and/or systematic errors? How can they be reduced in the experiment? The following questions need to be a part of your discussion section. Was energy conserved in this experiment? If some percent of mechanical energy has been lost, where did it get transferred to?

Conclusion

Provide a clear statement as to whether or not the objective of the Lab "Rotational motion" is met. Do your experimental results confirm the validity of Newton's Second Law for rotation motion? Support all your answers with evidence.