Basic Concepts of Error Analysis
Significant Figures
The laboratory usually involves measurements of several physical quantities such as length, mass, time, voltage and current. The values of these quantities should be presented in terms of Significant Figures.
For example, the location of the arrow is to be determined in the figure below.

It is obvious that the location is between 1 cm and 2 cm. The correct way to express this location is to make one more estimate based on your intuition. That is, in this case, a reading of 1.3 cm is estimated. This measurement is said to contain two significant figures. Note that there should only be one estimated place in any measurement. If data are to contain, say, three significant figures, two must be known, and the third estimated. Do not try to locate the position of the arrow in fig. 1 as 1.351 cm.

It is obvious that the location is between 1 cm and 2 cm. The correct way to express this location is to make one more estimate based on your intuition. That is, in this case, a reading of 1.3 cm is estimated. This measurement is said to contain two significant figures. Note that there should only be one estimated place in any measurement. If data are to contain, say, three significant figures, two must be known, and the third estimated. Do not try to locate the position of the arrow in fig. 1 as 1.351 cm.
-
aSpecify the measured value to the same accuracy as the error. For example, we report that a physical quantity isx = 3.45 ± 0.05,not3.4 ± 0.05and not3.452 ± 0.05.
-
bWhen adding or subtracting numbers, the answer is only good to the least accurate number present. For example,50.3 + 2.555 = 53.9and not 52.855.
-
cWhen multiplying or dividing, keep the same number of significant figures as the factor with the fewest number of significant figures. For example,5.0 · 1.2345 = 6.2and not 6.1725.
Types of Errors
Every measurement has its error. In general, there are three types of errors that will be explained below.Random Errors
This type of error is usually referred to as a statistical error. This class of error is produced by unpredictable or unknown variations in the measuring process. It always exists even though one does the experiment as carefully as is humanly possible. One example of these uncontrollable variations is an observer's inability to estimate the last significant digit for a given measurement the same way every time.Systematic Errors
This class of error is commonly caused by a flaw in the experimental apparatus. They tend to produce values either consistently above the true value, or consistently below the true value. One example of such a flaw is a bad calibration in the instrumentation.Personal Errors
This class of error is also called "mistakes." It is fundamentally different from either the systematic or random errors stated above, and can be completely eliminated if the experimenter is careful enough. One example of this type of error is to misread the scale of an instrument.Mean and Statistical Deviation
Let's assume that both the systematic and personal errors can be eliminated by careful experimental procedures, then we can conclude that the experimental errors are governed by random statistical errors. If there are a total number of N measurements made of some physical quantity, say, x, and the i-th value is denoted by xi, the statistical theory says that the "mean" of the above N measurements is the best approximation to the true value; i.e., the meanx
is given by
( 1 )
x =
(x1 + x2 + x3 + − − − + xN),
 |
| 1 |
| N |
 |
| N | |
 | |
| i=1 |
 |
| 1 |
| N |
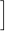 |
( 2 )
σ =
=
.
 |
|
 |
|
Reporting of Results
Typically, in the laboratory, one will be asked to make a number of repeated measurements on a given physical quantity, say x. The measured value is customarily expressed in the laboratory report as( 3 )
x = x ± σ,
x
is the mean and σ is the standard deviation. Equivalently, we can also write
( 4 )
x = x
· 100%
,
 |
| σ |
| x |
 |
 |
| σ |
| x |
 |
Propagation of Errors
In carrying out an experiment, a specific physical quantity of interest is usually obtained by an indirect measurement and a simple manipulation of other physical quantities. For instance, in the laboratory, speed is determined indirectly by the division of the distance traveled and the time taken to travel that distance. It is clear from our previous discussion that these measurements of distance and time inevitably have errors associated with them. In evaluating the speed, these errors on distance and time will pass on to the speed. Consider two independent physical quantities x and y with their associated errors Δx and Δy, respectively. We are interested in knowing how the errors propagate to another physical quantity z formed under the following specific operations.Addition
( 5 )
z = x + y
( 6 )
Δz = Δx + Δy.
(3.0 ± 0.1) + (4.0 ± 0.2) = 7.0 ± 0.3.
Subtraction
( 7 )
z = x − y
( 8 )
Δz = |Δx| + |−Δy|
( 9 )
Δz = Δx + Δy.
(5.0 ± 0.1) − (1.0 ± 0.3) = 4.0 ± 0.4.
Multiplication
( 10 )
z = x · y
( 11 )
Δz = Δx · y + x · Δy
( 12 )
| Δz |
| z |
| Δx |
| x |
| Δy |
| y |
(1.0 ± 0.1) · (3.0 ± 0.3) = (1.0 ± 10%) · (3.0 ± 10%) = 3.0 ± 20% = 3.0 ± 0.6.
Division
( 13 )
z =
| x |
| y |
( 14 )
Δz =
+
x ·
,
 |
| Δx |
| y |
 |
 |
| −Δy |
| y2 |
 |
( 15 )
| Δz |
| z |
| Δx |
| x |
| Δy |
| y |
| (3.0 ± 0.3) |
| (1.0 ± 0.1) |
| (3.0 ± 10%) |
| (1.0 ± 10%) |
Powers or Exponential
( 16 )
z = xk
( 17 )
Δz = k · xk−1 · Δx
( 18 )
| Δz |
| z |
| Δx |
| x |
(3.0 ± 0.3)2 = (3.0 ± 10%)2 = 9.0 ± 2 · 10% = 9.0 ± 20% = 9.0 ± 1.8.
