The Mean and Median
The mean of a numerical data set is just the familiar arithmetic average: the sum of the observations divided by the number of observations. The median strip of a highway divides the highway in half, and the median of a numerical data set does the same thing for a data set. Once the data values have been listed in order from smallest to largest, the median is the middle value in the list, and it divides the list into two equal parts.
Comparing the Mean and the Median
The median is the value on the measurement axis that separates the smoothed histogram into two parts, with half (50%) of the area under each part of the curve. The mean is a bit harder to visualize. If the histogram were balanced on a triangle (a fulcrum), it would tilt unless the triangle was positioned at the mean. The mean is the balance point for the distribution.
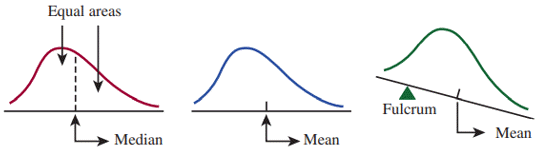
Three identical curves above three different horizontal axes are shown. All three curves start just above the horizontal axis, go up and right at a steep angle, reach a peak close to the left side of the horizontal axis, go down and right at a gentle angle, and end just above the horizontal axis.
- For the first curve, a point on the horizontal axis just to the right of the peak is labeled "Median." The areas under the curve to the left and right of this point are labeled "Equal areas."
- For the second curve, a point on the horizontal axis just to the right of the peak is labeled "Mean."
- The third curve's axis is drawn tilting down and to the right with the curve tilting along with it. A triangle labeled "Fulcrum" is positioned under the horizontal axis just to the left of the peak such that the top point of the triangle touches the axis. A point on the horizontal axis just to the right of the peak is labeled "Mean."
When the histogram is symmetric, the point of symmetry is both the dividing point for equal areas and the balance point, and the mean and the median are equal. However, when the histogram is unimodal (single-peaked) with a longer upper tail (positively skewed), the outlying values in the upper tail pull the mean up, so it generally lies above the median. For example, an unusually high exam score raises the mean but does not affect the median. Similarly, when a unimodal histogram is negatively skewed, the mean is generally smaller than the median
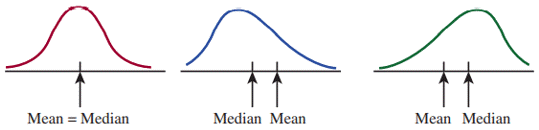
Three curves above three different horizontal axes are shown.
- The first curve is symmetrical and starts just above the horizontal axis, goes up and right, reaches a peak, goes down and right, and ends just above the horizontal axis. The point on the horizontal axis below the peak is labeled "Mean = Median."
- The second curve starts just above the horizontal axis, goes up and right at a steep angle, reaches a peak close to the left side of the horizontal axis, goes down and right at a gentle angle, and ends just above the horizontal axis. A point on the horizontal axis just to the right of the peak is labeled "Median" and a point a bit further to the right is labeled "Mean."
- The third curve starts just above the horizontal axis, goes up and right at a gentle angle, reaches a peak close to the right side of the horizontal axis, goes down and right at a steep angle, and ends just above the horizontal axis. A point on the horizontal axis just to the left of the peak is labeled "Median" and a point a bit further to the left is labeled "Mean."