Print

Lab 7 - Determination of the Molar Mass of an Unknown Solid by Freezing Point Depression

Goal and Overview

In the first part of the lab, a series of solutions will be made in order to determine the freezing point depression constant, Kf, for cyclohexane. The freezing points of these solutions, which will contain known amounts of p-dichlorobenzene dissolved in cyclohexane, will be measured. In the second part of the lab, the freezing point of a cyclohexane solution will be prepared that contains a known mass of an unknown organic solid. The measured freezing point change will be used to calculate the molar mass of the unknown solid.

Objectives and Science Skills

Suggested Review and External Reading

Background

If a liquid is at a higher temperature than its surroundings, the liquid's temperature will fall as it gives up heat to the surroundings. When the liquid's temperature reaches its freezing point, the liquid's temperature will not fall as it continues to give up heat to the surroundings. Instead, the liquid will begin to freeze. Those parts closest to the cold surroundings will turn from liquid to solid. This freezing process releases a quantity of heat energy that is equal in magnitude but opposite in sign to the heat of fusion, ΔHfusion, of the substance. ΔHfusion is defined as the heat absorbed by a solid in the process of melting. When the liquid freezes to form the solid phase, it must give up the same amount of heat: ΔHfreezing = – ΔHfusion. The temperature of the system (the freezing liquid) remains at the freezing point until all of the liquid has frozen. If you plot temperature against time for this process, the curve will resemble that shown. Once the liquid has completely frozen, only then will the temperature start to fall again.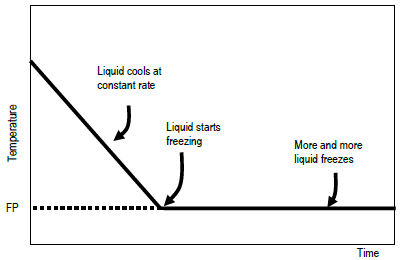
Figure 1

Figure 1: Idealized plot of temperature vs. time to determine freezing

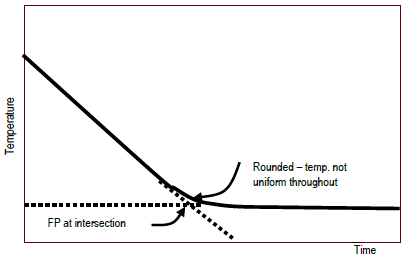
Figure 2

Figure 2: Typical experimental plot of temperature vs. time to determine point

Typical idealized and experimental plots are shown. The temperature curve on the experimental plot is rounded, rather than sharp. The system has warmer and colder regions even though it is being stirred, but the thermometer can only measure an average temperature. To extract a unique freezing point from the rounded corner on the plot, straight lines are drawn that extend the steeply falling part and the nearly horizontal part of the curve. The experimental freezing point is the temperature at which these two lines intersect. This is shown in Figure 2. The freezing point of a liquid and the melting point of a solid occur at the same temperature. This temperature is defined as the point at which the solid and liquid phases coexist in equilibrium with each other under a given pressure. This is shown in Figure 3.
Figure 3

Figure 3

( 1 )
Tf° (≡ Tm°) when Ratel°→s° = Rates°→l°
 
The fact that these two phases are in equilibrium does not mean that molecules are not passing from one phase to the other. The equilibrium is dynamic. Molecules are constantly passing from one phase into the other but the rates of these processes are equal. At equilibrium, the number of molecules leaving and entering the solid phase per unit time are equal. Suppose a solute is dissolved into the liquid. The solute will not enter the solid phase because the incorporation of solute molecules into the crystal structure of the solid solvent is usually energetically unfavorable. This keeps impurities (the solute) out of the solid phase as the liquid freezes. The solute remains in the liquid phase only. A molecular view is helpful in understanding what is observed experimentally. To do this, we need to define entropy. Entropy is a measure of the disorder of a system. Higher entropy is more disordered (e.g., a liquid); lower entropy is less disordered (e.g., a solid). Phase changes involve changes in both energy and in entropy. At the freezing point, the kinetic energy of the particles becomes low enough for inter-particle forces to lock the particles into fixed positions in the solid crystal structure. However, if solute particles are present, the entropy of the liquid phase is increased. To reach the freezing point of the solution, the temperature has to be lower than it is in the case of the pure solvent. The system must reach the point where the energy and entropy are low enough for the inter-particle forces to take control and fix the sovent particles in position in the crystal structure. Therefore, the temperature at which the solution freezes is lower than that of the pure solvent. The change in the freezing point is proportional to the amount of solute added. This phenomenon is called freezing point depression. Another way to think about freezing point depression is to consider the solid surface area available to the solvent molecules. Solute particles are present at the liquid-solid interface, effectively decreasing the surface area of the solid accessible to the solvent molecules. This decreases the rate at which liquid-phase solvent molecules can stick to the solid. The solute molecules do nothing to the rate at which sufficiently energetic molecules leave the solid phase. The rate of freezing is slowed while the rate of melting is unchanged. As the temperature is lowered, the rate of freezing (sticking) is increased, and the rate of melting is decreased. At some temperature below the freezing point of the pure solvent, the rates of freezing and melting will be equal (freezing point depression).
Figure 4

Figure 4

The change in the freezing point is defined as:
ΔTf = Tf,solution − Tf,solvent.    ΔTf
 is negative because the temperature of the solution is lower than that of the pure solvent. Freezing point depression is one of four important colligative properties of ideal solutions (freezing point depression, boiling point elevation, vapor pressure decrease, and osmotic pressure increase) in which the change in the solvent properties is dependent on the concentration, not the identity, of the solute particles. When determining changes in freezing point (or boiling point), solute concentration is usually not measured in molarity (moles of solute per liter of solution), but, rather, in molality. Molality is moles of solute per kilogram of solvent. The concentration unit mol/kg is temperature independent, unlike the mol/L concentration unit, because volume changes with temperature but mass does not.
( 2 )
molality ≡
moles of solute
mass of solvent in kilograms
 ≡
nsolute
msolvent (kg)
 = [solute] 
The magnitude of the freezing point change is proportional to the molality of the dissolved solute:
ΔTf∝
 [solute]. The proportionality constant, Kf , is called the molal freezing point constant. It is specific to a particular solvent. Thus, the following equation.
( 3 )
ΔTf,solution − ΔTf,solvent = ΔTf = −Kf [solute] = −Kf
nsolute
msolvent (kg)
 
The minus sign in the last two expressions in Eq. 3
ΔTf,solution − ΔTf,solvent = ΔTf = −Kf [solute] = −Kf
nsolute
msolvent (kg)
 
 result in a positive Kf because ΔT is negative while concentration is positive. In some texts, Kf is given as a negative value. If this is the case, the – sign in Eq. 3
ΔTf,solution − ΔTf,solvent = ΔTf = −Kf [solute] = −Kf
nsolute
msolvent (kg)
 
 is not used. Just keep in mind that the freezing point of the solution is lower than that of the pure solvent. For most solutions, the value of Kf depends on the solvent, not on the solute. Once you have measured Kf for a solvent with one solute, you can use Eq. 3
ΔTf,solution − ΔTf,solvent = ΔTf = −Kf [solute] = −Kf
nsolute
msolvent (kg)
 
 and the same value of Kf for other solutes. Freezing point depression provides a convenient way to determine the molar mass of an unknown substance. A solution containing a known mass of solute per mass of solvent is prepared and its freezing point is measured. The number of moles of solute can be determined by rearranging Eq. 3
ΔTf,solution − ΔTf,solvent = ΔTf = −Kf [solute] = −Kf
nsolute
msolvent (kg)
 
 to solve for moles of solute, nsolute:
( 4 )
ΔTf = −Kf
nsolute
msolvent (kg)
 ⇒ nsolute =
ΔTf · msolvent (kg)
−Kf
 
Because the mass of unknown solute is known (measured on the balance) and the number of moles has been calculated (by Eq. 4
ΔTf = −Kf
nsolute
msolvent (kg)
 ⇒ nsolute =
ΔTf · msolvent (kg)
−Kf
 
), you can determine the molar mass of the unknown solute using the equation below.
( 5 )
MMsolute =
msolute
nsolute
 
You will be working with cyclohexane as your solvent.
formula = C6H12
MM = 84.160 g/mol
ρ = 0.779 g/mL at 20°C
Tf = 6.5°C
Kf = 20.2°C/mol/kg

Procedure

Caution:
Cyclohexane is highly flammable. No flames are permitted in the lab.
Caution:
para-Dichlorobenzene and the organic unknowns are irritants and should not be inhaled or allowed to touch the skin.
Caution:
Dispose of all solutions as instructed. Nothing may go down the sink.
Caution:
Wear your goggles at all times, including trips to the stockroom.
Caution:
Be careful with the thermometer. Report a mercury spill: it must be cleaned up immediately.
To minimize reagent contamination, never put anything into a reagent bottle. Never pipet out of a reagent bottle. Transfer some liquid into a beaker and pipet out of that. Please use the pipets that are out on the reagent bench. Do not wash them with water. Please return them when you are done. The freezing point apparatus is shown in figure 5.
Figure 5

Figure 5: Freezing-Point Apparatus

1
Carefully adjust the height of the thermometer so the entire mercury bulb is immersed in the liquid but so that there is room for the stir bar beneath it.
2
Carefully rotate the split stopper so the graduations on the thermometer are visible through the split. Make sure the utility clamp is located so that you can easily read the thermometer.
3
Prepare an ice-water slurry. Fill your 250-mL beaker with ice, add enough water to fill the spaces, and stir. The temperature should be within a degree or two of 0°C.
4
Clean your test tubes and dry thoroughly. The tube must be completely dry before cyclohexane is added. Rinse the clean test tubes with 1-2 mL cyclohexane to remove impurities; dispose rinse liquid properly in the hood. Dry the test tube.
The liquid waste bottle in the fume hood is for small cyclohexane rinse volumes only, NOT USED SOLUTION.

Part 1: Determination of Kf for Cyclohexane

The freezing point must be within the temperature range spanned by your solutions of known solute molality. It is also important that part 2 is done well. Do part 2 first and repeat it again last.

A. Pure cyclohexane:

1
Weigh the first empty tube, stir bar included, to 0.01 g (pan balance). It may be easier to put the test tube in a beaker to take the mass.
2
Pipet in 20 mL of cyclohexane and reweigh to 0.01 g.
3
Stopper the test tube with the split stopper and adjust the apparatus so that 1) the thermometer does not touch the side of the test tube, and 2) all of the solution in the tube is immersed below the surface of the ice bath.
4
Work with a partner to record the time and temperature data. Practice doing this quickly and accurately. Start timing when the temperature gets just above 13°C. Record the temperature to the tenths place as accurately as possible every five seconds. Be prepared to read and record quickly.
5
Eventually, the change in temperature will slow enough that readings can be taken every 10 seconds. When the liquid starts to freeze, the temperature change will be very small. Take several data points after this happens (temperature readings are roughly constant). You should have two significant figures in your freezing point temperature.
6
If you need to repeat a trial to get better data, warm the test tube and then put it back into the ice bath. Repeat the experiment enough times so that your data are accurate and reproducible.

B. para-Dichlorobenzene solutions of known concentrations:

Stop. Please check with your TA if you are to do this section. If you are instructed to go to part 2, please use the literature value of Kf for cyclohexane (20.2°C/molal).
1
Precisely weigh enough p-dichlorobenzene to make a roughly 0.05 molal solution when added to your 20 mL of cyclohexane.
2
Weigh the solid on the analytical balance. Make sure that all of the solid is transferred into the test tube and that it completely dissolves before making any temperature measurements. Do not weigh out the p-dichlorobenzene in advance of using it because it is a volatile solid (it sublimes quite rapidly).
3
Once your solution is prepared, take time-temperature data.
4
Accurately weigh enough p-dichlorobenzene to make a roughly 0.10 molal solution when added to the solution you already have in your test tube. Dissolve the additional solid in your solution and take time-temperature data.
5
Prepare and take time-temperature data for an approximately 0.15 molal solution.
6
Determine the freezing point of the pure solvent and of each solution of known molality: Make freezing point (time-temperature) plots — ask your TA for the number of plots required.
  • a
    Plot temperature against time for all solutions.
  • b
    From the graphs, find the freezing point (as described in the Background section).
  • c
    Also determine an uncertainty in freezing point for each solution.
7
Determine the molal freezing point depression constant, Kf:
  • a
    Calculate actual molalities of the p-dichlorobenzene solutions using the mass measurements and the molar mass of the solute.
  • b
    Plot
    −ΔTf
     against molality (
    −ΔTf
     is a positive quantity because
    ΔTf
     is negative) for your four data points (concentrations of 0, ~0.5, ~0.10, and ~0.15 mol/kg).
  • c
    Fit the best straight line to your four points and determine the equation for the line with the proper units.
  • e
    Compare your value with the literature value of 20.2°C/mol/kg.
When you are done: Stopper your test tubes. Label them with the contents, your name, and your section. Immediately turn them in to the stockroom for disposal. Improper disposal of your organic waste solutions will result in your immediate ejection from the lab and from the course.

Part 2: Molar Mass of an Unknown Organic Solid (para-dihalobenzene)

1
Weigh the second clean, dry test tube with a stir bar to 0.01 g.
2
Pipet in 20 mL cyclohexane and reweigh. Do another determination of the freezing point of the pure solvent before adding the unknown solute (i.e., take time-temperature measurements for this sample of pure solvent).
3
To determine the freezing point of a solution with a known mass of unknown solute, accurately weigh about 0.37 g of your unknown organic solid on the analytical balance (to 0.0001 g). This mass will produce a sufficient freezing point change while minimizing waste.
4
Completely dissolve the unknown solid in the cyclohexane. Take time-temperature data and find the new freezing point of the solution to two significant figures.
5
Use Kf (to three significant figures) and your freezing point change (to two significant figures) to calculate the number of moles and then the molar mass of your unknown solid (two significant figures).
6
The unknown is a para-dihalobenzene (halo = fluoro, chloro, bromo, or iodo). Report the identity of your unknown based on the molar mass.
When you are done: Stopper your test tube. Label it with the contents, your name, and your section. Immediately turn it in to the stockroom for disposal. Improper disposal of your organic waste solutions will result in your immediate ejection from the lab and from the course.

Reporting Results

Complete your lab summary or write a report (as instructed).

Results

Sample Calculations:

Discussion/Conclusions

Review

Copyright © 2011 Advanced Instructional Systems, Inc. and the University of California, Santa Cruz | Credits