WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Tuesday, April 1, 2025 04:52 EDT

Home My Assignments Grades Communication Calendar My eBooks

Serway and Faughn - College Physics 7/e (Homework)

James Finch

Physics - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 17 / 24

Due : Monday, January 28, 2030 00:00 EST

Last Saved : n/a Saving...  ()

Print Assignment
Question
Points
1 2 3 4 5 6 7
3/3 1/1 –/4 –/1 7/7 4/6 2/2
Total
17/24 (70.8%)

  • Instructions

    College Physics by Serway and Faughn now has animations with conceptual questions and tutorial problems offering feedback and hints to guide student content mastery, as well as over 1600 end-of-chapter questions.

    Students will see a detailed solution, in blue, using the algorithmically-generated values in the question, at the instructor's discretion--for example, after a particular submission or after the assignment due date has passed.

    You can check out a sampling of this exciting development below. WebAssign is the most utilized homework system in physics. Designed by physicists for physicists, WebAssign, easy to use, reliable--a trusted companion to your teaching. Sign up for a Test Drive today!

    Question 1 is a traditional end-of-chapter question, with conditional feedback for incorrect numerical answers. (For this demo, the solution is displayed immediately after the question has been submitted using the algorithmically-generated values.)

    Question 2 is an end-of-chapter question enhanced by adding a link to an Active Figure. The solution is displayed after the question has been answered.

    Question 3 and 4 show Active Figure questions which have been imported into WebAssign.

    Question 5 is a new Active Example which helps guide students through the process needed to master a concept.

    Question 6 is a Quick Quiz question with customized feedback added to the numerical portion.

    Question 7 is a Math Review question from the math review appendix.

    Click here for a list of all of the questions coded in WebAssign. This demo assignment allows many submissions and allows you to try another version of the same question for practice.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 3/3 points  |  Previous Answers SerCP7 4.P.015.soln. My Notes
Question Part
Points
Submissions Used
1 2 3
1/1 1/1 1/1
4/50 3/50 5/50
Total
3/3
 
Find the tension in each cable supporting the 660 N cat burglar in Figure P4.15. Assume the angle of the inclined cable is 38.0°.
inclined cable Correct: Your answer is correct. N
horizontal cable Correct: Your answer is correct. N
vertical cable Correct: Your answer is correct. N


Figure P4.15

A traditional end-of-chapter question, with conditional feedback for incorrect numerical answers. (For this demo, the solution is displayed immediately after the question has been submitted using the algorithmically-generated values.)



Note from WebAssign: All numerical end-of-chapter questions will give feedback to the student when an incorrect answer is submitted. Please see the algorithmically generated solution below.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
2. 1/1 points  |  Previous Answers SerCP7 5.P.044.AF. My Notes
Question Part
Points
Submissions Used
1
1/1
1/50
Total
1/1
 
A child slides without friction from a height h along a curved water slide (Fig. P5.44). She is launched from a height h/5 into the pool. Determine her maximum airborne height y in terms of h and . (Use theta for and h as appropriate.)
Click here to preview your answer.
Click here for help with symbolic formatting.


Figure P5.44

Refer to the Active Figure Simulation to review the concepts this question addresses. Hint: Active Figure 5.15



Note from WebAssign: The answer is any expression mathematically equal to
h/5 * (4*(sin(theta))^2 + 1)
Please see algorithmically generated solution below.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
3. –/4 points SerCP7 4.AF.21. My Notes
Question Part
Points
Submissions Used
1 2 3 4
–/1 –/1 –/1 –/1
0/50 0/50 0/50 0/50
Total
–/4
 
Active Figure 4.21 Acceleration Up and Down an Incline with Friction

The external forces exerted on a block lying on a rough incline are the gravitational force mg, the normal force n, and the force of friction f. For convenience, the gravitational force is here is resolved into a component along the incline and a component perpendicular to the incline.

Instructions: Turn friction on or off using the drag button and click start to project the block up the incline. You can use the back, pause and fwd buttons to stop the block's motion at any point and step through one frame at a time.

Exploration 1

For this Exploration, set the drag button to off. Reset the the block and start a sequence. Observe how the block rises to a highest point and then moves down the slope out of view. Reset the block and start another sequence, but this time use the pause, back and fwd button to freeze the block at its highest point. Record the time, distance and acceleration at this highest point. The acceleration graph in the upper right-hand corner of the screen shows that the acceleration is constant throughout the entire motion sequence. Why?

(a) From your results recorded above, find the following quantities.
The angle of the incline -- measured with respect to the horizontal.
°
Hint


From the block's given initial speed of 6.8 m/s up the incline, use the kinematic equation v2 = v20 + 2ax to calculate the distance traveled up the incline. Does your calculated value equal the value recorded above?

Use another kinematic equation to calculate the time to reach the highest point. Does this value agree with the value recorded above?

Exploration 2

Click the drag button to introduce a kinetic frictional force on the block. Reset the block and run a full sequence. Notice in this case that the acceleration varies from a maximum value of 8.61 m/s2 to a minimum value of 1.19 m/s2.

To understand why the acceleration now changes, play the animation a few times, paying close attention to the free-body diagram. Use the pause button to play a few frames right around the highest point. Recall that friction always acts opposite to the direction of slide. So, while the block slides up the incline, the friction points down the incline -- and vice-versa.

To find the magnitude of the friction force, apply Newton's second law in a direction perpendicular to the incline.
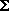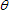
Fy = -mg cos = 0

fk = µkn = µkmg cos
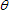
While the block is sliding up the incline (negative direction), Newton's second law applied in a direction parallel to the incline gives the following.
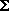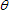
Fx = sin() + fk = maup
However, when the block slides down the incline, Newton's second law becomes:
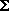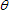
Fx = mg sin - fk = madown
(b) Use either of the last two equations to solve for the coefficient of kinetic friction. Double-check with the other equation.
µk =
Hint



Exercise 4.AF.21

Suppose that the coefficient of kinetic friction in the above animation is decreased to 0.267. Calculate the magnitude of acceleration up and down the incline.
(c) Acceleration up the incline
aup = m/s2
(d) Acceleration down the incline
adown = m/s2
Hint
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
4. –/1 points SerCP7 12.AF.02. My Notes
Question Part
Points
Submissions Used
1
–/1
0/50
Total
–/1
 
Active Figure 12.2: Work Done on a Gas for Different PV Processes

In this animation, you can choose one of the three process simulations and see the simulation evolve in the corresponding PV diagram. Readouts are provided for the thermodynamic state variables P, V and T, and for the work done on the gas during the simulation. The area under the PV curve is shaded.

Instructions: Click one of the three sim buttons to see the process simulated by the piston and diagrammed in the PV graph.
Explore

Play each simulation, and pay attention to how the state variables change in each case. Compare the value indicated in the work readout to the shaded area under each PV-curve.

When you are ready, match the item on the left with the most appropriate item on the right. Do not match items that are identical in both columns.

Hint
isothermal
simulation 2
simulation 1
isovolumetric followed by isobaric
isobaric followed by isovolumetric


Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
5. 7/7 points  |  Previous Answers SerCP7 4.AE.01. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5
0/0 0/0 5/5 1/1 1/1
1/50 1/50 4/50 4/50 1/50
Total
7/7
 
Example 4.1 Airboat
Goal Apply Newton's law in one dimension, together with the equations of kinematics.

Problem An airboat with mass 4.46 102 kg, including passengers, has an engine that produces a net horizontal force of 8.26 102 N, after accounting for forces of resistance.

(a) Find the acceleration of the airboat.

(b) Starting from rest, how long does it take the airboat to reach a speed of 15.8 m/s?

(c) After reaching this speed, the pilot turns off the engine and drifts to a stop over a distance of 50.0 meters. Find the resistance force, assuming it's constant.
Figure 4.4 from book
Figure 4.4
Strategy In part (a), apply Newton's 2nd law to find the acceleration, and in part (b) use this acceleration in the one-dimensional kinematics equation for the velocity. When the engine is turned off in part (c), only the resistance forces act on the boat, so their net acceleration can be found from v2 - v02 = 2ax. Then Newton's second law gives the resistance force.

Solution
(a) Find the acceleration of the airboat.
Apply Newton's 2nd law to solve for the acceleration. ma = Fnet a = F_(net)/ m = (8.26 text( x ) 10^2 text( N))/( 4.46 text( x ) 10^2 text( kg))
a = Correct: Your answer is correct. m/s2
(b) Find the time necessary to reach a speed of 15.8 m/s.
Apply the kinematics velocity equation: v = at + v0 = 15.8 m/s
t = Correct: Your answer is correct. s
(c) Find the resistance force after the engine is
turned off.
Using kinematics, find the net acceleration due to resistance forces. v2 - v02 = 2ax
0 - (15.8 m/s)2 = 2a(50.0 m)
a = Correct: Your answer is correct. m/s2
Substitute the acceleration into Newton's second law, find the resistance force. Fresist = ma = (4.46 102 kg)a
Fresist = Correct: Your answer is correct. N
Hint


Remarks The negative answer for the acceleration in part (c) means that the airboat is slowing down. In this problem, the components of the vectors and were used, so they were written in italics without being bolded. It's important to bear in mind that and are vectors, not scalars.
Decorative only

Decorative only
Exercise 4.1 Hints: Getting Started | I'm Stuck
Decorative only
Suppose the pilot, starting again from rest, opens the throttle only partway. At a constant acceleration, the airboat then covers a distance of 64.4 meters in 11.7 seconds. Find the net force acting on the boat.
F = Correct: Your answer is correct. N
Decorative only
Decorative only

Note from WebAssign
If a student makes one of several common mistakes on the Exercise portion above, they will get feedback specific to the mistake they made. If their answer is incorrect but does not meet one of these specific conditions, they will still get generic numerical feedback as to how far off they are, or if they appear to have made just a sign or order of magnitude error, etc.

Try some of these values to see what feedback you get!
Incorrect formulaIncorrect answer
md/t2 210.
(2md/t)2 2.41e+07
20md/t2 4.20e+03
md/(2t2) 105
Correct formula Correct answer
2md/t2 420.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
6. 4/6 points  |  Previous Answers sercp7 12.qq.03.nva My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6
1/1 1/1 1/1 1/1 –/1 –/1
2/50 1/50 2/50 3/50 0/50 0/50
Total
4/6
 
Three engines operate between reservoirs separated in temperature by 300 K. The reservoir temperatures are as given below.
  Th (K)Tc (K)
Engine A1,000700
Engine B800500
Engine C600300

Rank the engines in order of theoretically possible efficiency, from highest to lowest.
Correct: Your answer is correct. > Correct: Your answer is correct. > Correct: Your answer is correct.

What is the efficiency of each engine?
Engine A Correct: Your answer is correct. %
Engine B %
Engine C %
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
7. 2/2 points  |  Previous Answers Math Review Question My Notes
Question Part
Points
Submissions Used
1 2
1/1 1/1
1/50 1/50
Total
2/2
 
Note from WebAssign: Each Serway textbook includes a Math Review Appendix. One such question is below. For an assignment of Math Review questions click here.

Quadratic Equations

Solve the following quadratic equation.
x2 + 5x - 6 = 0
x = Correct: Your answer is correct. (smaller value)
x = Correct: Your answer is correct. (larger value)

Refer to th.
Appendix A.3D
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
Home My Assignments
Enter a number.
Enter a number.
Enter a number.
Enter a mathematical expression.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.