WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Saturday, March 29, 2025 02:18 EDT

Home My Assignments Grades Communication Calendar My eBooks

My Cengage Home Notifications Help My Account

Math - College, section 1, Fall 2019
My Assignments

Zill - Differential Equations with Modeling 12/e (Homework)

James Finch

Math - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 15 / 51

Due : Sunday, January 27, 2030 00:00 EST

Last Saved : n/a Saving... ()

Ask Your Teacher Print Assignment

Question

Points

1	2	3	4	5	6	7	8	9
0/1	0/3	14/14	1/2	–/2	–/3	–/23	0/2	–/1

Total

15/51 (29.4%)

Instructions

A First Course in Differential Equations with Modeling Applications, 12th edition, by Dennis G. Zill, published by Cengage Learning, balances analytical, qualitative, and quantitative approaches to differential equation studies.

This demo assignment allows many submissions and allows you to try another version of the same question for practice wherever the problem has randomized values.

WebAssign provides a wide range of exercises that enable you to:

Build problem-solving skills (#1-3: Read Its, Watch Its, and (optional) Master Its)
Develop Conceptual Understanding (#4-7: Expanded Problems, modeling problems, and Project problems)
Address Readiness Gaps (#8-9: Power Series and Calculus Review)

The answer key and solutions will display after the first submission for demonstration purposes. Instructors can configure these to display after the due date or after a specified number of submissions.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 0/1 points | Previous Answers ZillDiffEQModAp12 2.2.004. My Notes

This exercise will build problem-solving skills.
Read It links are available as a learning tool under each question so students can quickly jump to the corresponding section of the eTextbook.

Solve the given differential equation by separation of variables.

dy − (y − 9)² dx = 0

y=−1x+9

Viewing Saved Work Revert to Last Response

2. 0/3 points | Previous Answers ZillDiffEQModAp12 2.3.008.MI. My Notes

This exercise will build problem-solving skills.
Students get just-in-time learning support with Watch It videos that contain narrated and closed-captioned videos walking students through the proper steps to solve a similar problem.
Master It tutorials are an optional student-help tool available within select questions for just-in-time support. Students can use the tutorial to guide them through the problem-solving process step-by-step using different numbers.

Find the general solution of the given differential equation.

y′ = 4y + x² + 7

y(x) =

c1y + x2 +c2

Give the largest interval I over which the general solution is defined. (Think about the implications of any singular points. Enter your answer using interval notation.)

Determine whether there are any transient terms in the general solution. (Enter the transient terms as a comma-separated list; if there are none, enter NONE.)

Need Help?

Viewing Saved Work Revert to Last Response

3. 14/14 points | Previous Answers ZillDiffEQModAp12 4.3.037.MI.SA. My Notes

This exercise will build problem-solving skills.
Master It tutorials—Standalone are embedded, step-by-step tutorials used to help students understand each step required to solve the problem, before inputting their final answer.

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Solve the given initial-value problem.

y′′′ + 12y′′ + 36y′ = 0, y(0) = 0, y′(0) = 1, y′′(0) = −5

Step 1

Recall the method for solving an nth-order homogenous differential equation by finding roots of an auxiliary equation.

a_ny⁽ⁿ⁾ + a_{n − 1}y^{(n − 1)} +

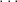
+ a₁y′ + a₀y = 0

Rewrite this as a polynomial in m, replacing the jth derivative with

m^j.

a_nmⁿ + a_{n − 1}m^{n − 1} +

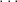
+ a₁m + a₀ = 0

Then for every root

m_i

of multiplicity k of this polynomial, the general solution for the equation must contain the following linear combination.

c₁e^m₁x + c₂xe^m₁x +

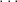
+ c_k x^{k − 1}e^m₁x

We are given the following third-order homogeneous differential equation.

y′′′ + 12y′′ + 36y′ = 0

Therefore, the auxiliary equation is a third-degree polynomial, which can be factored as follows.

m³ + 12m² + 36m

m(m² + 12m + 36)

m(m + 6)

m +

Solving for m, the roots of the auxiliary equation are

m₁ = 0

with multiplicity 1, and

m₂ = -6

-6

with multiplicity 2.

Step 2

From the root

m₁ = 0

with multiplicity 1, we know this means the general solution must contain

c₁e^(0)x = c₁.

From the root

m₂ = −6

with multiplicity 2, we know this means the general solution must contain

c₂e^−6x + c₃xe^−6x.

Therefore, the general solution of the differential equation contains the sum of these terms.

y = c₁ + c₂e^−6x + c₃

$$x·e−6x

$webMathematica generated answer key$

Step 3

We have found that the general solution of the equation is as follows.

y = c₁ + c₂e^−6x + c₃xe^−6x

We must solve the initial-value problem with given conditions. That is, solve for the constants c₁, c₂, and c₃.

First, find the first and second derivatives of y.

c₁ + c₂e^−6x + c₃xe^−6x

y′

−6c₂e^−6x + c₃e^−6x −

c₃xe^−6x

y′′

36c₂e^−6x − 6c₃e^−6x −

c₃e^−6x − 36c₃xe^−6x

36c₂e^−6x −

c₃e^−6x + 36c₃xe^−6x

Step 4

We have found the general solution y and its derivatives. Now we can substitute the given initial conditions.

Since

y(0) = 0,

we can state the following.

y	=	c₁ + c₂e^−6x + c₃xe^−6x
0 0	=	c₁ + c₂

Since

y′(0) = 1,

we can state the following.

y′

−6c₂e^−6x + c₃e^−6x − 6c₃xe^−6x

-6

c₂ + c₃

Since

y′′ (0) = −5,

we can state the following.

y′′

36c₂e^−6x − 12c₃e^−6x + 36c₃xe^−6x

−5

36c₂ −

c₃

Step 5

To solve for the constants in the general solution, we have three solutions in three unknowns.

c₁ + c₂	=	0
−6c₂ + c₃	=	1
36c₂ − 12c₃	=	−5

Solving for the constants results in the following.

c₁	=	7/36 7/36
c₂	=	-7/36 -7/36
c₃	=	-1/6 -1/6

Step 6

Recall the general solution of the differential equation is as below.

y = c₁ + c₂e^−6x + c₃xe^−6x

We also solved for the values of the constants given the initial conditions.

c₁

c₂

−

c₃

−

To finish, solve the given initial value problem.

y(x) =

$$736−736e−6x−16xe−6x

$webMathematica generated answer key$

You have now completed the Master It.

Need Help?

Viewing Saved Work Revert to Last Response

4. 1/2 points | Previous Answers ZillDiffEQModAp12 4.1.021.EP. My Notes

This exercise will develop conceptual understanding.
Expanded Problems enhance student understanding by going beyond a basic exercise and asking students to solve each step of the problem in addition to their final answer.

Consider the following functions.

f₁(x)	=	7 + x, f₂(x) = x, f₃(x) = x²
g(x)	=	c₁f₁(x) + c₂f₂(x) + c₃f₃(x)

Solve for

c₁, c₂,

and

c₃

so that

g(x) = 0

on the interval

(−∞, ∞).

If a nontrivial solution exists, state it. (If only the trivial solution exists, enter the trivial solution {0, 0, 0}.)

{c₁, c₂, c₃} =

Determine whether

f₁, f₂, and f₃

are linearly independent on the interval

(−∞, ∞).

linearly dependent linearly independent

Need Help?

Viewing Saved Work Revert to Last Response

5. –/2 points ZillDiffEQModAp12 3.3.007. My Notes

This exercise will develop conceptual understanding.
A wealth of exercises provide modelling problems on a variety of applications, building students' skills of putting their learnings to use.

Consider the two tanks A and B shown in the figure below.

Two cylindrical tanks are shown with 4 pipes connecting them in a system. The first tank is labeled A. The second tank is labeled B.
The first pipe connects the top of tank A to a point outside of the image, with an arrow pointing toward tank A that is labeled pure water 3 gal/min.

The second pipe connects tank A and B on the bottom of the tanks and has an arrow pointing from tank A to tank B labeled mixture 4 gal/min.

The third pipe connects tank A and B on the top of the tanks and has an arrow pointing from tank B to tank A and is labeled mixture 1 gal/min.

The fourth pipe connects the bottom of tank B to a point outside of the image, with an arrow pointing away from tank B that is labeled mixture 3 gal/min.

Assume that tank A contains 50 gallons of water in which 25 pounds of salt is dissolved. Suppose tank B contains 50 gallons of pure water. Liquid is pumped into and out of the tanks as indicated in the figure; the mixture exchanged between the two tanks and the liquid pumped out of tank B are assumed to be well stirred. We wish to construct a mathematical model that describes the number of pounds

x₁(t)

and

x₂(t)

of salt in tanks A and B, respectively, at time t.

This system is described by the system of equations

dx₁

−

x₁

x₂

dx₂

x₁

−

x₂

with initial conditions

x₁(0) = 25,

x₂(0) = 0.

What is the system of differential equations if, instead of pure water, a brine solution containing 5 pounds of salt per gallon is pumped into tank A?

dx₁

dx₂

Viewing Saved Work Revert to Last Response

6. –/3 points ZillDiffEQModAp12 5.1.025.MI. My Notes

This exercise will develop conceptual understanding.
A wealth of exercises provide modelling problems on a variety of applications, building students' skills of putting their learnings to use.

A mass weighing 4 pounds is attached to a spring whose constant is 2 lb/ft. The medium offers a damping force that is numerically equal to the instantaneous velocity. The mass is initially released from a point 1 foot above the equilibrium position with a downward velocity of 16 ft/s. Determine the time (in s) at which the mass passes through the equilibrium position. (Use

g = 32 ft/s²

for the acceleration due to gravity.)

Find the time (in s) after the mass passes through the equilibrium position at which the mass attains its extreme displacement from the equilibrium position.

What is the position (in ft) of the mass at this instant?

Need Help?

Viewing Saved Work Revert to Last Response

7. –/23 points ZillDiffEQModAp12 7.3.PJT.001. My Notes

Question Part

Points

Submissions Used

–/1

0/100

Total

–/23

This exercise will develop conceptual understanding.
Project questions give an opportunity to work on extended modelling examples from real life scenarios.

Project: Murder at the Mayfair Diner

Read "Project for Section 7.3: Murder at the Mayfair Diner" in your textbook and answer the questions below.

Question 1

Solve the equation below, which models the scenario in which Joe Wood is killed in the refrigerator. Use the fact that at 6:00 a.m.
(t = 0)
the core body temperature of the corpse was 85 degrees Fahrenheit and the temperature of the freezer
T_m
was 50 degrees Fahrenheit.

dT
dt
= k(T − T_m), t > 0

T(t) =

Now, use the solution above and the fact that at 6:30 a.m. the core body temperature of the corpse was 84 degrees Fahrenheit to find the value of k.

k =

Use these solutions to estimate the time of death (recall that normal living body temperature is 98.6 degrees Fahrenheit).

To estimate the time of death in this case we find t. Rounded to four decimal places, t = , which corresponds to approximately hours minutes before 6:00 a.m., which is
Question 2

Solve the differential equation below using Laplace transforms. Your solution
T(t)
will depend on both t and h. (Use the value of k found in Question 1.)

dT
dt
= k
T − T_m(t)

T(t) = 50 + 35e^kt + 20𝒰(t − h)
e^{k(t − h)}

T(t) = 50 + 35e^{k(t − h)} + 20𝒰(t − h)
1 − e^{k(t − h)}

T(t) = −50 + 120e^kt + 20𝒰(t − h)
e^{k(t − h)}

T(t) = −50 + 120e^kt + 20𝒰(t − h)
1 − e^{k(t − h)}

T(t) = 50 + 35e^kt + 20𝒰(t − h)
1 − e^{k(t − h)}

Question 3

Complete Daphne's table. (A computer algebra system is recommended.)

h	time body moved	time of death
12	6:00 p.m.
11	7:00 p.m.
10	8:00 p.m.
9	9:00 p.m.
8	10:00 p.m.
7	11:00 p.m.
6	12:00 a.m.
5	1:00 a.m.
4	2:00 a.m.
3	3:00 a.m.
2	4:00 a.m.

Explain why large values of h give the same time of death.

The large values of h all give the same time of death because these values of h are the t value we computed in Question 1, assuming that Joe was murdered in the refrigerator.

Question 4

Who does Daphne want to question and why?

Daphne wants to question the cook Shorty. The cook took a break around 10:30 p.m. and left the restaurant at 2:00 a.m. If Shorty moved the body when he left the restaurant then
h ≈ 4.
Our table then gives a time of death of about This is consistent with the cooks break ("Shorty took an unusually long break at 10:30 p.m.")

Twinkles didn't do it since she left no later than 6:00 p.m.

Similarly, Slim probably didn't do it since he left around 11:00 and our calculations indicate that if Joe was in the refrigerator at that time then he died around

It might be worth questioning Slim further (on the assumption that Joe didn't die immediately), but these calculations better indicate that Shorty is perpetrator.
Question 5

The process of temperature change in a dead body is known as algor mortis (rigor mortis is the process of body stiffening), and although it is not perfectly described by Newton's Law of Cooling, this topic is covered in most forensic medicine texts. In reality, the cooling of a dead body is determined by more than just Newton's Law. In particular, chemical processes in the body continue for several hours after death. These chemical processes generate heat, and thus a near constant body temperature may be maintained during this time before the exponential decay due to Newton's Law of Cooling begins.

A linear equation, known as the Glaister equation, is sometimes used to give a preliminary estimate of the time t since death. The Glaister equation is

t =
98.4 − T₀
1.5
,

where
T₀
is measured body temperature (98.4°F is used here for normal living body temperature instead of 98.6°F). Although we do not have all of the tools to derive this equation exactly (the 1.5 degrees per hour was determined experimentally), we can derive a similar equation via linear approximation.

(a)

Use the following equation with an initial condition of
T(0) = T₀
to compute the equation of the tangent line to the solution through the point
(0, T₀).
Do not use the values of
T_m
or k found in Question 1. Simply leave these as parameters.

dT
dt
= k(T − T_m), t > 0

T =

(b)

Using the equation found in part (a), let T = 98.4 and solve for t.

t =

Viewing Saved Work Revert to Last Response

8. 0/2 points | Previous Answers ZillDiffEQModAp12 6.1.003. My Notes

This exercise will address readiness gaps.
Power series are reviewed in depth in a dedicated section of the textbook and respective exercises.

Find the interval I and radius of convergence R for the given power series. (Enter your answer for interval of convergence using interval notation.)

∞

5ⁿ

xⁿ

n = 1

I	=
R	=	0

Need Help?

Viewing Saved Work Revert to Last Response

9. –/1 points ZillDiffEQModAp12 CR.9.005.MI. My Notes

This exercise will address readiness gaps.
Calculus Review exercises cover key tools that will be used in the course.

Evaluate the indefinite integral. (Use C for the constant of integration.)

(ln(x))³⁸

Need Help?

Viewing Saved Work Revert to Last Response

Home My Assignments

WebAssign

Welcome, demo@demo

Zill - Differential Equations with Modeling 12/e (Homework)

Current Score : 15 / 51

Due : Sunday, January 27, 2030 00:00 EST

Last Saved : n/a Saving... ()

Instructions

Assignment Submission

Assignment Scoring

Project: Murder at the Mayfair Diner

Question 1

Question 2

Question 3

Question 4

Question 5